
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конечные упорядоченные множества.
Порядковые типы ω, η, λ. Обратные типы. Будем говорить, что упорядоченное множество Ао имеет мощность m тогда и только тогда, когда запас данного множества есть множество мощности m, то есть когда Сходным образом множество Ао называется счетным, конечным или пустым, когда соответственно множество Ао счетно, конечно или пусто. Заметим еще, что упорядоченное множество мы называем равночисленным тогда и только тогда, когда их запасы равночисленны. Лемма 5.1. Любое конечное упорядоченное множество имеет первый элемент. Доказательство. Пусть натуральное число n – мощность упорядоченного множества Ао. (Доказательство по индукции). Если n=1, то первый элемент множества Ао есть его единственный элемент (Базис индукции). Допустим, что лемма верна для натурального числа k и что
Пусть а – произвольный элемент множества Ао. Обозначим через Ао, подмножество множества Ао, запас которого – разность множества А и одноэлементного множества {а}. Очевидно, что Значит, по индуктивному предположению существует первый элемент а1 множества Доказательство закончено. Теорема 5.1. Если конечные упорядоченные множества Ао и Во равночисленны, то данные множества подобны. Доказательство. Допустим, что Определим индуктивно конечную последовательность. (1) а1, а2, ….. аn. Пусть первым членом последовательности (1) будет первый элемент множества Ао. Существование такого элемента гарантирует лемма 5.1. Будем считать, что мы определил члены: (2) а1, а2, ….. аk, где k<n из последовательности (1). Обозначим через А1 разность множества А и запаса последовательности (2). Пусть аk+1 – первый элемент подмножества Таким способом, последовательность (1) полностью определена. Аналогично мы определяем последовательность (3) b1, b2, ……..,bn, Члены которой – элементы множества В.
Таким образом, R устанавливает подобие множеств Ао и Во. Из теоремы 5.1. следует: Следствие 5.1. Любое упорядоченное n – элементное множество подобно множеству всех натуральных чисел £ n, упорядоченных отношением «меньше».
Из теоремы 5.1. следует, что конечные и равночисленные упорядоченные множества имеют тот же самый порядковый тип. Эти типы будем обозначать символами, которыми мы обозначали натуральные числа. Так, например, порядковый тип пятиэлементного множества обозначим символом «5». Этот символ в соответствии с соглашениями предыдущего раздела (раздела общей теории множеств) одновременно обозначает мощность пятиэлементного множества. Эта нестрогость не грозит противоречием, потому что свойства порядковых типов и кардинальных чисел конечных множеств одинаковы. В частности, законы операций над порядковыми типами и кардинальными числами конечных множеств одинаковы. Таким образом, арифметику натуральных чисел мы можем строить как арифметику кардинальных чисел конечных множеств или же как арифметику порядковых типов конечных множеств. В качестве иллюстрации сделанных выше замечаний мы приводим следующую теорему: Теорема 5.2. Если m и n – порядковые типы конечных множеств, то (1) m+n=n+m (2) m×n=n×m Как выше было указано, сложение и умножение произвольных порядковых типов не коммутативно. Доказательство. Пусть (3) Очевидно, что множества Ао+Во и Во+Ао конечны и равночисленны. Данное замечание относится равным образом и к множествам Ао×Во Во×Ао. Отсюда из определений 3.3., 3.4 и формул (3) следуют формулы (1) и (2). Рассмотрим теперь более подробно множества, удовлетворяющие следующим трем условиям:
а) Упорядоченное множество Хо имеет первый элемент; b) Упорядоченное множество Хо не имеет последнего элемента; с) Любое сечение множества Хо есть скачок. Теорема 5.3. Если упорядоченные множества Ао и Во удовлетворяют условиям а)-с), то данные множества подобны. Доказательство. Определим индуктивно бесконечную последовательность. (1) а1, а2, а3, ….. Член а1 есть первый элемент множества Ао. Существование этого элемента гарантируется тем, что множество Ао удовлетворяет условию а). Допустим, что уже определены члены а1, а2, ……аk последовательности (1). Следующие эквивалентности определяют два подмножества упорядоченного множества Ао:
Из того, что множество Ао удовлетворяет условию b), следует, что множество Легко проверить, что упорядоченная пара Из того, что данное множество удовлетворяет условию с) следует, что множество Сходным образом мы определим бесконечную последовательность (2) b1, b2, b3……., члены которой – элементы множества Во. Определим еще отношение R. (3) Покажем прежде всего, что (4) Из (3) следует, что множества Dℓ(R) равно запасу последовательности (1). Очевидно также, что любой член этой последовательности есть элемент множества Ао. Для доказательства формулы (4) достаточно поэтому показать, что любой элемент множества Ао есть один из членов последовательности (1). Допустим – вопреки тому, что мы хотим доказать, - что некоторый элемент а множества Ао отличен от любого члена последовательности (1). Отсюда легко следует, что элемент а удовлетворяет одному из трех условий: a) b) g) Но случай a) невозможен, потому, что а1 – первый элемент множества Ао. Если бы имел место случай b), то – как легко видеть – элемент а не принадлежал бы ни одному из множеств Допустим теперь, что имеет место случай g). Следующие эквивалентности определяют два подмножества упорядоченного множества Ао:
Легко видеть, что пара Однако данное заключение противоречит допущению, что Ао удовлетворяет условию с). Поэтому случай g) также не может иметь места. Таким образом, формула (4) верна. Доказательство того, что Dр(R)=В аналогично. Доказательство того, что отношение R удовлетворяет остальным условиям I), сформулированным в доказательстве теоремы 5.1, сделать самостоятельно. Из того, что отношение R удовлетворяет этим условиям, и из D 2.4 следует: Ао@RВо. Отношение R устанавливает подобие упорядоченных множеств Ао и Во. Отсюда и из D 2.5 следует теорема. Определение 5.1. Очевидно, что множество áN,< ñ удовлетворяет условиям а) ¸ с). Отсюда: Следствие 5.2. Эта формула может играть роль определения порядкового типа w. Таким образом, любое упорядоченное множество, удовлетворяющее условиям а) ¸ с) счетно. Поэтому кардинальное число Àо может быть определено независимо от понятия натурального числа. Однако, если мы строим теорию множеств, не пользуясь понятием натурального числа, то мы должны принять аксиому, гарантирующую существование хотя бы одного счетного множества. Далее рассмотрим множества, удовлетворяющие условиям: а') упорядоченное множество Хо не имеет ни первого, ни последнего элемента; b') упорядоченное множество Хо счетно; с') упорядоченное множество Хо плотно. Теорема 5.4. Если упорядоченные множества Ао и Во удовлетворяют условиям а) ¸ с), то данные множества подобны. Доказательство. Из допущения, что множества Ао и Во удовлетворяют условию b'), и из теоремы 7.3 раздела I следует существование бесконечных последовательностей.
(1) а1, а2, а3…….. (2) b1, b2, b3…….. удовлетворяющих условиям: 1) запасы последовательностей (1) и (2)–соответственно множества А и В; 2) если i≠j, то аi≠аj и bi≠bj. Определим индуктивно бесконечную последовательность (3) Пусть член Допустим также, что для произвольных натуральных чисел m и n, не превосходящих k, имеет место соотношение: (4) am Очевидно, что член аk+1 последовательности (1) должен удовлетворять одному из условий: α) β) aj γ) Пусть в каждом из этих случаев член α') β') γ') Существование члена bℓ следует: 1) в случае α') и γ') из того, что множество B0 удовлетворяет условию а'). 2) в случае β') из того, что множество B0 удовлетворяет условию с'), и из соотношения (4). Очевидно, что соотношение (4) остается верным, когда m и n примут значение k+1. Таким образом данное соотношение (4) верно для всех членов последовательностей (1) и (3). Следующая эквивалентность определяет отношение a Покажем, что любой член последовательности (2), а потому и каждый элемент множества В является одним из членов последовательности (3). Временно будем полагать, что это неверно, и пусть bℓ - первый член последовательности (2), который не вошел в последовательность (3). Таким образом, каждый из членов b1,…, bℓ-1 совпадает с некоторым членом последовательности (3). Обозначим через Пусть k – наибольшее из чисел r1,…,rℓ-1. Допустим далее, что bℓ - удовлетворяет условию α') и что as – первый член последовательности (1), предшествующий в множестве А0 каждому из членов (5) a1,…, ak последовательности (1). Поэтому каждый из членов ak,…, aS-1 следует хотя бы за одним из членов (5). Значит aS предшествует каждому из членов a1,…, aS-1. Из того, что соотношение (4) выполняется для всех членов последовательностей (1) и (3), заключаем: Каждый из членов Поэтому член bℓ предшествует каждому из членов Отсюда и из определения последовательности (3) следует, что bℓ=
Аналогичные доказательства того, что bℓ является одним из членов последовательности (3) в случае, когда данный член удовлетворяет условиям β' или γ' сделать самостоятельно. Из предшествующего рассмотрения уже легко следует, что DP(R)=B. Установление того, что имеют место остальные из условий I, сформулированные в доказательстве теоремы 5.1, не представляет трудностей. Таким образом, отношение R устанавливает подобие множеств A0 и B0. Отсюда уже следует теорема 5.4. Доказанная теорема позволяет принять следующее определение: Определение 5.2. η = Ā0 Очевидно, что множество áB,<ñ удовлетворяет условиям a ') – c '). (B - множество рациональных чисел.)
η= áB,<ñ. Эта формула может служить определением порядкового типа η. Теперь рассмотрим множества, удовлетворяющие условиям:
b"). Упорядоченное множество X0 непрерывно. c").
Словесно условие c" формулируется так: существует счетное подмножество W0 множества X0, такое, что для любых двух (различных) элементов множества X0 существует средний элемент, принадлежащий подмножеству W0. Теорема 5.5. Если упорядоченные множества A 0 и B 0 удовлетворяют условиям a ") – c "), то данные множества подобны. Доказательство (сокращенное). Пусть
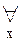 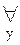 [ x [ x 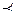 A y A y 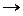 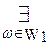 (x (x 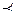 A A 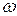 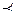 A y)]. A y)].
Существование таких подмножеств гарантируется допущением, что множества A0 и B0 удовлетворяют условию c"). Легко выявить, что множества Пусть отношение S устанавливает подобие множеств Пусть x будет произвольным элементом множества A0. Обозначим через
Легко видеть, что упорядоченная пара á Обозначим через C0 произведение множеств Обозначим еще через Поэтому и в множестве S (C), которое есть подмножество множества B0, также нет последнего элемента. Отсюда уже легко следует, что множество Отсюда и из допущения, что множество B0 удовлетворяет условию b", следует существование первого элемента множества
(2) Dℓ(R)=A. (3) R Сходным образом можно привести в соответствие произвольному элементу y множества B0 точно один элемент множества A0. Легко видеть, что приведенные в данное соответствие элементы x и y находятся в отношении R. Отсюда: (4) DP(R)=A. (5) Из формул (3) и (5) следует, что R Таким образом, множества A0 и B0 подобны.
Определение 5.3. Легко видеть, что множество á Отсюда:
Эта формула может играть роль определения порядкового типа Среди сечений данного упорядоченного множества A0, которые не относятся ни к скачкам, ни к пробелам, имеются пары сечений, различающиеся лишь тем, что некоторый элемент a множества A0 есть последний элемент нижнего класса одного из этих сечений и одновременно первый элемент верхнего класса другого сечения. Такими сечениями, например, являются сечения множества á Устраним из множества всех сечений множества A0 те принадлежащие к только что охарактеризованным парам сечения, в которых нижний класс имеет последний элемент. Полученное таким путем множество будем называть множеством всех собственных сечений множества A0. Из этого определения и определения 4.4а следует: Следствие 5.5. Ни в одном из сечений, принадлежащих множеству собственных сечений плотного множества, нижний класс не имеет последнего элемента. Легко видеть, что отношение, определяемое формулой (II) á упорядочивает множество всех собственных сечений множества A 0. Лемма 5.2. Если упорядоченное множество A 0 плотно, то множество U 0 всех его собственных сечений, упорядоченное отношением Доказательство. Нужно показать, что ни одно сечение á Очевидно, что á Отсюда и из формулы II следует, что Поэтому существует такой элемент a множества A, что (1) Из следствия 5.5. мы выводим также, что существует элемент a 1, удовлетворяющий условию (2) Следующие формулы определяют подмножества множества A0: (3) x x Очевидно, что упорядоченная пара á Данное заключение противоречит допущению, что упорядоченная пара á Таким образом данное множество плотно. Теорема 5.6. Если упорядоченное множество А0 плотно, то множество U 0 всех его собственных сечений, упорядоченных отношением R, которое определяется условием II, непрерывно. Доказательство. Пусть упорядоченная пара á (1) x (2) y Легко видеть, что упорядоченная пара á á Отсюда и из условия II следует Из леммы 5.2 следует, что ни одно сечение множества U0 не есть скачок. Таким образом, данное множество непрерывно. В теории действительных чисел Дедекинда, которая упоминалась в начале предыдущего параграфа, действительные числа определяются как собственные сечения множества рациональных чисел, упорядоченного отношением «меньше». Условие II определяет отношение «меньше» для так понимаемых действительных чисел.
Определение 5.4. β = α*
α=<X,R>
(<X,R>)*=<X,R-1>. Порядковый тип α* называется обратным к порядковому типу α. Если α - порядковый тип множества X, упорядоченного отношением R, то α* - порядковый тип множества X, упорядоченного отношением, обратным к R, или конверсией отношения R. Из определения 5.4. и следствия 5.2. следует, что w*=á Таким образом, порядковый тип w* - это порядковый тип упорядоченных множеств, которые не имеют первого элемента, имеют последний элемент и каждое сечение которых есть скачок. Как легко заметить, это – порядковый тип отрицательных целых чисел, упорядоченных отношением á. На этом примере мы видим, что тип α* может не совпадать с типом α. Однако в некоторых случаях тип, обратный порядковому типу α, тождествен типу α. Так, например, из теоремы 5.1. следует, что n*=n (где n – порядковый тип конечного множества); Из теорем 5.4. и 5.5. следует, что (w*+w)*=w*+w. Порядковый тип w*+w – это порядковый тип множества целых чисел, упорядоченных отношением Упорядоченные множества данного типа не имеют ни первого, ни последнего элемента, а любое их сечение есть скачок.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 52; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.233.72 (0.178 с.) |
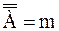 .
.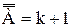
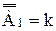 .
.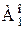 . Первым элементом множества Ао будет тот элемент из пары а,а1, который предшествует другому.
. Первым элементом множества Ао будет тот элемент из пары а,а1, который предшествует другому.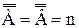 ,
, 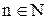 .
.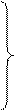 Пусть отношение R имеет место между членами последовательности (1) и (3) тогда, и только тогда, когда индексы данных членов равны. Легко показать, что
Пусть отношение R имеет место между членами последовательности (1) и (3) тогда, и только тогда, когда индексы данных членов равны. Легко показать, что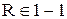
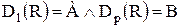 I – см. стр. 82
I – см. стр. 82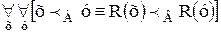
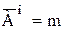 ,
, 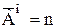 ,
, 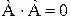 .
.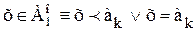
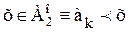
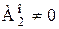 .
.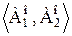 есть сечение множества Ао.
есть сечение множества Ао.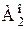 имеет первый элемент. Пусть этот элемент будет (k+1)-м членом последовательности (1).
имеет первый элемент. Пусть этот элемент будет (k+1)-м членом последовательности (1).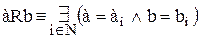
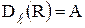
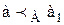
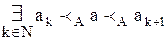
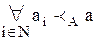
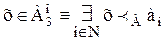 ;
;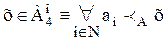
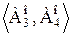 есть сечение множества Ао, причем множество
есть сечение множества Ао, причем множество 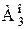 не имеет последнего элемента.
не имеет последнего элемента.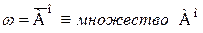 удовлетворяет условиям а) ¸ с).
удовлетворяет условиям а) ¸ с).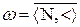
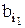 ,
, 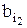 ,
, 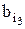 ,…
,…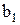 . Допустим, что члены
. Допустим, что члены 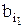 ,
, 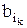 уже определены.
уже определены.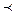 A an ≡
A an ≡ 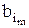
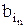 .
.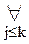 аk+1
аk+1 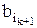 последовательности (3) равен члену bℓ - первому члену последовательности (2), которая удовлетворяет соответственно условиям:
последовательности (3) равен члену bℓ - первому члену последовательности (2), которая удовлетворяет соответственно условиям: ;
;
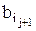 ;
; :
: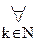 (a=ak
(a=ak 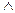 b=
b= 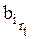 член этой последовательности, удовлетворяющий условию:
член этой последовательности, удовлетворяющий условию: 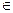 {1,…, ℓ-1}.
{1,…, ℓ-1}.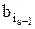 следует в множестве B0 хотя бы за одним из членов
следует в множестве B0 хотя бы за одним из членов 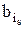 .
.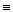 множество A 0 удовлетворяет условиям a ') – c ').
множество A 0 удовлетворяет условиям a ') – c '). Следствие 5.3.
Следствие 5.3.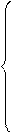 a"). Упорядоченное множество X0 не имеет ни первого, ни последнего элемента.
a"). Упорядоченное множество X0 не имеет ни первого, ни последнего элемента.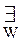 {W0
{W0 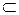 X0
X0 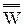 =
= 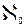
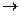
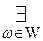 (x
(x 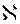 0 – алеф 0.
0 – алеф 0.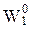 и
и 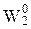 - соответственно счетные подмножества множеств A0 и B0, удовлетворяющие условиям:
- соответственно счетные подмножества множеств A0 и B0, удовлетворяющие условиям: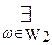 (x
(x 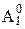 подмножество множества A0, которому принадлежат все элементы данного множества, предшествующие в нем элементу x, через
подмножество множества A0, которому принадлежат все элементы данного множества, предшествующие в нем элементу x, через 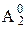 - подмножество множества A0, которому принадлежат все остальные элементы данного множества.
- подмножество множества A0, которому принадлежат все остальные элементы данного множества.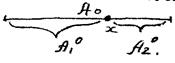
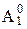 ,
, 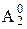 ñ есть сечение множества A0 и что x – первый элемент множества
ñ есть сечение множества A0 и что x – первый элемент множества 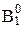 – подмножество множества B0, такое, что
– подмножество множества B0, такое, что 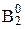 подмножество множества B0, такое, что
подмножество множества B0, такое, что 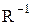
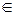 1-1. Проверку того, что выполняется также третье из условий I, сформулированных в доказательстве теоремы 5.1, сделать самим.
1-1. Проверку того, что выполняется также третье из условий I, сформулированных в доказательстве теоремы 5.1, сделать самим. Доказанная теорема позволяет принять следующее определение:
Доказанная теорема позволяет принять следующее определение: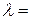 A0
A0 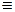 множество A 0 удовлетворяет условиям a ") – c ").
множество A 0 удовлетворяет условиям a ") – c ").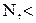 ñ удовлетворяет условиям a") – c"), причем множество W, о котором говорится в условии c"), есть множество B всех рациональных чисел.
ñ удовлетворяет условиям a") – c"), причем множество W, о котором говорится в условии c"), есть множество B всех рациональных чисел. Следствие 5.4.
Следствие 5.4. 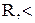 ñ (R – действительные числа)
ñ (R – действительные числа)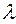 .
.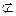
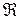 , которое определяется формулой II, также плотно.
, которое определяется формулой II, также плотно.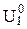 ,B
,B 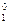 ñ множества U0 не есть скачок. Пусть – вопреки тому, что требуется доказать,- сечение á
ñ множества U0 не есть скачок. Пусть – вопреки тому, что требуется доказать,- сечение á 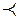 U á
U á 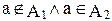 .
.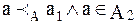 .
.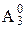
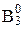
 x = a1.
x = a1.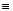
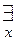
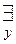 (áX0,Y0ñ)
(áX0,Y0ñ) 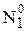
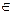
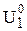 . Из допущения, что сечение á
. Из допущения, что сечение á 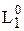 ñ есть пробел, следует существование такого сечения á
ñ есть пробел, следует существование такого сечения á 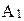
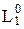 . Поэтому ни одно сечение класса U0 не есть пробел.
. Поэтому ни одно сечение класса U0 не есть пробел.
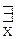
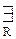 (α=<X,R>
(α=<X,R> 

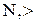 ñ.
ñ.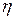 *=
*= 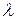 *=
*= 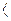 .
.


