
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Г. Генцен, «Исследование логических выводов» в сб. «Математическая теория логического вывода», пер. под ред. А.В. Идельсона, Г.Е. Минца, изд-во «Наука», М., 1987.
Эта работа является классической и служит теоретической базой построения многих алгорифмов машинного доказательства теорем В этой работе описаны две формализации исчисления предикатов. Первая – формализация общеупотребительного в математике метода построения логических выводов с введением допущений (формализация «натурального» типа). Вторая – формализация, особенно удобная для использования самого аппарата логического вывода (формализация «логического» типа). Основным результатом работы является теорема об устранимости правила «сжатия» в формализации логического типа. Эта теорема служила и служит отправным пунктом для многих исследований по теории логического вывода, а также теоретической базой для построения многих алгоритмов машинного доказательства теории.
Обзор работы. Исследования в данной работе относятся к области логики «узкого исчисления предикатов». Эта логика охватывает такие выводы, которые постоянно применяются во всех разделах математики. К ним могут присоединяться ещё аксиомы и правила вывода, которые можно причислить собственно к отдельным разделам математики, таковы, например, в арифметике аксиомы натуральных чисел, сложения, умножения и возведения в степень, а также правило полной индукции; в геометрии – геометрические аксиомы. Наряду с классической логикой в работе рассматривается и интуиционистская логика в том виде, как она формализована, например, Гейтингом. Настоящие исследования классической и интуиционистской логики предикатов распадаются, по существу, на две лишь слабо связанные друг с другом части. 1. Исходная точка зрения автора заключается в следующем: формализация логических выводов, проведённая, в частности, Фреге, Расселом и Гилбертом, очень далёких от тех способов рассуждений, которые применяются в действительности при математических доказательствах. Автор хотел, прежде всего, построить такой формализм, который был бы как можно ближе к применяющимся в действительности рассуждениям. Так возникло «исчисление натуральных выводов» («NJ» – для интуиционистской логики предикатов, «NK» – для классической логики предикатов). Далее устанавливается, что исчисление обладает некоторыми особыми свойствами и что отвергаемый интуиционистский «закон исключённого третьего» занимает по отношению к этим свойствам особое место.
Исчисление натуральных выводов рассматривается в разделе 2 данной работы. 2. Более тщательное исследование особых свойств натурального исчисления привело автора к установлению очень общей теоремы, которую он называет «основной теоремой». В основной теореме утверждается, что каждое чисто логическое доказательство может быть приведено к некоторой определённой, хотя и неоднозначно, нормальной форме. Наиболее существенное свойство такого нормального доказательства можно выразить так: оно не содержит окольных путей. В него не вводится никаких понятий, кроме тех, которые содержатся в конечном результате и поэтому с необходимостью должны быть использованы для получения этого результата. Основная теорема справедлива как для классической, так и для интуиционистской логики предикатов. Для того чтобы сформулировать её в соответствующей форме, пришлось ввести особое, подходящее для этого целей логическое исчисление. Натуральное исчисление оказалось непригодным для этих целей.
Раздел I. Обозначения. Понятиям «объект», «функция «, «предикат», «высказывание», «теорема», «аксиома», «доказательство», «вывод» и т.д. в логике и математике при их формализации сопоставляются определённые знаки и комбинации этих знаков. Мы их делим на: 1) знаки, 2) выражения – конечные последовательности знаков, 3) фигуры – каким - либо образом упорядоченные конечные множества знаков. Знаки являются частным случаем выражений и фигур, выражения – частным случаем фигур. В дальнейшем будем рассматривать знаки, выражения и фигуры следующих видов.
Знаки. Знаки делятся на знаки для постоянных и для переменных.
Знаки для постоянных. Знаки для постоянных объектов: 1, 2, 3, … Знаки для постоянных функций: +, –, ∙. Знаки для постоянных высказываний: Υ («истинное высказывание»), L («ложное высказывание»). Знаки для постоянных предикатов: =, <. Логические знаки: & «и», Ú «или», É «из … следует», ÉÌ «эквивалентно» (º),
Вспомогательные знаки: (,), ®.
Переменные. Предметные переменные: а) свободные: a, b, c, …, m. б) связанные: n, …, x, y, z. Переменные высказывания: A, B, C, … Необходимо иметь в распоряжении сколь угодно много переменных; когда алфавит оказывается недостаточным, мы приписываем к буквам цифровые индексы, например, a7, c3.
1.3. Готические и греческие буквы служат нам в качестве «информационных знаков» и являются, следовательно, не знаками формализованной логики, а переменными в наших рассуждениях о ней. Их значения будут разъясняться там, где они применяются.
Выражения. 2.1. Понятие высказывательного выражения, называемого кратко формулой (определяется индуктивно). Понятие формулы употребляется нередко и в более общем смысле; определяемый в дальнейшем частный случай мы могли бы поэтому называть «чистой логической формулой».
2.1.1. Знак для постоянного высказывания есть формула. Это знаки ¡ и L. Переменное высказывание с некоторым числом (возможно, равным нулю) следующих за ним свободных предметных переменных есть формула. Например, Abab. Предметные переменные называются аргументами переменного высказывания. Формулы описанных двух видов мы называем также элементарными формулами.
2.1.2. Если U является формулой, то U тоже является формулой. Если U и В являются формулами, то (U&В), (UÚВ), (UÉВ) тоже являются формулами. (Знак ÉÌ в нашем исследовании не вводится; это излишне, т.к. UÉÌВ может рассматриваться как сокращение для (UÉВ)&(ВÌU)).
2.1.3. Из формулы, в которую не входит связанная предметная переменная х, возникает новая формула, если перед ней ставится "х или $х, причем одновременно можно заменить на х некоторую входящую в формулу свободную предметную переменную на некоторых местах.
2.1.4. С помощью скобок следует обеспечивать возможность однозначно видеть построенные формулы. Пример формулы: $x((( Введя специальные соглашения, можно опускать скобки; мы не будем прибегать к этому (за исключением случая, описанного в пункте 2.4), т.к. не придется выписывать много формул.
2.2. Степенью формулы будем называть число входящих в нее логических знаков (элементарная формула имеет, таким образом, степень 0). Внешним знаком формулы, не являющейся элементарной, будем называть тот логический знак, который был введен последним при построении формулы в соответствии с 2.1.2 и 2.1.3. Подформулами данной формулы будем называть те формулы, которые строятся в процессе построения данной формулы в соответствии с 2.1.2 и 2.1.3, включая и саму данную формулу. Пример. Подформулами формулы A&"xBxa являются: A "xBxa A&"xBxa а также все формулы виды Baa, где посредством a обозначена любая свободная предметная переменная (например, a может и совпадать с a). Степень A&"xBxa равна 2 (&,"), внешним знаком ее является a.
2.3. Понятие секвенции. Секвенция есть выражение вида U1, …, Um ® В1, …, Вn где U1, …, Um, В1, …, Вn – произвольные формулы. Знак ® и запятые являются не логическими, а разделительными знаками. Знак «®» читается: «приводит к».
Формулы U1, …, Um образуют антецедент, формулы В1, …, Вn – сукцедент секвенции. Оба выражения могут быть пустыми. Секвенция обладает свойствами, сходными со свойствами логического следования.
2.4. Секвенция U1, …, Um ® В1, …, Вn содержательно означает в точности то же самое, что формула (U1&…&Um)É(В1Ú…ÚВn) Если антецедент пуст, то подразумевается формула В1, …, Вn. Если сукцедент пуст, то секвенция означает то же самое, что формула
Если и антецедент и сукцедент оба пусты, то секвенция означает то же, что L, т.е. ложное высказывание. Обратно, для каждой данной формулы существует эквивалентная секвенция, например та, антецедент которой пуст, а сукцедент состоит из одной данной формулы. Формулы, из которых состоит некоторая секвенция, будем называть S-формулами (т.е. секвенциальными формулами), выражая этим ту мысль, что мы подразумеваем не формулу как таковую, а формулу, связанную с ее листом в секвенции. Так, например, утверждение: «Данная формула входит в данную секвенцию в нескольких местах в качестве S-формулы» можно выразить следующим образом: «Несколько различных (что должно означать: стоящих на различных местах в секвенции) S-формул являются формально равными».
Фигуры.
Мы употребили фигуры заключения и фигуры доказательства. Они состоят из формул или из секвенций; мы будем говорить в дальнейшем лишь о формулах, но все сказанное справедливо и для секвенций, надо лишь слово «формула» заменить везде словом «секвенция».
3.1. Фигуру заключения можно записать в виде
где U1, …, U U1, …, U В - нижней формулой фигуры заключения. (Совершенно аналогично надо понимать термины: верхняя секвенция и нижняя секвенция фигуры заключения, состоящей из секвенций). Мы будем рассматривать лишь частные виды фигур заключения, которые будут введены в отдельных исчислениях.
3.2. Фигура доказательства, называемая кратко выводом, состоит из некоторого числа формул (по меньшей мере из одной формулы), которые образуют между собой фигуры заключения следующим образом: каждая формула является нижней формулой не более, чем одной фигуры заключения; каждая формула, кроме одной конечной формулы, является верхней формулой по крайней мере одной фигуры заключения;
совокупность фигур заключения не содержит кругов, т.е. формулы, входящие в вывод, не образуют циклов (рядов, в которых первый член следует за последним, если считать, что нижняя формула каждой из фигур заключения следует за каждой из верхних формул этой фигуры заключения).
3.3. Исходными формулами вывода называются такие формулы вывода, которые не являются нижними формулами никаких фигур заключения. Вывод называется древовидным, если все его формулы являются верхними формулами не более, чем одной фигуры заключения. Отсюда следует, что все формулы, за исключением конечной формулы, являются верхними формулами в точности одной фигуры заключения. Мы будем рассматривать только древовидные выводы. Формулы, из которых, в соответствии с определением, состоит вывод, мы называем H-формулами (т.е. формулами вывода (Herℓeitung – вывод)), выражая этим ту мысль, что мы подразумеваем не формулу как таковую, а формулу, связанную с ее местом в выводе. Т.е. иными словами H-формула – это вхождение формулы в вывод. В этом смысле мы употребляем выражения: «Формула входит в вывод в качестве H-формулы», «Две различные (т.е. стоящие на разных местах в выводе) H-формулы формально равны, т.е. равны одной и той же формуле». Т.о., выражение «U является той же H-формулой, что и В» означает, что U и В не только являются одинаковыми формулами, но и, кроме того, занимают одно и то же место в выводе. Говоря о совпадении формул безотносительно к занимаемым ими местам, мы употребляем слова «формально равные». Для предметной переменной мы не будем вводить никакого особого наименования, связывающего ее с местом, на котором она стоит в формуле. Например, мы говорим: «Одна и та же предметная переменная входит в две различные H-формулы».
3.4. Фигуры заключения, входящие с вывод, мы называем H-фигурами заключения. S-формулы H-секвенций некоторого вывода, состоящего из секвенций, мы называем H-S-формулами (т.е. секвенциальными формулами вывода).
3.5. Нитью в данном выводе мы называем (следуя Гильберту) любую последовательность H-формул этого вывода, удовлетворяющую следующим 3 условиям: 1) первая формула этой последовательности является исходной формулой; 2) последняя формула этой последовательности является конечной формулой; 3) каждая из формул этой последовательности, кроме последней, является верхней формулой той H-фигуры заключения, нижняя формула которой непосредственно следует за ней в нити. Мы говорим: «Данная H-формула стоит выше (соответственно ниже) другой данной H-формулы», когда существует нить, в которой первая предшествует (соответственно следует за) второй. При этом мы подразумеваем, что вывод записан в виде древовидной фигуры с исходными формулами наверху и колесной формулой внизу. Далее, мы говорим: «Данная H-фигура заключения стоит выше (соответственно, ниже) данной H-фигуры», если все формулы этой H-фигуры заключения стоят выше (соответственно, ниже) данной H-формулы.
Вывод с конечной формулой U мы будем называть также «выводом формулы U». Исходные формулы некоторого вывода могут быть основными формулами или допущениями, о сущности которых мы будем говорить подобнее при описании отдельных исчислений.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.044 с.) |
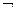 «не», " «для всех», $ «существуют». Мы допускаем также следующие наименования: и-знак, или-знак, знак следования, знак эквивалентности, знак отрицания, знак всеобщности, знак существования.
«не», " «для всех», $ «существуют». Мы допускаем также следующие наименования: и-знак, или-знак, знак следования, знак эквивалентности, знак отрицания, знак всеобщности, знак существования. (
(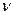 ³1),
³1),


