
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определим, входят ли полученные значения в область допустимых значений.
Для этого, установим, найдутся ли такие целые значения n, m, при которых:
Ответ:
Пример 54. Решите уравнение Решение
Преобразуем уравнение:
получим:
Ответ:
Пример 55. Решите уравнение
Решение
Преобразуем уравнение:
Преобразуем уравнение, применяя тождество:
Ответ:
Пример 56. Решите уравнение
Решение Область определения: Преобразуем уравнение:
Преобразуем уравнение, применяя тождество
Пусть Преобразуем уравнение:
Определим, какие из значений полученных переменных входят в область допустимых значений.
Ответ:
Пример 57. Решите уравнение
Решение
Преобразуем уравнение, применяя тождество
Пусть
Ответ:
Задание 2
Решите уравнения. 58. 60. 62. 64. 66. 68. 70. 71. 73. 75.
3. Уравнения, однородные относительно
Определение. Рассмотрим уравнение вида
где
Ясно, что если
Если же При Итак, при
которое, подстановкой
1. Однородные уравнения с показателем однородности 1. При Если откуда
Пример 7 6. Решите уравнение
Решение Это уравнение однородное первой степени Ответ:
Пример 7 7. При
Решение
Если Если
Пример 7 8. Решите уравнение
Решение
Это уравнение однородное второй степени. Разделим обе чести уравнения на
Ответ:
3. К уравнению вида (1) сводится уравнение
Для этого достаточно воспользоваться тождеством
В частности, уравнение
Пример 7 9. Решите уравнение
Решение
Преобразуем уравнение к однородному:
Разделим обе части уравнения на
Ответ:
Пример 8 0. Решите уравнение
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:
Пусть
Ответ:
Пример 81. Решите уравнение
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:
Получили однородное уравнение: Пусть
Ответ:
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 36; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.98.71 (0.044 с.) |
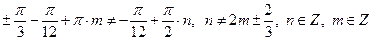 . Таких целых значений n и m нет, т. е. значения
. Таких целых значений n и m нет, т. е. значения 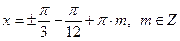 входят в область допустимых значений.
входят в область допустимых значений. .
.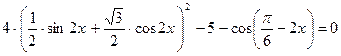 ,
, ,
,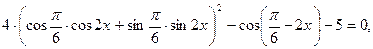
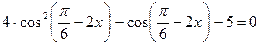 . Пусть
. Пусть 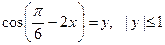 ,
, .
. .
. .
. .
. ,
,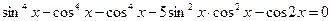 ,
,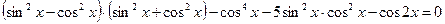 ,
, .
.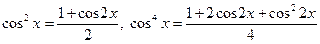 , а также тождество
, а также тождество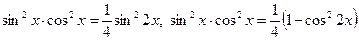 , получим уравнение:
, получим уравнение: ,
, ,
,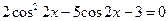 . Пусть
. Пусть 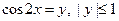 , получим:
, получим: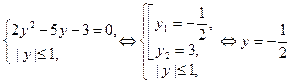 .
.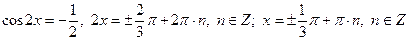 .
.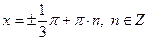 .
. .
. .
. .
.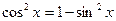 , получим уравнение:
, получим уравнение: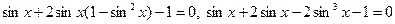 или
или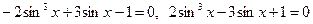 .
. , тогда получим уравнение:
, тогда получим уравнение:  . Нетрудно заметить, что y = 1 является корнем уравнения: при y = 1 получим:
. Нетрудно заметить, что y = 1 является корнем уравнения: при y = 1 получим: 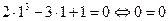 , значит, его левая часть можно разложить на множители, одним из которых является y - 1.
, значит, его левая часть можно разложить на множители, одним из которых является y - 1.

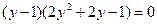
 ,
, .
.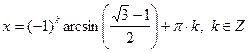 входит в о. д. з.
входит в о. д. з.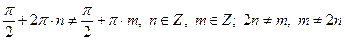 - это значит, что
- это значит, что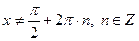 или
или  не входит в область допустимых значений.
не входит в область допустимых значений.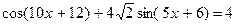 .
.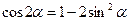 , в котором положим
, в котором положим 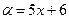 , тогда
, тогда 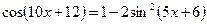 , получим уравнение:
, получим уравнение: .
.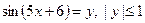 , получим
, получим .
.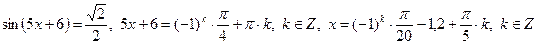 .
.
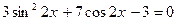 . 59.
. 59. 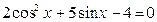 .
.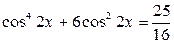 . 61.
. 61.  .
. . 63.
. 63. 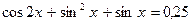 .
.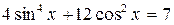 . 65.
. 65.  .
. . 67.
. 67.  .
. . 69.
. 69. 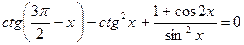 .
.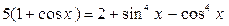 .
.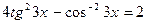 . 72.
. 72. 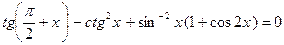 .
. . 74.
. 74.  .
.
 и
и 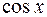

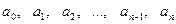 - действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно
- действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно 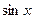 и
и  , а число n называется показателем однородности.
, а число n называется показателем однородности.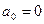 , то уравнение примет вид:
, то уравнение примет вид: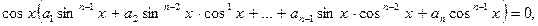 решениями которого являются значения x, при которых
решениями которого являются значения x, при которых  , т. е. числа
, т. е. числа 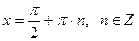 . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.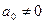 , то эти числа не являются корнями уравнения (1).
, то эти числа не являются корнями уравнения (1). получим:
получим: 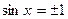 и левая часть уравнения (1) принимает значение
и левая часть уравнения (1) принимает значение 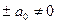 .
.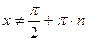 и
и 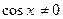 , поэтому можно разделить обе части уравнения на
, поэтому можно разделить обе части уравнения на  . В результате получаем уравнение:
. В результате получаем уравнение: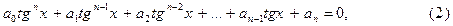
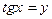 легко сводится к алгебраическому:
легко сводится к алгебраическому: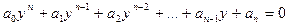 .
. имеем уравнение
имеем уравнение  .
. , то это уравнение равносильно уравнению
, то это уравнение равносильно уравнению  ,
, 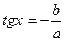 ,
, .
. .
.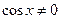 . Разделим обе его части на
. Разделим обе его части на 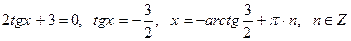 .
.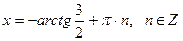 .
.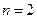 получим однородное уравнение вида
получим однородное уравнение вида .
. , получим уравнение
, получим уравнение 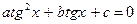 , которое подстановкой
, которое подстановкой  . Если
. Если  , то уравнение имеет действительные корни
, то уравнение имеет действительные корни  . Исходное уравнение будет иметь две группы решений:
. Исходное уравнение будет иметь две группы решений:  .
.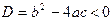 , то уравнение не имеет решений.
, то уравнение не имеет решений.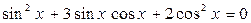 .
. . Пусть
. Пусть 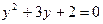 ,
,  ,
,  .
.  .
. .
.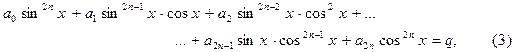
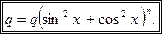
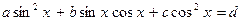 сводится к однородному, если заменить d на
сводится к однородному, если заменить d на 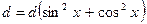 , тогда получим равносильное уравнение:
, тогда получим равносильное уравнение: 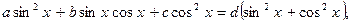
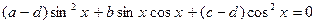 .
.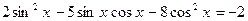 .
.
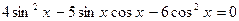 .
. , получим уравнение:
, получим уравнение: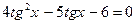 . Пусть
. Пусть  .
. .
.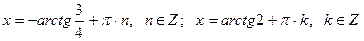 .
. .
. ,
,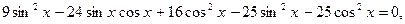
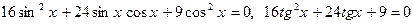 .
.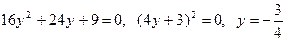 .
. .
.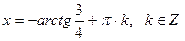 .
. .
. ,
,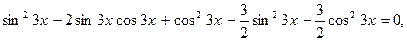
 .
. .
. ,
, ,
, .
. ,
, 


