
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод разложения на множителиСтр 1 из 8Следующая ⇒
Уравнений
Содержание
Тригонометрические уравнения. 4 1. Метод разложения на множители. 4 Задание 1. 18 2. Метод замены переменных и сведение к алгебраическим уравнениям 18 2.1. Применение формул двойного и половинного аргумента. 21 2.2. Применение формул приведения. 26 Задание 2. 30 3. Уравнения, однородные относительно 3.1. Применение формул приведения. 34 Задание 3. 37 Задание 4. 40 4. Метод замены переменных. 41 4.1. Замена Задание 5. 45 4.2. Замена 4.3. Случаи, когда в уравнении не содержится 4.4. Случаи, когда аргументы кратны 2x и x. 49 Задание 6. 51 4.5. Замена Задание 7. 58 5. Метод оценки левой и правой частей уравнения. 59 Задание 8. 63 6. Введение вспомогательного аргумента. 64 Задание 9. 67 7. Системы тригонометрических уравнений. 68 Задание 10. 70 Задание 11. 72 Ответы.. 73 К заданию 1. 73 К заданию 2. 73 К заданию 3. 73 К заданию 5. 73 К заданию 6. 74 К заданию 7. 74 К заданию 9. 74
Метод разложения на множители
Пример 1. Решите уравнение
Решение
Преобразуем уравнение. Применим формулу:
Получим уравнение: Это уравнение решим разложением на множители: Получим совокупность уравнений:
Ответ:
Пример 2. Решите уравнение
Решение Преобразуем уравнение:
Ответ:
Пример 3. Решите уравнение
Решение
Преобразуем уравнение. Применим формулы:
Получим уравнение:
Получим совокупность двух уравнений: (1) Уравнение (1) Разделим обе части уравнения (1) на Решим второе уравнение:
Ответ:
Пример 4. Решите уравнение
Решение
Преобразуем уравнение. Применим формулы:
Полученное уравнение равносильно совокупности уравнений:
Объединим полученные решения, если это возможно. Попробуем выработать общие принципы для объединения нескольких решений в одно.
Объединим два последних решения в одно: Далее, найдем общие решения
Ответ:
Пример 5. Решите уравнение
Решение
Преобразуем уравнение
Ответ:
Пример 6. Решите уравнение
Решение
Преобразуем уравнение, для этого прибавим к левой части уравнения и вычтем, чтобы выражение не изменилось, произведение
Ответ:
Пример 7. Решите уравнение
Решение
Левая часть этого уравнения представляет собой однородное выражение относительно Для преобразования уравнения в однородное, правую часть представим в виде:
Полученное уравнение равносильно совокупности двух уравнений:
Решая первое уравнение, находим: Второе уравнение является однородным первой степени, Если допустить, что
Ответ:
Пример 8. Решите уравнение
Решение Область допустимых значений переменной: Преобразуем уравнение:
Это уравнение равносильно совокупности двух уравнений:
Решение Преобразуем разность синусов
С учетом этого преобразования, уравнение примет вид
Ответ: Пример 10. Решить уравнение
Решение
Преобразуем уравнение:
Получим совокупность уравнений:
Ответ:
Пример 11. Решить уравнение
Решение Преобразуем уравнение, используя формулу
Полученное уравнение равносильно совокупности уравнений:
Ответ:
Пример 12. Решить уравнение
Решение Преобразуем уравнение:
Полученное уравнение равносильно совокупности уравнений:
Второе уравнение совокупности Первое уравнение решим как однородное. Разделим обе его части на
Ответ:
Пример 13. Решите уравнение
Решение
Преобразуем уравнение:
Это уравнение равносильно совокупности уравнений:
Ответ:
Пример 13. Решить уравнение
Решение
Преобразуем уравнение: Учитывая, что cosx функция четная, получим: Уравнение примет вид: Это уравнение равносильно совокупности уравнений:
Ответ:
Пример 15. Решите уравнение
Решение
Преобразуем уравнение, применяя тождество понижения порядка
Ответ:
Пример 16. Решите уравнение
Решение Преобразуем произведение функций в сумму, получим
Ответ: Пример 17. Решите уравнение
Решение
Преобразуем уравнение, применяя формулы приведения:
Ответ:
Пример 18. Решите уравнение
Решение
Область допустимых значений: Преобразуем уравнение, заменив 1 на
Отсюда находим
Задание 1 Решите уравнения 27. 29. 30. 32. 34. 36.
Задание 2
Решите уравнения. 58. 60. 62. 64. 66. 68. 70. 71. 73. 75.
3. Уравнения, однородные относительно
Определение. Рассмотрим уравнение вида
где
Ясно, что если
Если же При Итак, при
которое, подстановкой
1. Однородные уравнения с показателем однородности 1. При Если откуда
Пример 7 6. Решите уравнение
Решение Это уравнение однородное первой степени Ответ:
Пример 7 7. При
Решение
Если
Если
Пример 7 8. Решите уравнение
Решение
Это уравнение однородное второй степени. Разделим обе чести уравнения на
Ответ:
3. К уравнению вида (1) сводится уравнение
Для этого достаточно воспользоваться тождеством
В частности, уравнение
Пример 7 9. Решите уравнение
Решение
Преобразуем уравнение к однородному:
Разделим обе части уравнения на
Ответ:
Пример 8 0. Решите уравнение
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:
Пусть
Ответ:
Пример 81. Решите уравнение
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:
Получили однородное уравнение: Пусть
Ответ: Решение
Преобразуем уравнение: После приведения подобных слагаемых получим однородное уравнение третьей степени относительно sinx и cosx: Разделим обе части уравнения на Пусть tgx = y, тогда
Ответ:
Пример 8 7. Решить уравнение
Решение
Преобразуем уравнение:
Умножим левую часть уравнения на
Последнее уравнение - однородное четвертой степени относительно sinx и cosx.
Пусть
Задание 3
8 8. 90. 9 2. 9 4. 9 6. 9 7. 9 9. 101. 10 2. 10 3. 4. Для преобразования уравнений было использовано основное тригонометрическое тождество
отсюда находим
Далее,
Преобразуем сумму
Выше приведенные формулы очень часто используются при решении тригонометрических уравнений, и не только однородных.
Пример 10 5. Решите уравнение
Решение
Преобразуем уравнение, используя формулу (4): Пусть
Ответ: Пример 106. Решите уравнение
Решение Преобразуем уравнение, используя формулу (4):
Уравнение 2 - sin2x = 0, sin2x = 2 не имеет решений.
Ответ: Пример 107. Решите уравнение
Решение
Преобразуем уравнение, используя формулу:
Ответ:
Пример 108. Решите уравнение
Решение
Преобразуем уравнение, используя формулу:
Ответ:
Пример 10 9. Решите уравнение
Решение
Преобразуем уравнение, используя формулы:
получим:
Ответ:
Пример 1 10. Решите уравнение
Решение
Преобразуем уравнение, используя формулу (6)
Ответ:
Задание 4 111. 113. Метод замены переменных 4.1. Замена
Пусть дано некоторое тригонометрическое уравнение F(x) = 0. Обозначим через g(x) функцию Мы рассмотрим несколько случаев, когда это удается сделать. Введем (в некотором тригонометрическом уравнении) новое неизвестное
Ясно, что если уравнение содержит сумму функций
Если левая часть тригонометрического уравнения F(x) = 0 может быть выражена через
Пример 114. Решите уравнение
Решение
Пусть
Получим совокупность уравнений:
Ответ:
Замечание. Уравнение Аналогично решаются уравнения вида Здесь удобно положить Пример 115. Решите уравнение
Решение Й способ Положим
Ответ:
Й способ
| Поделиться:
| |
 и
и 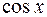 ....... 31
....... 31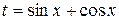 . 41
. 41 ............ 45
............ 45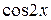 ........ 47
........ 47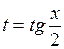 . Универсальная тригонометрическая подстановка 51
. Универсальная тригонометрическая подстановка 51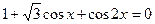 .
. .
.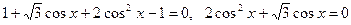 .
. .
.
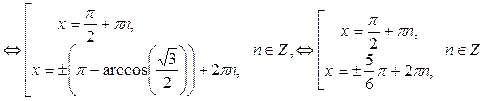 .
. .
.
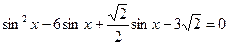


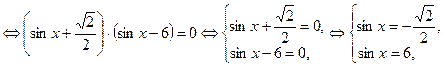
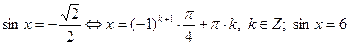 - решений не имеет.
- решений не имеет. .
.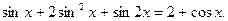
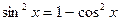 и
и  .
.
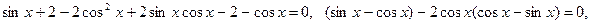
 .
. и (2)
и (2) 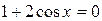 .
.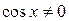 . В самом деле, если допустить противное, т. е., что
. В самом деле, если допустить противное, т. е., что  , тогда, подставив его в уравнение (1), найдем, что и
, тогда, подставив его в уравнение (1), найдем, что и  , что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество
, что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество  ). Итак,
). Итак, 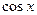 , получим
, получим 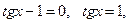
 .
.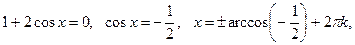
 .
. .
.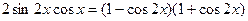 .
.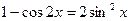 и
и  . Уравнение примет вид:
. Уравнение примет вид: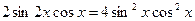 ,
,  ,
,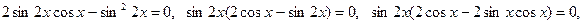
 .
.
 - это значит, что при четных значениях k из множества корней
- это значит, что при четных значениях k из множества корней  получаются корни
получаются корни 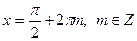 , значит,
, значит, 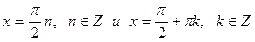 .
. , т. е. при нечетных значениях n из первого множества корней
, т. е. при нечетных значениях n из первого множества корней  получаются корни
получаются корни  , следовательно,
, следовательно, 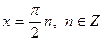 - являются общими решениями трех полученных результатов.
- являются общими решениями трех полученных результатов. .
.
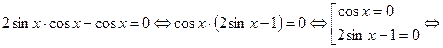
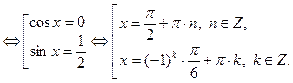
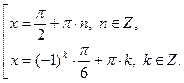

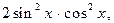 тогда уравнение примет вид
тогда уравнение примет вид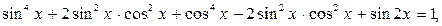
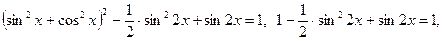

 - это уравнение не имеет решений, так как
- это уравнение не имеет решений, так как 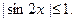
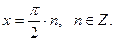
 .
. и
и 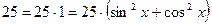 .
. , а затем все перенесем в левую часть и приведем подобные слагаемые:
, а затем все перенесем в левую часть и приведем подобные слагаемые:
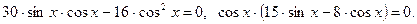
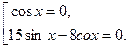
 .
.
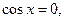 тогда подставив это значение в уравнение, получаем:
тогда подставив это значение в уравнение, получаем:  . Но одновременно
. Но одновременно 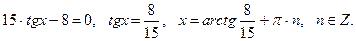
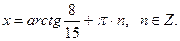
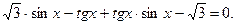
 .
.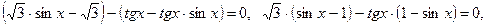
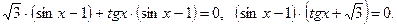

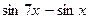 в произведение, получим
в произведение, получим
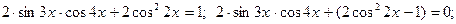
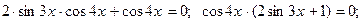
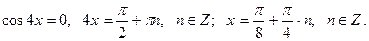
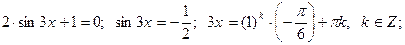

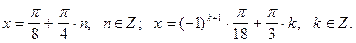



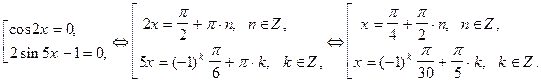
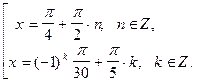
 .
. , получим:
, получим: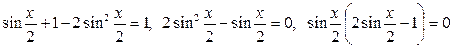 .
.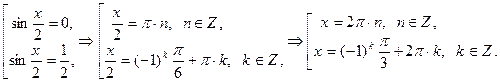




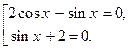
 решений не имеет, поскольку
решений не имеет, поскольку 
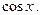
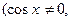 в противном случае, из уравнения, получим, что и
в противном случае, из уравнения, получим, что и 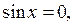 что невозможно). В результате деления на
что невозможно). В результате деления на  , приходим к уравнению:
, приходим к уравнению:

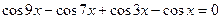 .
.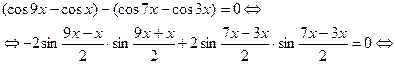

 .
.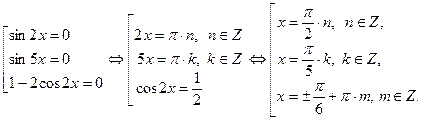
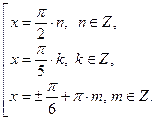
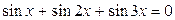 .
.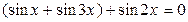 . Применим тождество преобразования суммы синусов в произведение:
. Применим тождество преобразования суммы синусов в произведение: 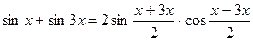 .
. .
.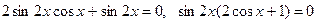 .
.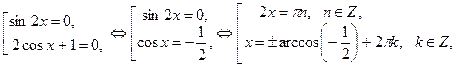
 .
. .
.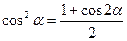 , получим:
, получим:
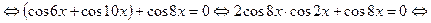
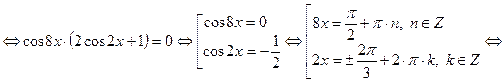


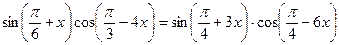 .
.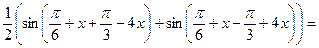

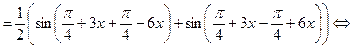


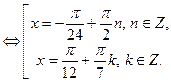

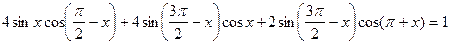 .
.

 .
.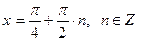 .
.
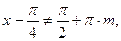
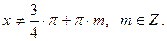
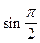 и преобразуя разность синусов, в правой части уравнения, в произведение. Тангенс, заменим на частное от деления синуса на косинус.
и преобразуя разность синусов, в правой части уравнения, в произведение. Тангенс, заменим на частное от деления синуса на косинус.
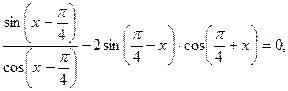
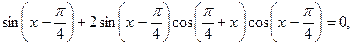
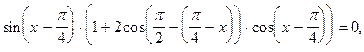

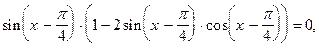



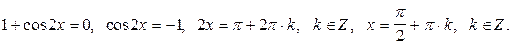
 . 28.
. 28. 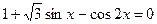 .
. .
. 31.
31.  .
. 33.
33.  .
. . 35.
. 35.  .
.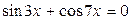 . 37.
. 37. 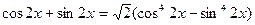 .
.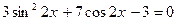 . 59.
. 59. 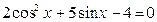 .
.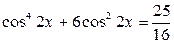 . 61.
. 61.  .
. . 63.
. 63. 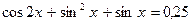 .
.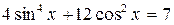 . 65.
. 65.  .
. . 67.
. 67.  .
. . 69.
. 69. 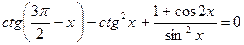 .
.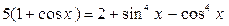 .
.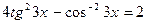 . 72.
. 72. 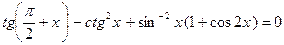 .
. . 74.
. 74.  .
.

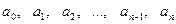 - действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно
- действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно  и
и 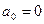 , то уравнение примет вид:
, то уравнение примет вид: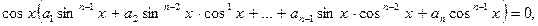 решениями которого являются значения x, при которых
решениями которого являются значения x, при которых  , т. е. числа
, т. е. числа 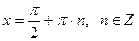 . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.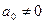 , то эти числа не являются корнями уравнения (1).
, то эти числа не являются корнями уравнения (1). получим:
получим: 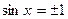 и левая часть уравнения (1) принимает значение
и левая часть уравнения (1) принимает значение 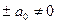 .
.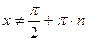 и
и 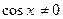 , поэтому можно разделить обе части уравнения на
, поэтому можно разделить обе части уравнения на  . В результате получаем уравнение:
. В результате получаем уравнение: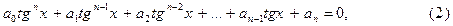
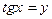 легко сводится к алгебраическому:
легко сводится к алгебраическому: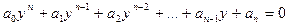 .
. имеем уравнение
имеем уравнение  .
. , то это уравнение равносильно уравнению
, то это уравнение равносильно уравнению  ,
, 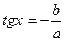 ,
, .
. .
.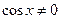 . Разделим обе его части на
. Разделим обе его части на 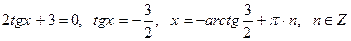 .
.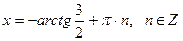 .
.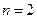 получим однородное уравнение вида
получим однородное уравнение вида .
. , получим уравнение
, получим уравнение 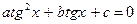 , которое подстановкой
, которое подстановкой  . Если
. Если  , то уравнение имеет действительные корни
, то уравнение имеет действительные корни  . Исходное уравнение будет иметь две группы решений:
. Исходное уравнение будет иметь две группы решений:  .
.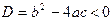 , то уравнение не имеет решений.
, то уравнение не имеет решений.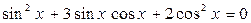 .
. . Пусть
. Пусть 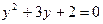 ,
,  ,
,  .
.  .
. .
.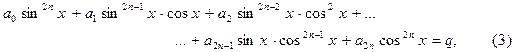
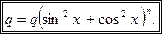
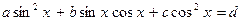 сводится к однородному, если заменить d на
сводится к однородному, если заменить d на 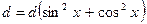 , тогда получим равносильное уравнение:
, тогда получим равносильное уравнение: 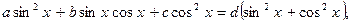
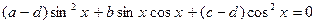 .
.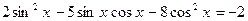 .
.
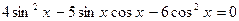 .
. , получим уравнение:
, получим уравнение: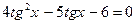 . Пусть
. Пусть  .
. .
.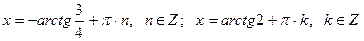 .
. .
. ,
,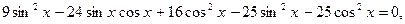
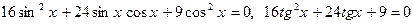 .
.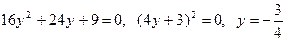 .
. .
.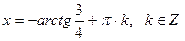 .
. .
. ,
,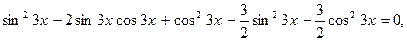
 .
. .
. ,
, ,
, .
. ,
,  . Умножим левую часть уравнения на
. Умножим левую часть уравнения на  , получим:
, получим:  .
. ,
,  .
. , получим:
, получим:  .
.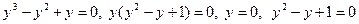 - не имеет корней.
- не имеет корней.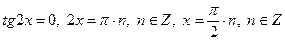 .
. .
. .
.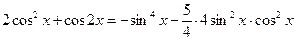 ,
, ,
, , получим:
, получим: ,
, ,
, ,
,  .
. , получим квадратное уравнение:
, получим квадратное уравнение:  ,
, .
.  - не удовлетворяет условию
- не удовлетворяет условию  и является посторонним корнем.
и является посторонним корнем.
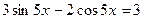 . 8 9.
. 8 9.  .
. . 9 1.
. 9 1.  .
. 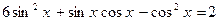 . 9 3.
. 9 3.  .
.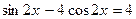 . 9 5.
. 9 5.  .
. .
. . 9 8.
. 9 8.  .
. . 100.
. 100.  .
. .
. .
. . 10 4.
. 10 4. 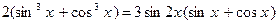 .
. . Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
. Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.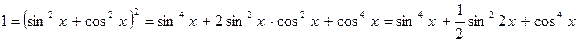 ,
, .
.
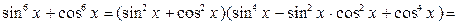
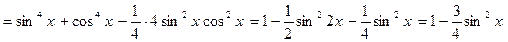 .
.
 , используя формулу (4).
, используя формулу (4).

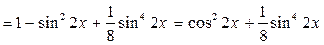 .
.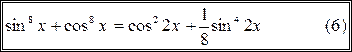
 .
.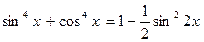 , получим уравнение:
, получим уравнение:  .
. приходим к квадратному уравнению:
приходим к квадратному уравнению: ,
,
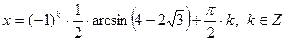 .
. .
.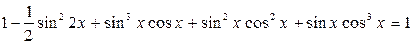 ,
,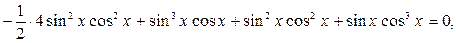
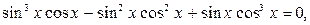
 ,
, .
. .
.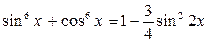 , получим:
, получим: 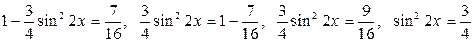

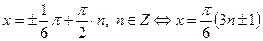 .
.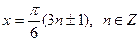 .
. .
.
 .
.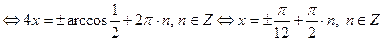
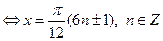 .
. .
.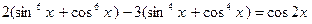 .
. и
и  ,
, ,
, .
.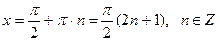 .
. .
.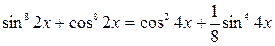 , получим уравнение:
, получим уравнение:
 . Пусть
. Пусть  , получим:
, получим:

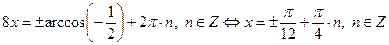 .
.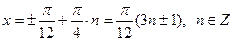 .
. . 112.
. 112.  .
. .
.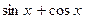 и введем новое неизвестное
и введем новое неизвестное  . Если удастся выразить функцию F(x) через t, т. е. представить ее в виде
. Если удастся выразить функцию F(x) через t, т. е. представить ее в виде  , то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через
, то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через  .
.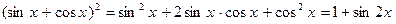 , находим
, находим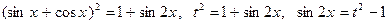 .
. , тогда его можно выразить через t.
, тогда его можно выразить через t. ,
,  .
. .
. .
. .
.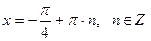 .
.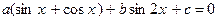 имеет решения в том и только в том случае, когда дискриминант уравнения
имеет решения в том и только в том случае, когда дискриминант уравнения 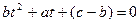 неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию
неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию  , так как
, так как  .
. .
. и тогда
и тогда 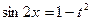 .
. .
.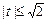 , получим уравнение:
, получим уравнение: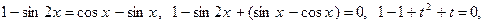
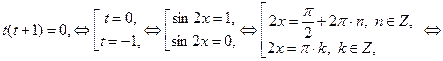


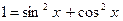 :
:


