
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Воздействие случайных процессов на линейные цепи ⇐ ПредыдущаяСтр 7 из 7
Задача статистического анализа линейных цепей или систем формулируется следующим образом:: на вход линейной системы с заданной импульсной характеристикой h(t) или комплексной частотной характеристикой K (ω) действует случайный процесс X(t) с заданной многомерной ПРВ Требуется найти многомерную той же размерности n или меньшей плотность ПРВ Это есть самый желательный вид решения данной задачи. Зная многомерную ПРВ случайного процесса y(t), можно найти все другие его статистические характеристики. Решение данной задачи в существенной мере зависит от того, являются ли начальные условия нулевыми или нет, рассматривается переходный режим работы линейной системы или установившийся (стационарный), является ли линейная система системой с детерминированными параметрами или случайными и т.д. Данная задача в сформулированном виде представляла собой в течение многих десятилетий одну из самых важных и сложных задач статистической радиотехники, радиофизики, теории связи и других областей науки. Для решения этой задачи были разработаны несколько методов, которые уместно назвать косвенными: метод моментов и моментных функций, метод квазимоментных функций, метод кумулятивных функций, метод дифференциальных уравнений, метод полигауссовых приближений, метод ортогональных разложений и метод статистических испытаний. Дело в том, что только в одном случае, а именно, когда на входе линейной системы действует гауссовский случайный процесс, эта задача решается совсем просто, т.к. случайный процесс на выходе линейной системы также будет гауссовским, а, следовательно, нужно найти лишь математическое ожидание и дисперсию процесса на выходе. Если случайный процесс на входе линейной системы не является гауссовским, то перечисленные методы позволяют найти в лучшем случае двумерную ПРВ случайного процесса y(t) на выходе линейной системы. Проблемы, возникающие при решении задачи статистического анализа линейных систем известными методами, рассмотрим на примере использования метода моментов и моментных функций. Пусть для случайного процесса x(t) на входе линейной системы задана многомерная ПРВ: Проблемы принципиального порядка возникают уже при отыскании одномерной ПРВ
Для неё справедлив интеграл Дюамеля:
Для отыскания ПРВ
Используя разложение характеристической функции
где Следовательно задача сводится к отысканию начальных моментов mk:
Для отыскания m3 понадобится p(x1,x2,x3;t1,t2,t3) и т.д. Так как ряд Маклорена функции Если ряд Маклорена для Непрерывную функцию с ограниченным изменением принято называть сингулярной, если её производная равна нулю почти всюду. Похожие трудности возникают при использовании других известных методов статистического анализа линейных систем. С точки зрения возможности этих методов, статистический анализ линейных систем в переходном режиме являются самым сложным. В последние годы разработан метод прямого статистического анализа линейных систем, который позволяет сравнительно просто решить рассматриваемую задачу для любых случайных (в том числе произвольных негауссовских) процессов, действующих на входе линейной системы. Рассмотрим наиболее простой случай. Пусть заданная импульсная характеристика h(t) описывает устойчивую одномерную линейную систему с постоянными параметрами произвольного порядка. Метод прямого статистического анализа линейных систем основывается на вводимом описании линейных систем в вероятностной области. При этом многомерная плотность распределения вероятностей мгновенных значений импульсной характеристики h(t) линейной системы с постоянными параметрами определяется выражением:
где hk – аргумент многомерной ПРВ в общем случае, hp(tk) – выборочное значение детерминированной регулярной функции или импульсной характеристики hp(t) линейной системы на интервале линейная система 1-го порядка линейная система 2-го порядка
Рис. 27 – Выборочные значения импульсных характеристик (справа – частный случай) Полагаем для определенности, что: 1) собственный шум линейной системы пренебрежимо мал; 2) случайные величины x1,x2,...,xn принимают действительные значения в интервале (-∞, +∞); 3) параметры линейной системы не зависят от случайного процесса X(t); 4) начальные условия нулевые; 5) рассматривается переходный процесс в работе линейной системы. При принятых условиях случайный процесс на выходе рассматриваемой линейной системы определяется интервалом Дюамеля:
С целью упрощения рассмотрим линейную систему 1-го порядка. Тогда случайный процесс x(t) на входе линейной системы и её импульсную характеристику можно изобразить так
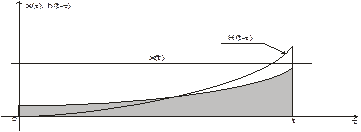
Рис. 28 – Случайный процесс и импульсная характеристика линейной цепи 1-го порядка При отыскании случайного процесса y(t) на выходе линейной системы можно воспользоваться следующим геометрическим представлением (рис.29)
Рис. 29 – Пояснение процесса формирования интеграла Дюамеля
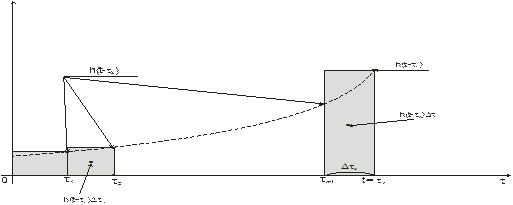
Пусть подынтегральная функция определяется пунктирной линией. Из рисунка видно, что y(t) определяется при этом заштрихованной площадью. Рис. 30 – Формирование множителей
Заменим интеграл Дюамеля «верхней» интегральной суммой:
\где Известно, что оценка Аналогично (2) множество величин
входящих в правую часть (4), имеет совместную ПРВ вида
Выполним следующее функциональное преобразование величины
Обратные функции однозначны:
Якобиан преобразования от величин
Тогда с учётом (6) – (9) совместная ПРВ величин
Здесь мы воспользовались следующим свойством дельта-функции:
Используя принятое условие о независимости параметров линейной системы от входного случайного процесса x(t), совместную ПРВ множеств {x1,…,xn} и {*h1*,…,*hn*} запишем в виде:
Выполним следующее функциональное преобразование величин *h1*,…,*hn*, входящих в (11), оставляя остальные случайные величины неизменными:
Обратные функции однозначны:
Якобиан преобразования от величин x1,…,xn, *h1*,…,*hn* к случайным величинам x1,…,xn, y1,…,yn
Тогда с учетом (10) – (14) совместная ПРВ случайных величин x1,…,xn, y1,…,yn принимает вид
Воспользовавшись условием согласованности многомерной ПРВ и интегрируя (15) по переменным x1,…,xn с использованием фильтрующего свойства дельта-функции, получим:
В соответствии с (4) выполним следующее функциональное преобразование случайных величин, входящих в (16):
Обратные функции однозначны:
Якобиан преобразования от случайных величин Тогда с учетом (16) – (18) совместная ПРВ случайных величин
Выражение (19) есть искомая многомерная произвольной размерности ПРВ случайного процесса y(t) на выходе линейной системы. Интегрируя (19) по “лишним” переменным, в соответствии с условием согласованности можно получить одномерную ПРВ соответствующую тому или иному моменту наблюдения tk. Например, для
Если входной случайный процесс X(t) является стационарным, а интервал наблюдения (0,t) равен Очень часто при решении задачи статистического анализа линейных систем ограничиваются заданием отдельных характеристик входного случайного процесса x(t), таких как спектральная плотность мощности Wx(ω), корреляционная функция R(τ) и т.д. В этом случае спектральная плотность мощности случайного процесса y(t) на выходе линейной системы определяется выражением:
Для корреляционной функции имеем:
Тогда Рассмотрим два предельных случая. 1. Эффективная ширина спектра Тогда в пределах полосы пропускания линейной системы можно положить, что Тогда
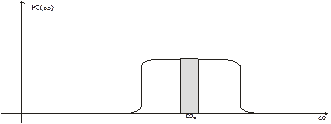
2. Эффективная ширина спектра
Рис.31 – Случай, когда эффективная ширина спектра шума много меньше полосы пропускания линейной цепи
Тогда Взаимная корреляционная функция случайных процессов на выходе и входе линейной цепи имеет вид
или
где h(.) – импульсная характеристика линейной системы. Взаимная корреляционная функция Rxy(τ) может быть получена так (через взаимный энергетический спектр):
Аналогично:
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.215 (0.044 с.) |
 .
.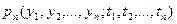 случайного процесса y(t) на выходе линейной системы.
случайного процесса y(t) на выходе линейной системы.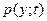 случайного процесса y(t) на выходе линейной системы с постоянными параметрами.
случайного процесса y(t) на выходе линейной системы с постоянными параметрами.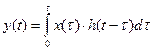 .
.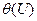 :
: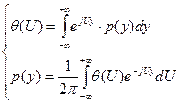 .
.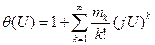 ,
,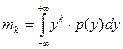 .
.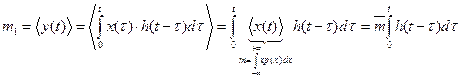

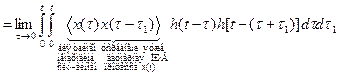 .
. . Выполнить это требование практически невозможно. Так появилась первая принципиальная трудность.
. Выполнить это требование практически невозможно. Так появилась первая принципиальная трудность.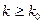 все
все  , то возникает вторая принципиальная трудность, состоящая в том, что не существует несингулярной функции, все высшие моменты которой равнялись бы нулю [3].
, то возникает вторая принципиальная трудность, состоящая в том, что не существует несингулярной функции, все высшие моменты которой равнялись бы нулю [3].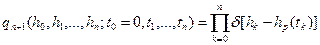 , (2)
, (2)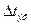 ,
, 
 . (3)
. (3)
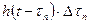 интегральной суммы
интегральной суммы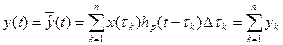 , (4)
, (4) ,
,  .
.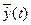 сходится в среднеквадратическом смысле к y(t) при n→∞ (при этом
сходится в среднеквадратическом смысле к y(t) при n→∞ (при этом 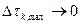 ).
).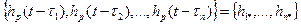 , (5)
, (5)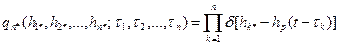 . (6)
. (6) , входящих в (5):
, входящих в (5):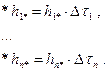 (7)
(7)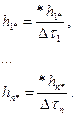 (8)
(8) к величинам
к величинам 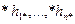 имеет вид
имеет вид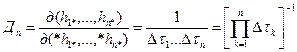 . (9)
. (9)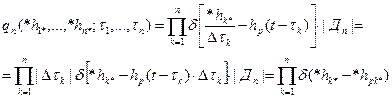 . (10)
. (10) .
.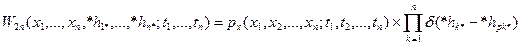 . (11)
. (11)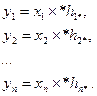 (12)
(12) (13)
(13) . (14)
. (14) . (15)
. (15) . (16)
. (16) (17)
(17) (18)
(18) к случайным величинам
к случайным величинам 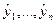 равны единице.
равны единице.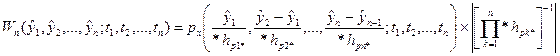 . (19)
. (19)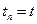 будем иметь
будем иметь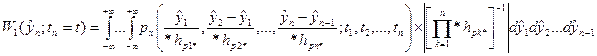 . (20)
. (20) , то выражение (20) можно также рассматривать как одномерную ПРВ случайного процесса y(t) на выходе линейной системы в установившимся режиме, т.е. после окончания переходного процесса. Таким образом, поставленная задача решена полностью.
, то выражение (20) можно также рассматривать как одномерную ПРВ случайного процесса y(t) на выходе линейной системы в установившимся режиме, т.е. после окончания переходного процесса. Таким образом, поставленная задача решена полностью.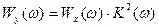 .
. .
.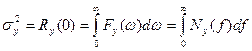 .
.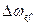 спектральной плотности Wx(ω) много больше полосы пропускания линейной системы.
спектральной плотности Wx(ω) много больше полосы пропускания линейной системы.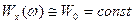 .
.

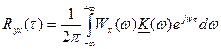 ,
,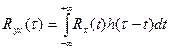 ,
,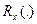 – корреляционная функция случайного процесса x(t),
– корреляционная функция случайного процесса x(t),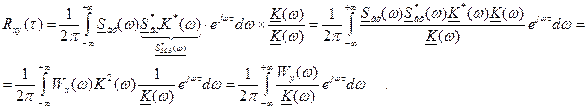
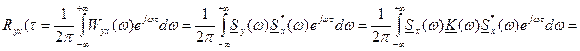
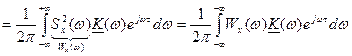 .
.


