
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели сообщений, сигналов и помехСтр 1 из 7Следующая ⇒
Лекция 1 Математические модели сообщений, сигналов и помех Сигналы и их спектральный анализ. Лекция 2 Лекция 3 Модулированные сигналы и их характеристики
Сигнал называется узкополосным, если отношение ширины спектра сигнала Δω к средней частоте спектра ωср удовлетворяет условию:
Если это условие нарушается, сигнал называется широкополосным или сверхширокополосным. С этой точки зрения все информационные сигналы S(t) являются сравнительно широкополосными и содержат низкие частоты. Пример: речевой сигнал (ширина полосы частот почти вдвое превышает центральную частоту). Для эффективной передачи по радиоканалам или для частотного уплотнения проводных (или кабельных) линий связи необходим перенос спектра информационного сигнала в область высоких частот так, чтобы выполнялось условие узкополосности:
Для этой цели в передатчике формируется специальный высокочастотный (ВЧ) сигнал, который называется несущим колебанием. Его математическая модель имеет вид
где а1,…,аn – параметры, определяющие форму этого колебания. Если хотя бы один из этих параметров изменяется пропорционально передаваемому сообщению S(t), то колебание Sнес(t) выступает уже в качестве переносчика информации. Физический процесс управления параметрами несущего колебания называется модуляцией. Наиболее частым и удобным переносчиком является гармоническое колебание. Но используются также и другие переносчики, в частности последовательность импульсов, шум и т.д. Модуляция – есть нелинейный (или параметрический) процесс, т.к. при модуляции в спектре несущего колебания появляются новые спектральные составляющие. Запишем несущее гармоническое колебание в виде
где Um, ω0 и φ0 соответственно амплитуда, несущая частота и начальная фаза колебания. Если пропорционально информационному сигналу S(t) изменяется амплитуда Um сигнала, такой сигнал называется сигналом с амплитудной модуляцией, а если – мгновенная частота ω, то имеет место сигнал с частотной модуляцией (ЧМ), ω= ω(t). Если пропорционально информационному сигналу S(t) изменяется полная фаза θ(t), такой сигнал называется сигналом с фазовой модуляцией или ФМ сигналом.
Существуют комбинированные виды модуляции разного рода. Всего видов модуляции очень много (особенно их много в цифровой связи). Пока мы рассмотрим самые простые.
Фазовая модуляция (ФМ)
При данном виде модуляции пропорционально сообщению S(t) изменяется полная фаза θ(t) несущего колебания:
где Если сообщение S(t) есть гармоническое колебание, т.е.
где При этом математическая модель сигнала с фазовой модуляцией имеет вид
Для мгновенной частоты этого сигнала имеем:
где Таким образом, при фазовой модуляции изменяется также мгновенная частота.
Частотная модуляция (ЧМ)
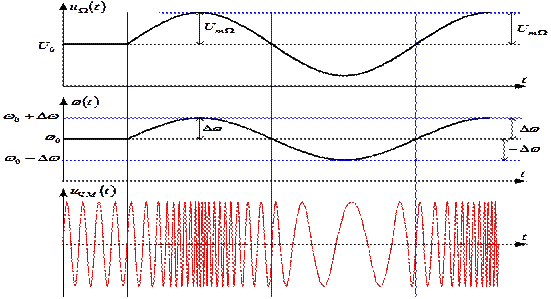
При данном виде модуляции пропорционально сообщению S(t) изменяется мгновенная частота:
Если
где Для полной фазы имеем
где
Математическая модель сигнала с частотной модуляцией имеет вид:
Различие сигналов с фазовой и частотной модуляциями проявляется только при модуляции сложным сообщением (смотри приведённые ниже рисунки).
Рис.17 – Качественное поведение параметров сигналов при фазовой и частотной модуляциях
Осциллограмма сигнала с ЧМ имеет вид
Рис.18 – Осциллограмма сигнала с ЧМ
Фазовая и частотная модуляции имеют общее название "угловая модуляция". Все основные свойства сигналов с угловой модуляцией достаточно четко видны при гармоническом сообщении. При этом оба вида модуляции неразличимы.
Спектры сигналов с угловой модуляцией
Полагаем
Следует иметь в виду 2 случая. 1. βУМ << 1. В этом случае справедливы соотношения: Тогда
В спектре – те же частоты, что и при АМ-колебании. Ширина спектра та же, что и у АМ-сигнала и равна
2. βУМ >> 1. При этом справедливы следующие разложения:
Тогда имеем следующее:
где Jn(o) – функция Бесселя порядка n. Ширина спектра:
Замечание: сигналы с угловой модуляцией получили достаточно широкое распространение, т.к. в условиях действия помех дают возможность передать сообщения по каналу связи с более высокой достоверностью, чем при АМ.
Лекция 4 Корреляционная функция
Для узкополосных случайных процессов функция корреляции из общего вида
может быть преобразована к виду
где F(.) – односторонняя спектральная плотность мощности случайного процесса,
Если спектр
где
Корреляционные свойства амплитуд A(t) и B(t)
Можно показать, что
При где Если Тогда совместную ПРВ огибающих A(t) и B(t) можно записать
Если случайный процесс x(t) – гауссовский, то A(t) и B(t) являются тоже гауссовскими, при этом mA=mB=0. Тогда совместная ПРВ определяется выражением
Найдем совместную ПРВ p(U,φ) (во второй записи узкополосного случайного процесса). Имеем:
Обратные функции однозначны (
Якобиан преобразования от случайных величин A и B к случайным величинам U и
Тогда
Отсюда по условию согласованности получим:
Таким образом, ПРВ фаза узкополосного случайного процесса равномерна в интервале [-π,π] или [0, 2π]:
Рис.26 – Два вида ПРВ фазы узкополосного случайного процесса
С другой стороны
Это ПРВ огибающей случайного процесса. Мы вывели распределение Релея. Если вместе с узкополосным шумом присутствует синусоидальный сигнал, а) по первой модели, по-прежнему: б) по второй модели: Рассмотрим функциональное преобразование:
Обратные функции однозначны:
Якобиан преобразования от A, B к U,
Тогда Отсюда можно получить одномерные ПРВ:
Это распределение Райса. При
т.е. при достаточно больших отношениях сигнал/шум ПРВ огибающей почти гауссовская.
Лекция 5 Лекция 1 Математические модели сообщений, сигналов и помех
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.232 (0.036 с.) |
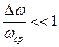 .
.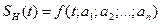 ,
,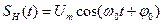 ,
,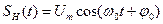 ,
, 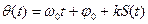 ,
,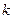 – коэффициент пропорциональности.
– коэффициент пропорциональности.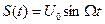 , то
, то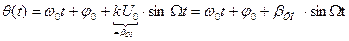 ,
,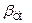 – коэффициент или индекс фазовой модуляции.
– коэффициент или индекс фазовой модуляции.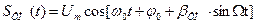 .
.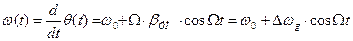 ,
,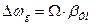 – девиация или максимальное отклонение мгновенной частоты сигнала от ω0.
– девиация или максимальное отклонение мгновенной частоты сигнала от ω0.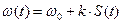 .
.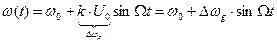 ,
,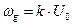 – девиация частоты.
– девиация частоты.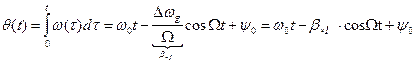 ,
,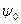 – постоянная интегрирования,
– постоянная интегрирования,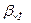 – коэффициент или индекс частотной модуляции.
– коэффициент или индекс частотной модуляции.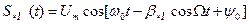 .
.
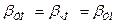 , φ0 и ψ0 с целью упрощения опускаем. Тогда:
, φ0 и ψ0 с целью упрощения опускаем. Тогда: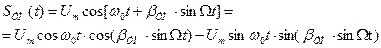 .
.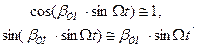
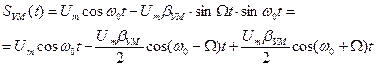 .
.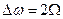 .
.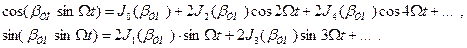
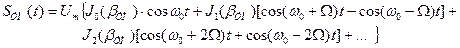 ,
,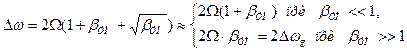 .
.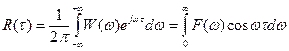
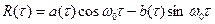 ,
,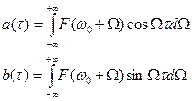 – медленные функции аргумента
– медленные функции аргумента 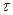 ,
,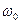 – центральная частота спектра узкополосного случайного сигнала.
– центральная частота спектра узкополосного случайного сигнала.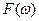 симметричен относительно
симметричен относительно  , тогда
, тогда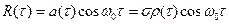 ,
,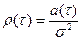 – огибающая корреляционной функции.
– огибающая корреляционной функции.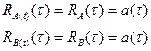 ,
,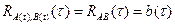 – взаимная корреляционная функция.
– взаимная корреляционная функция.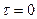 имеем, что
имеем, что 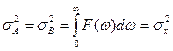 ,
,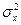 – дисперсия самого процесса x(t).
– дисперсия самого процесса x(t).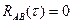 , откуда следует, что огибающие A(t) и B(t) в совпадающие моменты времени независимы.
, откуда следует, что огибающие A(t) и B(t) в совпадающие моменты времени независимы.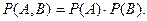
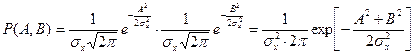 .
.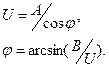
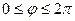 ):
):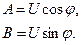
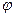 имеет вид
имеет вид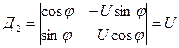 .
.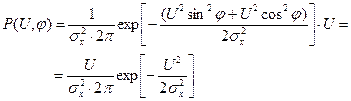 .
.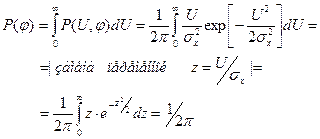 .
.

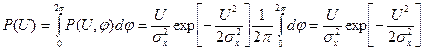 .
.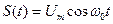 , то суммарный случайный процесс записывается так:
, то суммарный случайный процесс записывается так: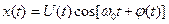 ,
,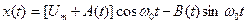 .
.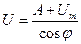 ,
,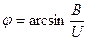 .
.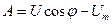 ,
,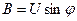 .
.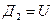 .
.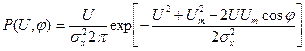 .
.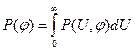 – распределение не является равномерным.
– распределение не является равномерным.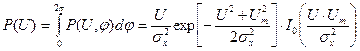 .
.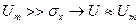 имеем приближенно
имеем приближенно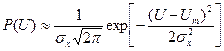 ,
,


