
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектральное представление сигналов
Спектры непериодических сигналов
Комплексный ряд Фурье сигнала S(t) преобразованного таким образом, запишем в виде
Устремим к ∞ период повторения Т. При этом следует отметить два момента: 1) Частоты соседних гармоник nΩ и (n+1)Ω станут как угодно близкими, что дает возможность дискретную частоту nΩ заменить на непрерывную переменную “ω”, т.е. nΩ→ ω. 2) Амплитуды коэффициентов С n станут неограниченно малыми (из-за Т в знаменателе). Таким образом при Т→∞ имеет место следующий переход: 1) 2) Тогда выражение для коэффициента С n преобразуются к виду
где функция Используя полученное предельное уравнение для коэффициента С n и понятие спектральной плотности сигнала
Таким образом, Пара преобразования Фурье представляют собой зависимость между временной и частотной областями.
Самостоятельно проработать все основные теоремы о спектрах. Их всего семь: 1. Спектральная плотность суммы сигналов. 2. Спектральная плотность сигнала, смещённого во времени. 3. Спектральная плотность производной сигнала. 4. Спектральная плотность интеграла от сигнала. 5. Спектральная плотность сигнала с изменённым масштабом времени. 6. Спектральная плотность произведения двух сигналов. 7. Смещение спектра сигнала (частный, но очень важный случай п.6, когда один из сигналов низкочастотный, а другой – высокочастотный).
Замечание. Если В остальных случаях:
Условие существования спектральной плотности сигнала Спектральная плотность определена выше только для абсолютно интегрируемых сигналов, т.е. сигналов, удовлетворяющих условию:
Такое условие существенно сужает класс сигналов, для которых существует
Математики нашли выход: предложили использовать понятие обобщенных функций и их теорию. К таким обобщенным функциям относится дельта-функция δ(ω). С её использованием можно говорить о спектральной плотности гармонического колебания. Например: Требуется найти спектр такого сигнала. В соответствии с общей формулой
Обобщенная формула Релея Рассмотрим понятие "скалярное произведение двух сигналов" в виде
Таким образом, нижнее выражение является наиболее общим. Из выражения Последнее выражение подставим в выражение для скалярного произведения двух комплексных сигналов:
Таким образом, имеем Это и есть обобщенная формула Релея. Она справедлива как для вещественных, так и для комплексных сигналов. При S1(t)=S2(t) имеем выражение для энергии сигнала
Величина
Справедливы следующие соотношения сигналов: В последнем выражении функции Относительная доля энергии сигнала S(t) содержится в некоторой полосе Δω, определяется по формуле:
Критерии бывают разные: 1) К=0,9 или К=90%, 2) К-0,95 или К=95%, 3) К=0,97 или К=97% и т.д. В зависимости от требуемой задачи выбирают тот или иной критерий и определяют требуемую полосу частот для сигнала.
Спектр прямоугольного видеоимпульса Математическая модель:
Спектральная плотность:
Спектр прямоугольного радиоимпульса Математическая модель:
Спектральная плотность:
Аналитический сигнал и преобразование Гильберта
Любой вещественный сигнал S(t) c известной спектральной плотностью
Функция
названа аналитическим сигналом, который соответствует вещественному сигналу S(t). Первый из интегралов при замене –ω=ξ преобразуется к виду
Удвоив это выражение, получим:
Из выведенных выражений следует, что
Можно показать, что Мнимая часть аналитического сигнала называется сигналом, сопряженным по Гильберту по отношению к исходному сигналу:
т.е. Спектральная плотность аналитического сигнала может быть определена по общей формуле:
Это видно из определения аналитического сигнала (умножить и разделить на 2):
Пусть Так как то в силу линейности преобразования Фурье имеем Но тогда с учетом (1) и (2) имеем:
и
Способ получения сигнала
Рис.5. Формирование сигнала, сопряжённого по Гильберту
Тогда Или
Обратное преобразование Гильберта имеет вид
т.е. они отличаются знаком. Символическая запись такова: Интегралы, входящие в преобразование Гильберта, следует понимать в смысле «главного значения»:
т.к. функция « Модуль аналитического сигнала, т.е. | Z S(t)|, определяет огибающую сигнала S(t):
Аргумент аналитического сигнала есть полная фаза колебания S(t):
Мгновенная частота сигнала S(t) есть производная от полной фазы:
Введение понятий аналитического сигнала и преобразований Гильберта дало возможность, в отличие то метода комплексных амплитуд, дать строгие определения понятий “огибающая” и “мгновенная частота” произвольного сигнала S(t).
Лекция 3
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.123.120 (0.03 с.) |
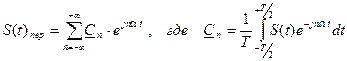 .
.
 .
.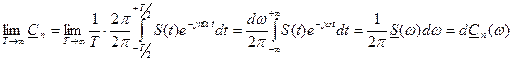 ,
, носит название спектральной плотности непериодического сигнала или прямое преобразование Фурье.
носит название спектральной плотности непериодического сигнала или прямое преобразование Фурье. , преобразуем комплексный ряд Фурье к виду
, преобразуем комплексный ряд Фурье к виду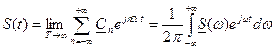 .
.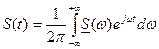 есть обратное преобразование Фурье.
есть обратное преобразование Фурье.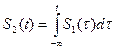 , то операция
, то операция  справедлива только для сигналов, у которых модуль спектральной плотности в нуле = 0, т.е. S1(0)=0 (модуль спектральной плотности). Это имеет место у сигналов с нулевой площадью:
справедлива только для сигналов, у которых модуль спектральной плотности в нуле = 0, т.е. S1(0)=0 (модуль спектральной плотности). Это имеет место у сигналов с нулевой площадью: 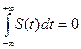 .
. .
. .
. . В этом смысле нельзя говорить о спектральной плотности гармонического сигнала S(t)=Umcosω0t, если на него не наложено условие ограниченности во времени.
. В этом смысле нельзя говорить о спектральной плотности гармонического сигнала S(t)=Umcosω0t, если на него не наложено условие ограниченности во времени. – постоянная составляющая.
– постоянная составляющая.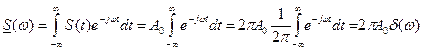 .
.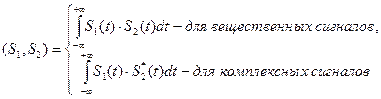 .
. следует
следует  .
.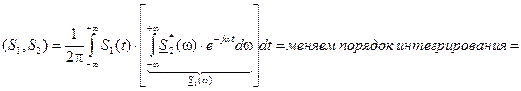
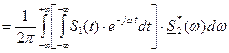 .
.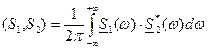 .
.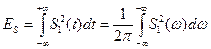 .
.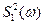 называется энергетическим спектром сигнала, а величина
называется энергетическим спектром сигнала, а величина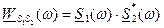 – взаимный энергетический спектр сигналов, поэтому
– взаимный энергетический спектр сигналов, поэтому .
.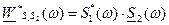 ,
, 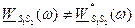 .
.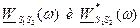 отличаются только знаком мнимой части, причём реальные части есть чётные функции, а мнимые части – нечётные, поэтому предыдущее выражение можно записать в виде
отличаются только знаком мнимой части, причём реальные части есть чётные функции, а мнимые части – нечётные, поэтому предыдущее выражение можно записать в виде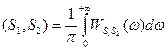 .
. .
.

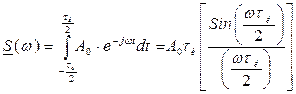 =
=  .
.  ,
,  .
. 

 .
.
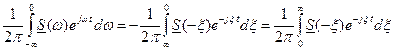 .
.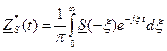 – сигнал, комплексно сопряженный аналитическому.
– сигнал, комплексно сопряженный аналитическому. .
. .
.
 , а
, а  .
. (1)
(1) .
. – спектральная плотность
– спектральная плотность  .
.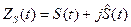 ,
, . (2)
. (2)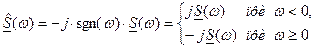
 .
.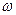 <0 и на угол φ= – 900 при
<0 и на угол φ= – 900 при 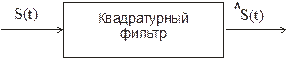
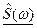 есть произведение
есть произведение  ”, следовательно, сигнал
”, следовательно, сигнал 
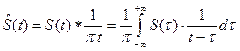 .
. – это и есть прямое преобразование Гильберта.
– это и есть прямое преобразование Гильберта. ,
,
 ,
, » имеет разрыв при t=τ.
» имеет разрыв при t=τ. .
.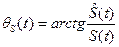 .
.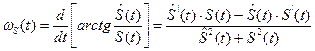 .
.


