
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратичные вычеты. Символ Лежандра⇐ ПредыдущаяСтр 13 из 13
Ранее мы рассматривали сравнения первой степени вида Поэтому далее будем изучать квадратичные сравнения вида (15.1). Определение 15.1. Пусть p нечетное простое число, Замечания. 1) Очевидно, что число 2) В определении 15.1 простое число p предполагалось нечетным, чтобы исключить тривиальный случай, когда При изучении квадратичных сравнений выделяют две задачи. 1) Задача распознавания: как узнать, является ли число a квадратичным вычетом по модулю p? 2) Задача поиска решений: как решить квадратичное сравнение? Мы рассмотрим только задачу распознавания как более легкую, но, при этом, имеющую практическое применение. Теорема 15.1. Пусть p – простое нечетное число. Тогда среди чисел из множества Доказательство. 1) Число Докажем, что квадраты чисел из любой пары сравнимы между собой по модулю p, аквадраты чисел из разных пар несравнимы по модулю p. Действительно, Докажем, что квадраты чисел из разных пар несравнимы по модулю p. Рассмотрим сравнение
2) Множество A состоит из всевозможных вычетов по модулю p (за исключением 0). Мы доказали, что каждой паре Пример. Пусть
При помощи теоремы 15.1 можно решать задачу распознавания, если числа a и p невелики. Рассмотрим способ решения этой задачи для случая произвольных значений a и p. Пусть p – простое нечетное число. Рассмотрим некоторые частные случаи для значений a. Рассмотрим сначала случай, когда Рассмотрим теперь случай, когда Если Если
Если число Если число Таким образом, мы получили, что число Рассмотрим случай, когда Определение 15.2. Рассмотрим квадратичное сравнение
если если Замечание. Если Символ Лежандра Исследуя случаи
Свойства символа Лежандра Свойство 1. Если Доказательство. 1) Пусть 2) Пусть 3) Пусть Свойство 2. Если Доказательство. Из условия следует, что Свойство 3 (Критерий Эйлера). Пусть p – простое нечетное число. Тогда Доказательство. 1) Пусть 2) Далее будем рассматривать случай, когда 3) Пусть a – квадратичный вычет по модулю p. Это означает, что найдется такое число 4) Пусть a – квадратичный невычет по модулю p. Тогда символ Лежандра Свойство 4 (мультипликативность символа Лежандра). Доказательство. Для доказательства утверждения воспользуемся критерием Эйлера: Свойство 5. В числителе символа Лежандра можно отбросить любой квадратичный множитель, не кратный p, то есть Доказательство. По критерию Эйлера Следующее свойство символа Лежандра примем без доказательства.
Свойство 6 (Квадратичный закон взаимности Гаусса). Для любых простых нечетных чисел p и q справедливо равенство На основании перечисленных свойств можно вычислять символы Лежандра Примеры. 1) Определить, имеет ли решение сравнение 2) Определить, имеет ли решение сравнение 3) Определить, имеет ли решение сравнение 4) Определить, имеет ли решение сравнение 5) Определить, имеет ли решение сравнение
Символ Якоби Полезным обобщением символа Лежандра является символ Якоби. Поскольку символ Якоби, обозначается так же, как и символ Лежандра, чтобы их различать иногда используют обозначения Определение 16.1. Пусть Замечание. Если число n – простое, то, очевидно, Символ Якоби можно вычислять, пользуясь его определением и свойствами символа Лежандра.
Пример. Найти
Символ Якоби обладает многими свойствами символа Лежандра, доказательство их справедливости следует из определения символа Якоби и свойств символа Лежандра. Свойство 1. Если Свойство 2. Если Свойство 3. (мультипликативность символа Якоби). Свойство 4. В числителе символа Якоби можно отбросить любой квадратичный множитель, не кратный n, то есть Свойство 5 (Квадратичный закон взаимности Гаусса). Для любых положительных нечетных взаимно простых чисел a и n справедливо равенство Для частных случаев, когда
Заметим, что критерий Эйлера для символа Якоби, вообще говоря, не выполняется.
Пример. Проверим верно ли сравнение С другой стороны, можно установить что
Использование символа Якоби.
1) Рассматривая символ Лежандра как частный случай символа Якоби и пользуясь свойствами последнего, можно упростить вычисление символа Лежандра. Пример. Имеет ли решение квадратичное сравнение Число 219 – составное,
Следовательно, квадратичное сравнение Если бы мы стали вычислять символ Лежандра 2) Символ Якоби можно также использовать для решения задачи распознавания для натурального нечетного модуля n, а именно для получения ответа на вопрос: имеет ли квадратичное сравнение Теорема 16.1. Рассмотрим квадратичное сравнение где n – нечетное натуральное число. Если символ Якоби Доказательство. Рассмотрим каноническое разложение числа n:
Если сравнение (16.1) имеет решение, то это означает, что найдется такое целое число x, для которого справедливо По определению символ Якоби равен произведению символов Лежандра:
Следовательно, символ Якоби Если же символ Якоби равен 1, то это может быть в случае, когда все символы Лежандра равны 1. Тогда найдется такое целое число x, что Но символ Якоби может быть равен 1 также в случае, когда среди составляющих его символов Лежандра имеются равные Пример. Выше было установлено, что
Проверка чисел на простоту Простые числа играют исключительно важную роль в жизни людей. На основе свойств простых чисел создаются различные способы шифрования, которые обеспечивают безопасность банковских операций, электронной почты, мобильной телефонной связи и многого другого. Поэтому задача поиска простых чисел чрезвычайно важна, однако пока еще никому не удалось найти формулу или алгоритм, позволяющий генерировать простые числа. Чтобы объявить найденное тем или иным способом число простым, требуется доказать его простоту. Существует большое количество способов проверки чисел на простоту. Среди них есть детерминированные, то есть дающие определенный ответ на вопрос, является ли число простым или нет. Есть также вероятностные способы проверки чисел на простоту, то есть объявляющие число простым только с некоторой вероятностью. Напомним определение простого числа (см. определение 8.1). Натуральное число называется простым, если оно имеет ровно два различных делителя. Если натуральное число имеет больше двух различных делителей, то оно называется составным. Одним из детерминированных способов проверки чисел на простоту является решето Эратосфена. Этот способ состоит в следующем. Мы хотим составить ряд простых чисел, не превосходящих натуральное число n. Для этого выпишем числа 1, 2, …, n. (17.1) Первое большее 1 число из этого ряда есть 2. Оно имеет ровно два различных делителя – числа 1 и 2, следовательно, оно является простым. Далее вычеркнем из ряда (17.1) все числа, кратные 2, кроме самого числа 2, так как они являются составными. Первым, следующим за числом 2, невычеркнутым числом является 3. Оно не делится на 2 (иначе оно оказалось бы вычеркнутым). Следовательно число 3 является простым. Вычеркнем из оставшихся чисел ряда (17.1) все числа, кратные 3, кроме самого числа 3. Первым, следующим за числом 3, невычеркнутым числом является 5, которое также является простым. Продолжая этот процесс и отбросив число 1, получим, что “высеянными” из ряда (17.1) числами оказались простые числа. Заметим, что составление ряда простых чисел, не превосходящих n, заканчивается после вычеркивания всех чисел, кратных простым, не превосходящим Этот древний способ (III-II в. до н. э.) дожил до наших дней, претерпев немало превращений и послужив основой для получения важных результатов теории чисел. Пример. Найдем простые числа из ряда 1, 2, …, 100. Для этого составим список всех натуральных чисел от 1 до 100. Затем вычеркнем из списка все числа, кратные числу 2, кроме самого числа 2: 4, 6,8,…. Затем из оставшихся чисел вычеркнем все числа, кратные 3, кроме самого числа 3: 9, 15, 21,…. Затем проделаем то же самое для чисел, кратных 5 и 7. После этого процесс будет окончен, поскольку следующее первое число из невычеркнутых будет число 11, превосходящее 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 – это все простые числа из первой сотни.
Рассмотрим теперь один из вероятностных способов проверки числа на простоту. Вероятностный тест Соловея-Штрассена Тест Соловея-Штрассена основан на том факте, что символ Якоби Введем следующее определение. Определение 17.1. Пусть то число a называется Эйлеровым свидетелем простоты числа n. Определение 17.2. Составные числа n, удовлетворяющие критерию Эйлера называются псевдопростыми числами Эйлера-Якоби. Рассмотрим натуральное число n. Проверка числа n на простоту методом Соловея-Штрассена опирается на следующую теорему, которую примем без доказательства. Теорема 17.1. Если n – нечетное составное число, то количество целых чисел a, взаимно простых с n, не превосходящих n и при этом удовлетворяющих критерию Эйлера (т. е. количество Эйлеровых свидетелей простоты числа n, не превосходящих n), не превосходит Алгоритм теста Соловея-Штрассена Алгоритм параметризуется количеством раундов k. В каждом раунде случайным образом выбирается число a: Если (17.2) не выполняется, то выносится решение, что число n составное. Если же (17.2) выполняется, то число n может быть как простым, так и составным. В этом случае число a является Эйлеровым свидетелем простоты числа n. По теореме 17.2 свидетелей простоты числа n не более, чем Поскольку число n, как правило, достаточно велико, можно считать, что случайные события, состоящие в выборе числа a в каждом раунде, являются независимыми. Поэтому если в k раундах, выбранные числа a оказались Эйлеровыми свидетелями простоты, то вероятность того, что число n – составное, не превосходит Пример. Пусть Раунд 1. Положим Раунд 2. Положим
и Раунд 3. Положим
и
Теория чисел в криптографии
Рассмотрим пример использования результатов теории чисел в криптографии. В 1977 году трое ученых Рональд Ривест, Ади Шамир и Леонард Адельман из Массачусетского технологического института (MIT) опубликовали алгоритм, названный RSA. Алгоритм основан на том, что некоторые вычислительные операции совершить относительно просто, а обратные – сложно.
Описание алгоритма. Предположим, что два человека А (Алиса) и B (Боб) договорились об использовании алгоритма RSA. Предположим, что B хочет отправить А секретное сообщение. Под сообщением будем понимать число. Действительно, любой текст, состоящий из слов, можно представить в виде упорядоченного набора цифр. Например, букве А можно поставить в соответствие цифру 1, букве Б – цифру 2 и т. д. Буквы в слове можно отделять друг от друга цифрой 0. Действия A и B состоят в следующем. 1) А выбирает два простых числа p и q и вычисляет их произведение 2) А вычисляет значение функции Эйлера от числа n: 3) А выбирает чи
|
|||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 1656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.111.9 (0.136 с.) |
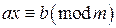 . Были установлены условия, при которых эти сравнения имеют решения, и найдены способы нахождения этих решений. Теперь рассмотрим квадратичные сравнения, то есть сравнения вида
. Были установлены условия, при которых эти сравнения имеют решения, и найдены способы нахождения этих решений. Теперь рассмотрим квадратичные сравнения, то есть сравнения вида 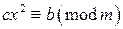 . Заметим, что сравнение такого вида можно упростить. Для этого положим
. Заметим, что сравнение такого вида можно упростить. Для этого положим 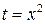 и решим сравнение первой степени
и решим сравнение первой степени 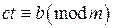 относительно
относительно 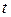 . Получим сравнение вида
. Получим сравнение вида 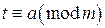 , или, что то же самое,
, или, что то же самое,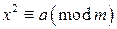 (15.1)
(15.1)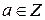 . Число a называется квадратичным вычетом по модулю p, если сравнение
. Число a называется квадратичным вычетом по модулю p, если сравнение 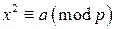 имеет решение. Если это сравнение решений не имеет, то число a называется квадратичным невычетом по модулю p.
имеет решение. Если это сравнение решений не имеет, то число a называется квадратичным невычетом по модулю p.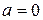 является квадратичным вычетом по модулю p для любого числа p. Поэтому в дальнейшем число
является квадратичным вычетом по модулю p для любого числа p. Поэтому в дальнейшем число 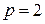 . Действительно, сравнение
. Действительно, сравнение 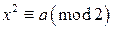 всегда имеет решение. Легко проверить, что в случае, когда число a четное, любое четное число x является решением данного сравнения, а в случае, когда число a нечетное, любое нечетное число x является решением данного сравнения.
всегда имеет решение. Легко проверить, что в случае, когда число a четное, любое четное число x является решением данного сравнения, а в случае, когда число a нечетное, любое нечетное число x является решением данного сравнения.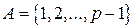 ровно половина является квадратичными вычетами по модулю p.
ровно половина является квадратичными вычетами по модулю p.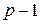 – четное, значит,
– четное, значит, 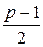 – целое. Разобьем множество A на пары чисел вида
– целое. Разобьем множество A на пары чисел вида 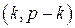 ,
, 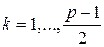 .
.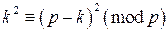
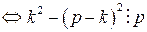
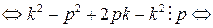
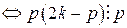 , что, очевидно, верно.
, что, очевидно, верно.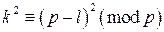 , при очевидном условии, что
, при очевидном условии, что 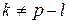 . Предположим, что оно выполняется для некоторого k, где
. Предположим, что оно выполняется для некоторого k, где 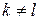 . Тогда
. Тогда 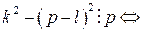
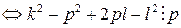
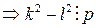 . Поскольку число p простое, справедливо
. Поскольку число p простое, справедливо 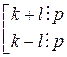 . Но
. Но 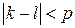 , значит
, значит 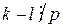 . Тогда выполняется
. Тогда выполняется 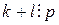 . При этом
. При этом 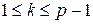 и
и 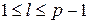 , следовательно,
, следовательно, 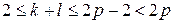 . Тогда утверждение
. Тогда утверждение 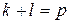 , или
, или 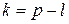 , что невозможно. Следовательно, сделанное предположение о сравнимости по модулю p квадратов двух чисел из разных пар, неверно.
, что невозможно. Следовательно, сделанное предположение о сравнимости по модулю p квадратов двух чисел из разных пар, неверно.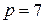 . Рассмотрим множество
. Рассмотрим множество 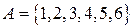 и пары чисел из A вида
и пары чисел из A вида 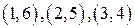 . Тогда справедливы сравнения:
. Тогда справедливы сравнения: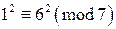 ,
, 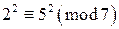 ,
, 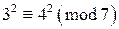 . При этом
. При этом 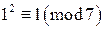 ,
, 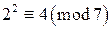 ,
, 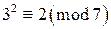 . Таким образом, числа 1, 2 и 4 являются квадратичными вычетами по модулю 7, а числа 3, 5 и 6 – квадратичными невычетами по модулю 7.
. Таким образом, числа 1, 2 и 4 являются квадратичными вычетами по модулю 7, а числа 3, 5 и 6 – квадратичными невычетами по модулю 7.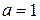 . Очевидно, что для любого p число 1 является квадратичным вычетом по модулю p. Действительно, сравнение
. Очевидно, что для любого p число 1 является квадратичным вычетом по модулю p. Действительно, сравнение 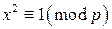 имеет решения
имеет решения 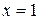 и
и 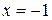 .
.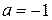 и выясним, в каких случаях сравнение
и выясним, в каких случаях сравнение 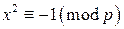 имеет решение.
имеет решение.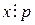 , то
, то 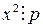 . Тогда
. Тогда 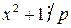 , а, значит, сравнение
, а, значит, сравнение 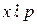 , то
, то 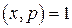 . Значит, выполняются условия теоремы Ферма, тогда
. Значит, выполняются условия теоремы Ферма, тогда 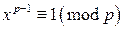 . Пусть x – решение сравнения
. Пусть x – решение сравнения 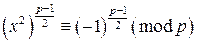
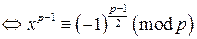 .
.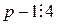 ), то
), то 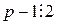 , но
, но 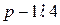 ), то
), то 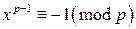 . Но по теореме Ферма
. Но по теореме Ферма 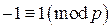
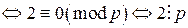 , что неверно в силу того, что
, что неверно в силу того, что 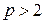 .
.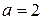 . Примем без доказательства факт, что сравнение
. Примем без доказательства факт, что сравнение 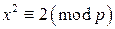 имеет решение в случае, когда число
имеет решение в случае, когда число 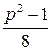 четное (т. е.
четное (т. е. 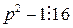 ), и не имеет решений в противном случае.
), и не имеет решений в противном случае. , определяемая следующим образом:
, определяемая следующим образом: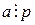 , то
, то 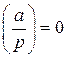 ;
;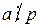 , то
, то 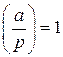 , в случае, когда a является квадратичным вычетом по модулю p и
, в случае, когда a является квадратичным вычетом по модулю p и 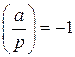 , в случае, когда a является квадратичным невычетом по модулю p.
, в случае, когда a является квадратичным невычетом по модулю p.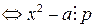 . Это утверждение выполняется для любого значения x, кратного числу p. Следовательно, в случае, когда
. Это утверждение выполняется для любого значения x, кратного числу p. Следовательно, в случае, когда 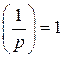 ,
, 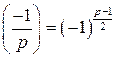 ,
, 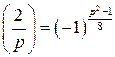 .
.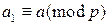 , то
, то 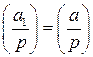 .
.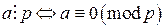 . Но
. Но 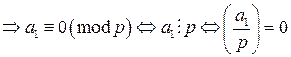 .
.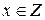 , что
, что 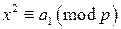 , следовательно,
, следовательно, 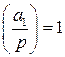 .
.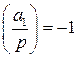 . Предположим, что это утверждение неверно. Тогда либо
. Предположим, что это утверждение неверно. Тогда либо 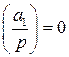 и, как следует из пункта 1) доказательства,
и, как следует из пункта 1) доказательства, 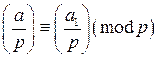 , то
, то 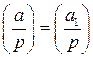 .
.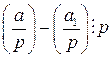 . Поскольку символ Лежандра принимает значения равные только 0, 1 или
. Поскольку символ Лежандра принимает значения равные только 0, 1 или 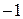 , разность
, разность 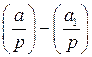 может принимать значения равные
может принимать значения равные 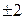 ,
, 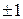 или 0, а из этих чисел только 0 делится на p. Значит,
или 0, а из этих чисел только 0 делится на p. Значит, 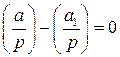 .
.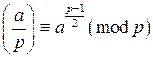 .
.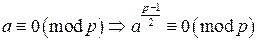 . По определению символа Лежандра
. По определению символа Лежандра 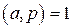 . Тогда по теореме Ферма
. Тогда по теореме Ферма 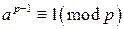
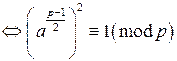
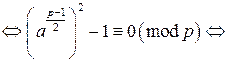
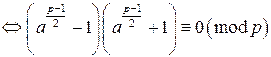
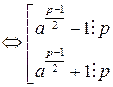 . При этом выполняется ровно одно из двух последних утверждений. Действительно, если бы выполнялись оба, то разность
. При этом выполняется ровно одно из двух последних утверждений. Действительно, если бы выполнялись оба, то разность 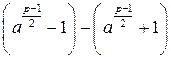 также делилась бы на p, а поскольку эта разность равна
также делилась бы на p, а поскольку эта разность равна 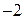 , то на p она не делится.
, то на p она не делится.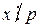 , поскольку если бы
, поскольку если бы 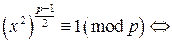
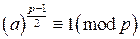 . Но поскольку a – квадратичный вычет по модулю p, символ Лежандра
. Но поскольку a – квадратичный вычет по модулю p, символ Лежандра 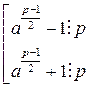 . Если бы выполнялось первое условие, то по доказанному в пункте 3), число a было бы квадратичным вычетом по модулю p, что неверно. Следовательно, выполняется второе условие, а это значит, что и в данном случае
. Если бы выполнялось первое условие, то по доказанному в пункте 3), число a было бы квадратичным вычетом по модулю p, что неверно. Следовательно, выполняется второе условие, а это значит, что и в данном случае 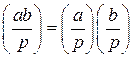 .
. 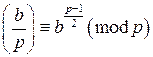 и
и 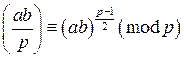 . Cвойство 5 сравнений утверждает, что сравнения по одному модулю можно почленно перемножать, значит
. Cвойство 5 сравнений утверждает, что сравнения по одному модулю можно почленно перемножать, значит 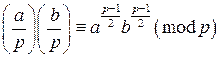 , откуда и следует требуемое равенство.
, откуда и следует требуемое равенство.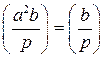 при
при 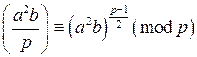
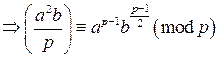 . Также по критерию Эйлера имеем
. Также по критерию Эйлера имеем 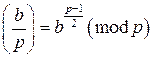 . По теореме Ферма
. По теореме Ферма 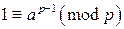 . Перемножая правые и левые части двух последних сравнений, получим
. Перемножая правые и левые части двух последних сравнений, получим 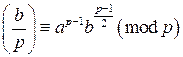 . Тогда
. Тогда 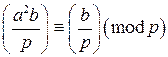 . По свойству 2 символа Лежандра получим требуемое утверждение.
. По свойству 2 символа Лежандра получим требуемое утверждение.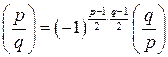 .
.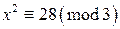 . Вычислим символ Лежандра
. Вычислим символ Лежандра 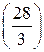 . Поскольку
. Поскольку 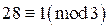 , по свойству 1 символа Лежандра имеем:
, по свойству 1 символа Лежандра имеем: 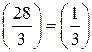 , а, как было установлено выше,
, а, как было установлено выше, 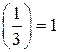 , следовательно, данное квадратичное сравнение имеет решение.
, следовательно, данное квадратичное сравнение имеет решение.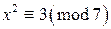 . Вычислим символ Лежандра
. Вычислим символ Лежандра 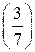 . По критерию Эйлера
. По критерию Эйлера 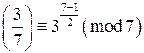 . Следовательно,
. Следовательно, 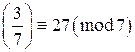 , но
, но 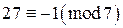 , значит
, значит 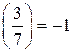 , и сравнение решений не имеет.
, и сравнение решений не имеет.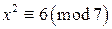 . Вычислим символ Лежандра
. Вычислим символ Лежандра 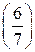 . По мультипликативному свойству символа Лежандра
. По мультипликативному свойству символа Лежандра 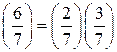 . Поскольку
. Поскольку 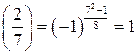 , а, как было установлено в примере 2,
, а, как было установлено в примере 2, 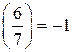 . Значит, данное квадратичное сравнение решений не имеет.
. Значит, данное квадратичное сравнение решений не имеет.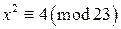 . Вычислим символ Лежандра
. Вычислим символ Лежандра 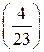 . По свойству 5 символа Лежандра
. По свойству 5 символа Лежандра 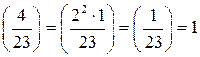 . Следовательно, данное сравнение имеет решение.
. Следовательно, данное сравнение имеет решение.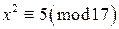 ? Вычислим символ Лежандра
? Вычислим символ Лежандра 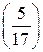 . По квадратичному закону взаимности Гаусса
. По квадратичному закону взаимности Гаусса 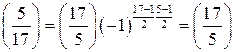 . Воспользуемся свойством 1 символа Лежандра, получим
. Воспользуемся свойством 1 символа Лежандра, получим 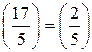 , и, как было отмечено выше,
, и, как было отмечено выше, 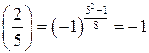 . Значит, данное квадратичное сравнение решений не имеет.
. Значит, данное квадратичное сравнение решений не имеет.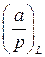 для символа Лежандра и
для символа Лежандра и 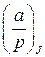 для символа Якоби.
для символа Якоби.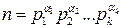 , где
, где 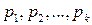 – простые числа, а
– простые числа, а 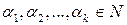 . Символом Якоби называется величина, обозначаемая
. Символом Якоби называется величина, обозначаемая 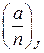 , определяемая следующим образом:
, определяемая следующим образом: 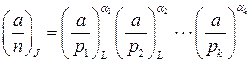 .
.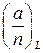
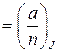 . В дальнейшем иногда при записи символа будем опускать индексы
. В дальнейшем иногда при записи символа будем опускать индексы  и
и 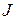 , если из контекста понятно, о каком символе идет речь. А именно, если в знаменателе символа стоит составное число, то имеется в виду символ Якоби, если же в знаменателе символа стоит простое число, то имеется в виду символ Лежандра, который в данном случае совпадает с символом Якоби.
, если из контекста понятно, о каком символе идет речь. А именно, если в знаменателе символа стоит составное число, то имеется в виду символ Якоби, если же в знаменателе символа стоит простое число, то имеется в виду символ Лежандра, который в данном случае совпадает с символом Якоби.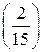 . Заметим, что
. Заметим, что 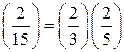 . В правой части последнего равенства стоит произведение символов Лежандра, поскольку знаменатели символов – простые числа. Тогда
. В правой части последнего равенства стоит произведение символов Лежандра, поскольку знаменатели символов – простые числа. Тогда 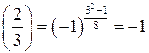 ,
, 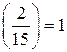 .
.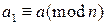 , то
, то 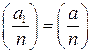 .
.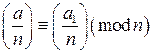 , то
, то 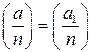 .
.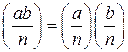 .
. 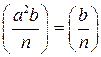 при
при 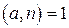 .
.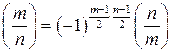 .
.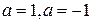 и
и 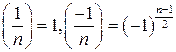 и
и 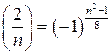 .
.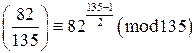 . Заметим, что в левой части сравнения стоит символ Якоби, так как в знаменателе символа стоит составное число 135. Рассмотрим каноническое разложение числа в знаменателе символа Якоби:
. Заметим, что в левой части сравнения стоит символ Якоби, так как в знаменателе символа стоит составное число 135. Рассмотрим каноническое разложение числа в знаменателе символа Якоби: 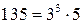 . Вычислим по определению символа Якоби
. Вычислим по определению символа Якоби 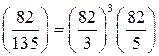 . В правой части этого равенства стоит произведение символов Лежандра. Тогда, по свойствам символа Лежандра получим
. В правой части этого равенства стоит произведение символов Лежандра. Тогда, по свойствам символа Лежандра получим 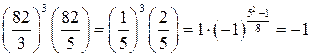 , следовательно,
, следовательно, 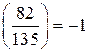 .
.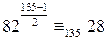 . Следовательно, данное сравнение не верно, что означает, что критерий Эйлера для символа Якоби, вообще говоря, не выполняется.
. Следовательно, данное сравнение не верно, что означает, что критерий Эйлера для символа Якоби, вообще говоря, не выполняется.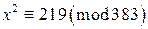 ?
?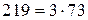 , а число 383 – простое, поэтому
, а число 383 – простое, поэтому 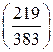 – символ Лежандра, и при этом
– символ Лежандра, и при этом 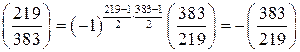 . По свойствам символа Якоби:
. По свойствам символа Якоби: 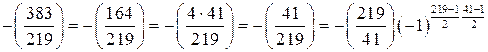
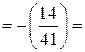
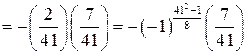
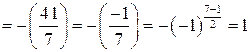 .
.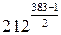 на 383, что было бы более трудоемко, чем способ, который мы использовали.
на 383, что было бы более трудоемко, чем способ, который мы использовали.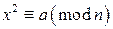 решение? Ответ на этот вопрос дает следующая теорема.
решение? Ответ на этот вопрос дает следующая теорема.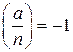 , то сравнение (16.1) не имеет решений, если же символ Якоби
, то сравнение (16.1) не имеет решений, если же символ Якоби 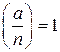 , то сравнение (16.1) может иметь решения, а может и не иметь решений.
, то сравнение (16.1) может иметь решения, а может и не иметь решений.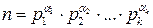 , где числа
, где числа 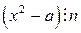 . Тогда
. Тогда 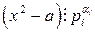 , для всех
, для всех 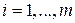 . Если же сравнение (16.1) не имеет решений, то для любого целого числа x выполняется
. Если же сравнение (16.1) не имеет решений, то для любого целого числа x выполняется 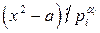 для некоторого i.
для некоторого i.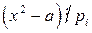 для некоторого i. Следовательно,
для некоторого i. Следовательно, 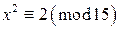 имеет решение. Действительно, если бы данное сравнение имело решение, то для некоторого значения x выполнялось бы
имеет решение. Действительно, если бы данное сравнение имело решение, то для некоторого значения x выполнялось бы 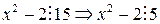 . Если число делится на 5, то его последняя цифра – либо 0, либо 5. Но тогда число
. Если число делится на 5, то его последняя цифра – либо 0, либо 5. Но тогда число 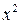 оканчивается либо на 2, либо на 7, а такого быть не может, так как квадраты целых чисел ни на 2, ни на 7 не оканчиваются.
оканчивается либо на 2, либо на 7, а такого быть не может, так как квадраты целых чисел ни на 2, ни на 7 не оканчиваются.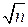 (см. следствие к теореме 8.3).
(см. следствие к теореме 8.3).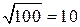 . Вычеркнем также число 1. В результате получим числа:
. Вычеркнем также число 1. В результате получим числа: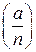 , вообще говоря, не удовлетворяет критерию Эйлера для составных чисел n.
, вообще говоря, не удовлетворяет критерию Эйлера для составных чисел n.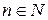 ,
, 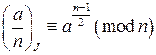 ,
,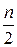 .
.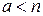 . Если оказывается, что
. Если оказывается, что 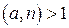 , то, очевидно, число n – составное. В противном случае проверяется справедливость сравнения
, то, очевидно, число n – составное. В противном случае проверяется справедливость сравнения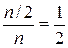 .
.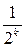 . Тогда число n оказывается простым с вероятностью не менее, чем
. Тогда число n оказывается простым с вероятностью не менее, чем 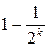 .
.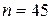 . Проверим число n на простоту при помощи теста Соловея-Штрассена.
. Проверим число n на простоту при помощи теста Соловея-Штрассена.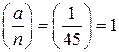 и
и 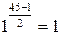 . Следовательно, (17.2) выполняется, значит число n – простое с вероятностью не менее, чем
. Следовательно, (17.2) выполняется, значит число n – простое с вероятностью не менее, чем 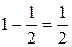 .
. . Тогда
. Тогда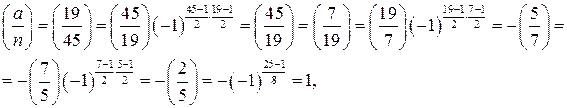
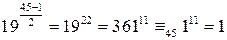 . Следовательно, (17.2) выполняется, значит число n – простое с вероятностью не менее, чем
. Следовательно, (17.2) выполняется, значит число n – простое с вероятностью не менее, чем 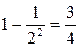 .
.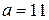 . Тогда
. Тогда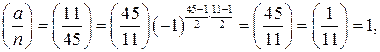
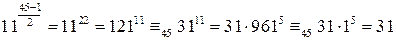 . Следовательно, (17.2) не выполняется, значит число 45 является составным.
. Следовательно, (17.2) не выполняется, значит число 45 является составным.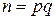 .
.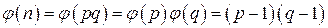 .
.


