
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы сравнений. Китайская теорема об остатках
Ранее мы рассматривали различные способы решения сравнений первой степени. Теперь рассмотрим вопрос о решении систем сравнений. Мы сформулируем условия достаточные для существования решения системы сравнений и построим алгоритм нахождения решения для случая, когда модули сравнений системы попарно взаимно просты. Рассмотрим систему сравнений: где числа Требуется найти число x, удовлетворяющее системе сравнений (11.1). Для решения поставленной задачи докажем теорему: Теорема 11.1. Пусть числа Сформулированная теорема носит название китайской теоремы об остатках, поскольку была доказана в Китае в 1-м (а по другим сведениям в 4-м веке) н. э.. Известны несколько доказательств этой теоремы. Мы рассмотрим конструктивное доказательство, т. е. доказательство существования решения путем построения решения. Для доказательства теоремы докажем вспомогательное утверждение. Лемма. Пусть числа
Доказательство. Положим Таким образом, для существования искомого числа Доказательство теоремы. Возьмем в качестве x какое-либо число, удовлетворяющее условию
Из определения x следует, что,
Выпишем теперь последовательность действий, которые требуется совершить, чтобы найти решение системы сравнений. Алгоритм решения системы сравнений вида (11.1) 1. Вычислить 2. Найти числа 3. Найти числа обратные к числам 4. Вычислить 5. Составить сумму 6. Найти общее решение системы (11.1) по формуле: Примеры. 1) Решить систему сравнений
1. 2. 3. Решим сравнения 4. Вычислим 5. Составим сумму: 6. Найдем общее решение системы: 2) Решить систему сравнений
Прежде всего, приведем данную систему сравнений к виду (11.1). Для этого решим каждое из сравнений системы относительно неизвестной величины x, одним из способов, разобранных выше. Получим систему сравнений, равносильную исходной:
Будем решать полученную систему сравнений по указанному алгоритму. 1. 2. 3. Решим сравнения 4. Вычислим 5. Составим сумму: 6. Найдем общее решение системы:
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 773; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.116 (0.008 с.) |
 , (11.1)
, (11.1)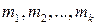 – попарно взаимно просты.
– попарно взаимно просты. , при
, при 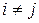 , и пусть числа
, и пусть числа 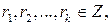 причем
причем 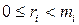 при
при 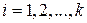 . Тогда существует целое число x, удовлетворяющее системе сравнений (11.1).
. Тогда существует целое число x, удовлетворяющее системе сравнений (11.1).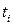 , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям: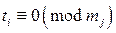 при
при 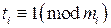 .
. и
и  ,
,  . Это значит, что должно выполняться равенство
. Это значит, что должно выполняться равенство 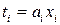 , где
, где  – некоторое целое число. Искомое число
– некоторое целое число. Искомое число 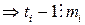 ,
,  , где
, где 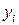 – некоторое целое число.
– некоторое целое число. 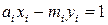 . Поскольку
. Поскольку 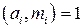 , то, как было установлено в § 6, данное уравнение имеет решение.
, то, как было установлено в § 6, данное уравнение имеет решение. , где
, где 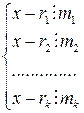 . (11.2)
. (11.2) , где z – некоторое целое число. Докажем, что
, где z – некоторое целое число. Докажем, что 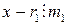 . Имеем
. Имеем
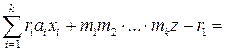

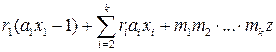 . Каждое из трех слагаемых этой суммы делится на
. Каждое из трех слагаемых этой суммы делится на  . Действительно, поскольку
. Действительно, поскольку  , имеем
, имеем 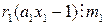 . Так как
. Так как 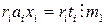 для
для 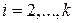 , то и
, то и 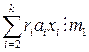 . И, наконец, очевидно, что
. И, наконец, очевидно, что 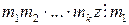 . Следовательно,
. Следовательно, 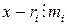 , для
, для 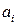 по модулю
по модулю 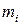 для
для 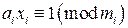 для
для  ;
;  – частное решение системы (11.1).
– частное решение системы (11.1).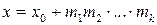 .
.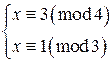 .
. .
. ,
, 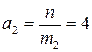 .
. и
и 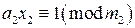 . В нашей задаче это сравнения
. В нашей задаче это сравнения 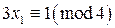 и
и 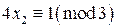 . Получим частные решения этих сравнений:
. Получим частные решения этих сравнений: 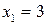 ,
, 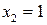 .
.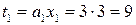 и
и 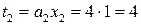 .
. .
. , где
, где 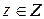 .
.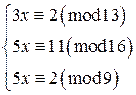 .
.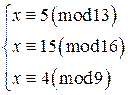 .
.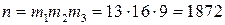 .
. ,
,  ,
, 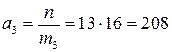 .
.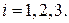 В нашей задаче это сравнения
В нашей задаче это сравнения 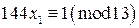 ,
, 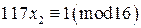 и
и 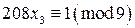 . Получим частные решения этих сравнений:
. Получим частные решения этих сравнений: 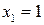 ,
, 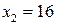 ,
,  .
.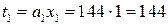 ,
,  и
и 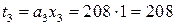 .
.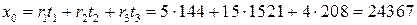 .
. , где
, где  , где
, где 


