
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение сравнений первой степени
Определение 10.1. Сравнением первой степени относительно неизвестного целого числа x называется сравнение вида где a, b и m – целые числа. Если сравнение Пусть Рассмотрим сначала частный случай сравнений первой степени, а именно случай, когда правая часть сравнения равна 1. Определение 10.2. Рассмотрим сравнение Пример. Число 3 обратно к числу 2 по модулю 5, так как Теорема 10.1. Для того, чтобы существовало число x, обратное к числу a по модулю m, необходимо и достаточно, чтобы Доказательство. По теореме 5.1 (признаку взаимной простоты чисел) Как было установлено ранее, числа u и v можно находить при помощи алгоритма Евклида. Значит, алгоритм Евклида можно использовать для нахождения числа, обратного к данному. Пример. Найти число, обратное к 26 по модулю 49. Решим сравнение Поскольку
Последний, отличный от 0, остаток и равен 1. Найдем его линейное представление:
Итак, получили, что Тогда Вернемся теперь к общему случаю сравнения: Теорема 10.2. Пусть Доказательство. 1) Необходимость. Пусть сравнение где 2) Достаточность. Пусть
Теорема 10.2 указывает путь к решению сравнений первой степени. Действительно, решение сравнения первой степени можно свести к решению неопределенного уравнения. Пример. Решить сравнение Другой способ решения сравнений первой степени состоит в применении теоремы Эйлера. Рассмотрим сравнение Тогда по теореме Эйлера Пример. Решить сравнение Итак, мы рассмотрели два способа решения сравнений. Первый способ сводит решение сравнения к решению неопределенного уравнения. Используя второй способ, мы можем наоборот свести решение неопределенного уравнения к решению сравнения. Рассмотрим неопределенное уравнение
Пример. Решить уравнение
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 3761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.106.203 (0.009 с.) |
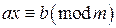 , (10.1)
, (10.1)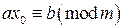 верно, то число
верно, то число  называется частным решением сравнения.
называется частным решением сравнения. , где
, где  , очевидно, также является частным решением данного сравнения, а множество частных решений вида
, очевидно, также является частным решением данного сравнения, а множество частных решений вида 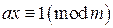 . Любое частное решение этого сравнения называется числом, обратным к числу a по модулю m.
. Любое частное решение этого сравнения называется числом, обратным к числу a по модулю m.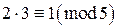 . Число
. Число 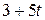 также является обратным к числу 2 по модулю 5 при любом целом t.
также является обратным к числу 2 по модулю 5 при любом целом t.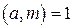 .
. , для которых выполняется
, для которых выполняется  . Это равенство можно записать в виде:
. Это равенство можно записать в виде:  . Это и означает, что число u обратно к a по модулю m.
. Это и означает, что число u обратно к a по модулю m. .
. , искомое число существует. Найдем НОД чисел 26 и 49, (который, как мы знаем, равен 1), по алгоритму Евклида.
, искомое число существует. Найдем НОД чисел 26 и 49, (который, как мы знаем, равен 1), по алгоритму Евклида.
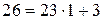
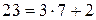


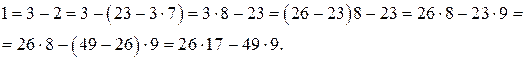
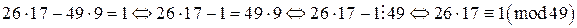 .
. – частное решение сравнения
– частное решение сравнения 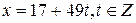 . Все числа такого вида и будут числами, обратными к 26 по модулю 49.
. Все числа такого вида и будут числами, обратными к 26 по модулю 49.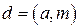 . Для того, чтобы сравнение (10.1) имело решение, необходимо и достаточно, чтобы
. Для того, чтобы сравнение (10.1) имело решение, необходимо и достаточно, чтобы  .
.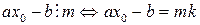 , где k – целое число. Поскольку
, где k – целое число. Поскольку 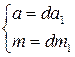 ,
,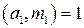 . Тогда
. Тогда  . Поскольку
. Поскольку 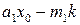 – целое число,
– целое число,  . Поскольку
. Поскольку  и
и  :
:  . Умножим обе части равенства на d, получим
. Умножим обе части равенства на d, получим 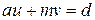 , затем умножим обе части полученного равенства на k, получим
, затем умножим обе части полученного равенства на k, получим  . Отсюда следует, что
. Отсюда следует, что 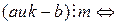
 . Значит, сравнение
. Значит, сравнение 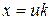 .
.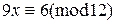 . Решение этого сравнения существует, поскольку
. Решение этого сравнения существует, поскольку 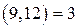 и
и  . Запишем сравнение в виде
. Запишем сравнение в виде 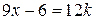 , где
, где 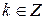
 . Решим полученное неопределенное уравнение при помощи алгоритма Евклида, получим частное решение
. Решим полученное неопределенное уравнение при помощи алгоритма Евклида, получим частное решение 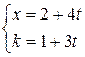 , где
, где  , где
, где  и
и  , то по теореме 10.2 для существования решения сравнения необходимо и достаточно, чтобы
, то по теореме 10.2 для существования решения сравнения необходимо и достаточно, чтобы 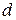 . При этом частные от делений чисел a и m будут взаимно просты. Поэтому можно изначально предполагать, что
. При этом частные от делений чисел a и m будут взаимно просты. Поэтому можно изначально предполагать, что 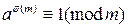 . Умножим обе части сравнения на число b, получим
. Умножим обе части сравнения на число b, получим 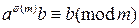 . Запишем последнее сравнение в виде
. Запишем последнее сравнение в виде 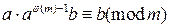 . Число
. Число  , очевидно, является частным решением сравнения. Общее решение сравнения имеет вид:
, очевидно, является частным решением сравнения. Общее решение сравнения имеет вид: 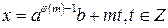 .
.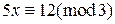 . Поскольку
. Поскольку 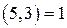 , по теореме Эйлера
, по теореме Эйлера 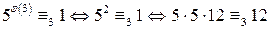 . Положим
. Положим 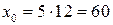 . Найденное значение
. Найденное значение 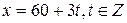 . Заменим
. Заменим 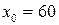 на число, сравнимое с ним по модулю 3 и запишем ответ в упрощенном виде:
на число, сравнимое с ним по модулю 3 и запишем ответ в упрощенном виде:  .
.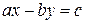 . Предположим, что
. Предположим, что 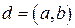 и
и 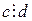 . Тогда, как было установлено в § 6, данное уравнение имеет решение. Запишем уравнение в виде
. Тогда, как было установлено в § 6, данное уравнение имеет решение. Запишем уравнение в виде 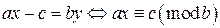 . Решив сравнение при помощи функции Эйлера, найдем частное решение
. Решив сравнение при помощи функции Эйлера, найдем частное решение 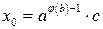 . Подставив его в уравнение, найдем частное решение
. Подставив его в уравнение, найдем частное решение 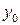 , а затем выпишем общее решение уравнения.
, а затем выпишем общее решение уравнения.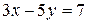 . Из уравнения получим сравнение
. Из уравнения получим сравнение 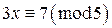 . Поскольку
. Поскольку  , сравнение имеет решение. Тогда
, сравнение имеет решение. Тогда 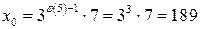 – частное решение сравнения. Упростим его, получим
– частное решение сравнения. Упростим его, получим 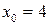 . Общее решение сравнения
. Общее решение сравнения  ,
,  . Тогда частное решение
. Тогда частное решение 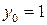 , а общее решение
, а общее решение  ,
,  ,
, 


