
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление нод. Алгоритм Евклида
Алгоритм Евклида дает возможность вычислить наибольший общий делитель для любых двух целых чисел. Для описания алгоритма рассмотрим следующие две леммы. Лемма 1. Если Доказательство. Очевидно, что Лемма 2. Пусть Доказательство. Пусть Пусть Если два числовых множества совпадают, то совпадают их наибольшие по величине элементы, что и доказывает лемму.
Сформулируем теперь алгоритм Евклида. Рассмотрим два целых числа Шаг 1. Разделим Если число Шаг 2. Разделим Если Продолжая процесс деления, получим последовательность остатков – убывающую последовательность целых неотрицательных чисел, вычисляемых по следующим рекуррентным формулам: Поскольку такая последовательность не может иметь бесконечно много членов, на некотором шаге очередной остаток окажется равным нулю. Тогда последний, отличный от нуля остаток и есть НОД чисел Пример. Найдем НОД чисел Далее, разделим Продолжим процесс деления:
Таким образом, последний отличный от В следующей теореме утверждается, что наибольший общий делитель двух чисел можно представить в виде линейной комбинации этих чисел с целыми коэффициентами. Теорема 4.1. (линейное представление НОД) Рассмотрим два целых числа Доказательство. Докажем, что каждый из остатков
База индукции. Пусть Индукционный переход. Пусть утверждение справедливо для всех натуральных чисел Из алгоритма Евклида следует, что
По индукционному предположению
Следовательно, Положим Пример. В предыдущем примере был найден НОД чисел
Итак, получили, что
Взаимно простые числа Определение 5.1. Целые числа
Примеры. 1. Числа 2. Числа Следующая теорема устанавливает необходимое и достаточное условие взаимной простоты чисел. Теорема 5.1 (признак взаимной простоты чисел). Для того, чтобы числа Доказательство. 1. Необходимость. Пусть числа 2. Достаточность. Пусть справедливо утверждение Следствие 1. Если числа Доказательство. По теореме из взаимной простоты чисел
Следствие 2. Рассмотрим целые числа Доказательство. По теореме условие следующем виде: Поскольку
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.102.90 (0.022 с.) |
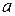
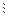
 , то
, то  .
.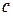 – общий делитель чисел
– общий делитель чисел 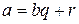 , причем числа
, причем числа 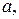
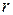 отличны от 0 и
отличны от 0 и  . Тогда
. Тогда 
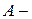 множество общих делителей чисел
множество общих делителей чисел 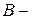 множество общих делителей чисел
множество общих делителей чисел 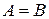 .
.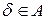 , это значит, что
, это значит, что 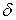 и
и 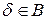 , следовательно,
, следовательно, 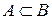 . Аналогично докажем, что
. Аналогично докажем, что 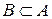 . Из определения равенства двух множеств получим, что
. Из определения равенства двух множеств получим, что  Требуется найти наибольший общий делитель чисел
Требуется найти наибольший общий делитель чисел 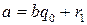 , где
, где  . Тогда по лемме 2
. Тогда по лемме 2 
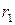 . Если
. Если 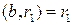 (по лемме 1). Тогда
(по лемме 1). Тогда  .
. , где
, где 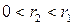 . Тогда по лемме 2
. Тогда по лемме 2 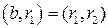 , а значит, справедливо и
, а значит, справедливо и 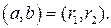
 .
.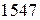 и
и 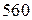 . Для этого разделим
. Для этого разделим  . Таким образом, первый полученный остаток
. Таким образом, первый полученный остаток  .
.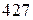 , получим
, получим  , при этом
, при этом 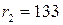 .
. ,
, 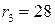 ;
;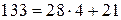 ,
, 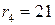 ;
;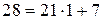 ,
, 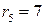 ;
;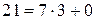 ,
, 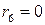 .
.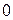 остаток равен
остаток равен  , это и есть наибольший общий делитель чисел
, это и есть наибольший общий делитель чисел 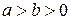 ,
, 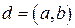 . Тогда найдутся такие целые числа
. Тогда найдутся такие целые числа 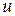 и
и 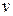 , что
, что  .
.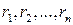 , полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел
, полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел 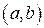 . Будем доказывать это утверждение методом математической индукции.
. Будем доказывать это утверждение методом математической индукции. . Имеем
. Имеем 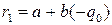 . Получили, что остаток
. Получили, что остаток 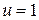 и
и  .
.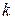 , не превосходящих
, не превосходящих  :
:  , при
, при 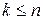 . Докажем, что это утверждение справедливо также для
. Докажем, что это утверждение справедливо также для 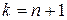 .
.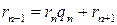

 .
. и
и 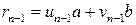 .
. 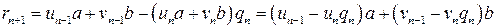 .
. и
и 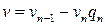 . Тогда
. Тогда  , что и требовалось установить.
, что и требовалось установить. . Найдем его линейное представление:
. Найдем его линейное представление:
 , т. е. представили НОД чисел
, т. е. представили НОД чисел 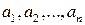 называются взаимно простыми, если их НОД равен
называются взаимно простыми, если их НОД равен  :
: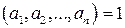
 и
и 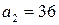 – взаимно простые.
– взаимно простые.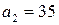 – не взаимно простые, так как
– не взаимно простые, так как 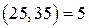 .
.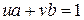 .
. . Тогда по теореме о линейном представлении НОД найдутся такие целые числа
. Тогда по теореме о линейном представлении НОД найдутся такие целые числа 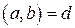 , причем
, причем  . Тогда
. Тогда 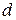 и
и 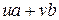
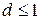 . Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо
. Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо  и
и 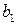 , то числа
, то числа 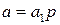 ,
,  , где
, где 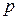 и
и 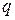 – целые числа. Тогда
– целые числа. Тогда 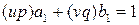 , а, значит, числа
, а, значит, числа 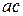
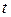 , что
, что  . Умножим обе части последнего равенства на
. Умножим обе части последнего равенства на 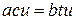 . Но
. Но  , тогда
, тогда .
.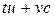 – целое число, последнее равенство означает, что
– целое число, последнее равенство означает, что 


