
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление рациональных чисел конечными цепными
дробями Определение 12.1. Целой частью числа a называется наибольшее целое число, не превосходящее a. Целая часть числа a обозначается Каждое рациональное число можно представить в виде отношения двух целых чисел: Шаг 1. Разделим a на b с остатком: где Шаг 2. Разделим b на где Шаг 3. Разделим где Будем продолжать процесс до тех пор, пока на очередном шаге остаток не станет равным нулю. Заметим, что на некотором шаге это должно произойти, так как последовательность остатков – это убывающая последовательность натуральных чисел, а такая последовательность не может содержать бесконечное число членов. Предположим, что остаток с номером Шаг n. Разделим где Шаг где Вернемся теперь к началу процесса. Из равенства (12.4) получим Тогда из равенства (12.2) можно получить: Из равенства (12.6) получим
Тогда из равенства (12.12) можно получить: Продолжая этот процесс, получим равенство Определение 12.2. Выражение вида Числа Сокращенная запись цепной дроби: В рассмотренном выше процессе мы представили обыкновенную дробь Теорема 12.1. Всякое рациональное число может быть представлено в виде конечной цепной дроби, причем единственным образом. Доказательство. 1) Пусть q – рациональное число. Из определения рационального числа следует, что каждое рациональное число можно записать в виде отношения двух целых взаимно простых чисел, то есть в виде обыкновенной несократимой дроби. Пусть Рассмотрим сначала случай, когда Рассмотрим случай, когда Таким образом, установлено, что любая обыкновенная дробь может быть представлена в виде цепной дроби. Заметим, что целое число, само является своей цепной дробью: если 2) Единственность представления рационального числа в виде цепной дроби следует из того, что при построении цепной дроби на каждом шаге вычисляются неполные частные при делении двух чисел с остатком, которые определяются единственным образом. Теорема доказана. Из доказательства теоремы 12.1 можно сделать вывод о том, что в цепной дроби Примеры. 1) Представить число
Получим неполные частные 2) Представить число
Получим неполные частные 3) Представить число
Замечание. Последнее неполное частное в цепной дроби всегда больше 1. Действительно, если предположить, что Из этого замечания следует, что каждую цепную дробь
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.177.14 (0.012 с.) |
 .
. , где
, где 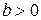 ,
, 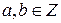 , причем, при условии, что дробь
, причем, при условии, что дробь 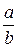 – несократима, такое представление единственно. Пусть
– несократима, такое представление единственно. Пусть  . Применим к числам a и b алгоритм Евклида:
. Применим к числам a и b алгоритм Евклида: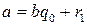 , (12.1)
, (12.1)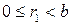 . Если остаток
. Если остаток 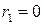 , то процесс закончен. Предположим, что
, то процесс закончен. Предположим, что  . Разделим обе части (12.1) на b, получим
. Разделим обе части (12.1) на b, получим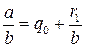 . (12.2)
. (12.2)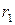 :
: , (12.3)
, (12.3)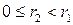 . Если остаток
. Если остаток 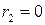 , то процесс закончен. Предположим, что
, то процесс закончен. Предположим, что  . Разделим обе части (12.3) на
. Разделим обе части (12.3) на 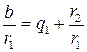 . (12.4)
. (12.4)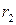 :
: , (12.5)
, (12.5)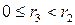 . Если
. Если 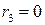 , то процесс закончен. Предположим, что
, то процесс закончен. Предположим, что  . Разделим обе части (12.5) на
. Разделим обе части (12.5) на  . (12.6)
. (12.6) окажется равным нулю. Тогда процесс закончится на шаге с номером
окажется равным нулю. Тогда процесс закончится на шаге с номером  на
на 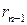 :
: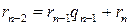 , (12.7)
, (12.7)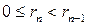 , при этом
, при этом 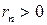 . Разделим обе части (12.7) на
. Разделим обе части (12.7) на  . (12.8)
. (12.8)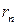 :
: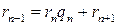 , (12.9)
, (12.9)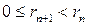 . Мы предположили, что
. Мы предположили, что 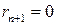 . Разделим обе части (12.9) на
. Разделим обе части (12.9) на 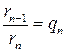 . (12.10)
. (12.10)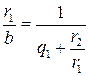 . (12.11)
. (12.11) . (12.12)
. (12.12)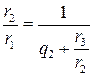 . (12.13)
. (12.13)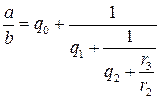 .
. . (12.14)
. (12.14) , где
, где 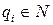 ,
, 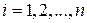 называется конечной цепной дробью.
называется конечной цепной дробью.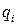 при
при  называются неполными частными.
называются неполными частными. .
.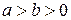 . В этом случае неполное частное
. В этом случае неполное частное 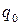 является целой частью числа
является целой частью числа  .
. , где
, где  .
. . Если при этом
. Если при этом 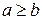 , то, как было установлено выше, используя алгоритм Евклида, можно представить дробь
, то, как было установлено выше, используя алгоритм Евклида, можно представить дробь 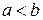 , то, первый шаг в алгоритме Евклида будет иметь вид:
, то, первый шаг в алгоритме Евклида будет иметь вид: 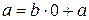 . Здесь
. Здесь 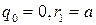 . Продолжая процесс, получим
. Продолжая процесс, получим 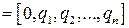 .
. . Тогда дробь
. Тогда дробь 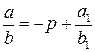 , где
, где  ,
,  . Представим дробь
. Представим дробь 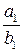 в виде цепной дроби:
в виде цепной дроби:  .
.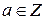 , то
, то  , в частности,
, в частности, 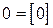 .
. , а
, а 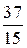 в виде цепной дроби. Применим к числам 37 и 15 алгоритм Евклида:
в виде цепной дроби. Применим к числам 37 и 15 алгоритм Евклида: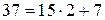 ,
, ,
,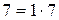 .
.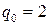 ,
, 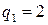 ,
, 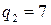 . Тогда
. Тогда  .
.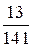 в виде цепной дроби. Целая часть этого числа равна 0, тогда
в виде цепной дроби. Целая часть этого числа равна 0, тогда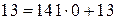 ,
, ,
,
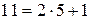 ,
, .
.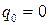 ,
,  ,
, 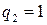 ,
,  ,
,  . Тогда
. Тогда 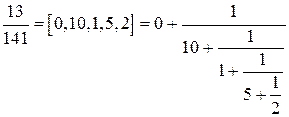 .
.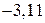 в виде цепной дроби. Целая часть этого числа равна
в виде цепной дроби. Целая часть этого числа равна 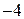 . Запишем это число в виде
. Запишем это число в виде 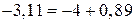 . Тогда, как это было сделано в примере 2, представим число
. Тогда, как это было сделано в примере 2, представим число  в виде:
в виде: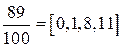 . Значит,
. Значит,  .
. , то по формуле (12.9), учитывая, что
, то по формуле (12.9), учитывая, что 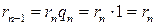 . Но по определению деления с остатком,
. Но по определению деления с остатком,  . Значит, предположение о том, что
. Значит, предположение о том, что 
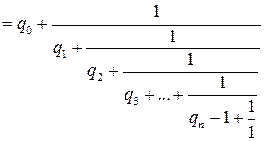 .
.


