Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимые и независимые случайные величины
Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина. Для независимых случайных величин условные плотности распре- деления равны их безусловным плотностям, то есть
В частности, для непрерывных двумерных случайных величин
Пример. Имеются две независимые непрерывные случайные величины X и Y, подчиненные каждая показательному закону
Найти: а) плотность распределения системы; б) интегральную функцию распределения системы. Решение. а) б) Итак, Количественными числовыми характеристиками системы двух случайных величин являются так называемые начальные и центральные моменты различных порядков, прежде всего, математическое ожидание, дисперсия и корреляционный момент. Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения
в частности, Центральным моментом порядка k, s системы (X, Y) называется математическое ожидания произведения центрированных величин:
в частности, Формулы для непосредственного подсчета моментов являются обобщением соответствующих формул для одномерных случайных величин. Для дискретных двумерных случайных величин
Для непрерывных двумерных случайных величин
Особую роль как характеристика системы играет второй смешанный центральный момент
Для дискретных двумерных случайных величин
Для непрерывных двумерных случайных величин
Корреляционный момент помимо рассеивания случайных величин X и Y характеризует зависимость между ними. Для независимых случайных величин X и Y Если
На практике для характеристики связи между случайными величинами удобно использовать безразмерную величину
называемую коэффициентом корреляции. Можно показать, что Коэффициент корреляции служит для характеристики степени тесноты линейной зависимости между случайными величинами. В предельном случае когда величины X и Y связаны между собой линейной функциональной зависимостью Пример. Непрерывная двумерная случайная величина (X, Y) задана плотностью распределения Решение.
Из условия симметрии функции
Следовательно, величины X и Y некоррелированны.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.107.90 (0.006 с.) |
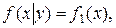
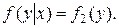 Поэтому необходимое и достаточное условие независимости случайных величин X и Y состоит в том, что для них интегральная функция распределения двумерной случайной величины (X, Y) равна произведению функций распределения составляющих
Поэтому необходимое и достаточное условие независимости случайных величин X и Y состоит в том, что для них интегральная функция распределения двумерной случайной величины (X, Y) равна произведению функций распределения составляющих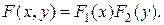
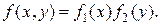
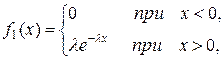
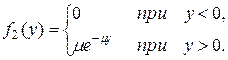
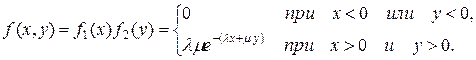
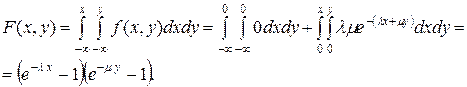
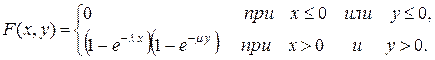
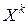 на
на 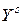 :
: 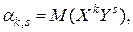
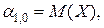
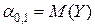 - математические ожидания составляющих системы.
- математические ожидания составляющих системы.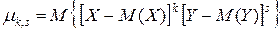 ,
,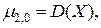
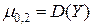 - дисперсии составляющих X и Y, характеризующие рассеивание случайной точки в направлении осей Ox и Oy.
- дисперсии составляющих X и Y, характеризующие рассеивание случайной точки в направлении осей Ox и Oy.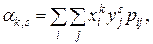
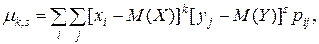
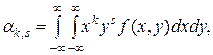
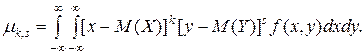
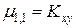 , называемый корреляционным моментом (или моментом связи):
, называемый корреляционным моментом (или моментом связи):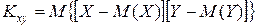 .
.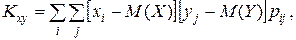
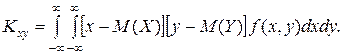
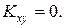 Случайные величины, для которых
Случайные величины, для которых 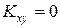 , называются некоррелированными.
, называются некоррелированными.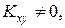 то это есть признак наличия зависимости между ними.
то это есть признак наличия зависимости между ними.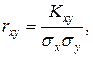
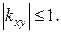
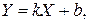 то
то 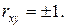
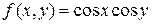 в квадрате
в квадрате 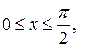
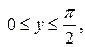 вне его
вне его 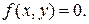 Найти математические ожидания и дисперсии составляющих. Доказать, что величины X и Y некоррелированны.
Найти математические ожидания и дисперсии составляющих. Доказать, что величины X и Y некоррелированны.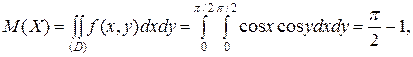
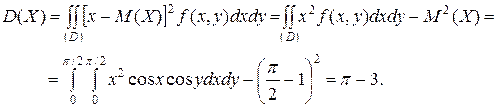
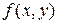 следует, что
следует, что