
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределения
Непрерывная случайная величина подчинена нормальному закону распределения (закону распределения Гаусса), если ее плотность вероят-ностей равна
Здесь
Нормальное распределение с параметрами
Эта функция табулирована (см. Приложение 1). График плотности вероятностей нормально распределенной случайной величины (называемый нормальной или гауссовой кривой) показан на рисунке.
Вероятность попадания нормально распределенной случайной вели-чины на произвольный конечный интервал (
где Вероятность попадания нормально распределенной случайной вели-чины на интервал, симметричный относительно среднего значения, равна В частности, при Если случайная величина распределена по нормальному закону, то с вероятностью, близкой к достоверности, можно считать, что практи-чески все рассеивание укладывается на интервале Пример. На станке изготовляется партия однотипных деталей. Длина детали X - случайная величина, распределенная по нормальному закону с параметрами вероятность того, что длина наудачу взятой детали заключена между 17,7 см и 18,4 см; какое отклонение длины детали от номинального размера можно гарантировать с вероятностью 0,95? В каких пределах будут за-ключены практически все длины деталей? Решение.
Воспользуемся формулой Следовательно, По правилу трех сигм можно считать, что практически все длины деталей с вероятностью 0,9973 будут заключены в интервале Пример. Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожи-данием (проектной длиной), равным 60 мм. Фактическая длина изготов-ленных деталей не менее 58 мм и не более 62 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 61 мм; б) меньше 60,5 мм.
Решение. Предварительно найдем неизвестный параметр нормального распределения
откуда Следовательно,
Задачи для самостоятельного решения 1. В коробке, содержащей 10 дискет, три заполнены некоторой информацией, остальные – “чистые”. Наудачу вынуты четыре дискеты. Составить закон распределения числа заполненных дискет среди отобранных. 2. Построить ряд распределения случайной величины X - суммы очков, выпадающих при бросании двух игральных костей; найти среднее значение этой суммы. 3. Построить ряд распределения случайной величины Y – произведения очков, выпадающих при бросании двух игральных костей; найти среднее значение этой суммы. 4. Имеются 5 различных ключей, из которых только один подходит к замку. Составить закон распределения числа опробованных ключей, если опробованный ключ в последующих попытках не используется. 5. Два стрелка стреляют каждый по своей мишени, делая независимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка 6. В лотерее на 100 билетов разыгрываются 2 выигрыша на сумму 1000 и 100 рублей. Стоимость билета – 10 рублей. Составить закон распределения суммы чистого выигрыша S для лица, имеющего два билета. 7. Имеются семь биллиардных шаров, перенумерованных числами от 1 до 7. Эти шары располагаются случайным образом вдоль борта. Найти закон распределения и математическое ожидание числа шаров с четными номерами, предшествующих первому в последовательности шару с нечетным номером. 8. Написать закон распределения вероятностей числа переключений передач при трех заездах автомобиля, если вероятность переключения
9. Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях равно 30. 10. Два баскетболиста по очереди бросают мяч в корзину. Вероятность попадания при каждом броске для первого баскетболиста равна 0,8; для второго 0,7. Составить закон распределения общего числа попаданий. 11. В авторалли участвуют 25 машин. Вероятность того, что машина не дойдет до финиша равна 0,2. Найти вероятность того, что число машин, не дошедших до финиша, будет отличаться от своего математического ожидания не более чем на одно среднее квадратическое отклонение. 12. Случайные величины X и Y независимы. Найти среднее квадратическое отклонение случайной величины 13. При сборке прибора для наиболее точной подгонки основной детали может потребоваться (в зависимости от удачи) 1, 2, 3, 4 или 5 проб соответственно с вероятностями 0,1, 0,2, 0,5, 0,15, 0,05. Требуется обеспечить сборщика необходимым количеством деталей для сборки 20 приборов. Сколько деталей надо отпустить сборщику? 14. Непрерывная случайная величина задана плотностью вероятностей
(закон распределения Коши). Найти: коэффициент a, интегральную функцию распределения 15. Непрерывная случайная величина задана плотностью вероятностей (закон распределения Релея – применяется в радиотехнике). Найти: M (x), D (x). 16. Непрерывная случайная величина задана интегральной функцией распределения где распределения Вейбулла – часто применяется в теории надежности тех- нических систем, в статистической теории прочности). Найти: плот- ность 17. Непрерывная случайная величина задана плотностью вероятностей (гамма – распределение) Найти: M (x), D (x). 18. Непрерывная случайная величина задана плотностью вероятностей
Лапласа). Найти: коэффициент a; интегральную функцию распределе- ния 19. Точка брошена наудачу внутрь круга радиуса R. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади этой области. Найти интегральную функцию распределения 20. Найти среднее число лотерейных билетов, на которые выпадут выигрыши, если приобретено 50 билетов, причем вероятность выигрыша по одному билету равна 0,02. 21. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 4 мин поступит: а) три вызова; б) менее трех вызовов; в) не менее трех вызовов. 22. Среднее число автомобилей, подъезжающих к стоянке за один час, равно 4. Найти вероятность того, что за 2,5 часа к стоянке подъедут более 8 автомашин. 23. Через железнодорожный переезд в течение 10 мин в среднем проходит 2 поезда. Найти вероятность того, что за полчаса переезд будет закрываться: а) три раза; б) не более двух раз; в) не будет закрываться вообще.
24. Гидравлическая система автомобиля насчитывает 100 клапанов. Надежность каждого клапана 0,98. Какова вероятность того, что за время испытания откажут не менее двух клапанов, если считать отказ каждого из них независимым от состояния других. 25. По каналу связи передают 1000 знаков Каждый знак может быть искажен независимо от других с вероятностью 0,003. Найти вероятность того, что будет искажено не более трех знаков. 26. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,005. Найти наиболее вероятное число опоздавших пассажиров из 600 и его вероятность. 27. При движении по проселочной дороге автомобиль испытывает в среднем 60 толчков в течение одного часа. Какова вероятность того, что за 30 сек. не будет ни одного толчка? 28. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время осмотра, распределяется по закону Пуассона с параметром a. Если неисправностей не обнаружено, техническое обслуживание машины продолжается в среднем 2 часа. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 часа. Составить закон распределения среднего времени обслуживания T и ремонта машины и его математическое ожидание M (T). 29. На пути движения автомашины 4 светофора. Каждый из них либо запрещает дальнейшее движение автомашине с вероятностью 0,4, либо разрешает движение с вероятностью 0,6. Построить ряд распределения случайной величины X -пройденных автомашиной светофоров до первой остановки. 30. Автоматическая линия при нормальной настройке может выпускать бракованное изделие с вероятностью p. Переналадка линии производится сразу после первого же бракованного изделия. Найти среднее число всех изделий, изготовляемых между двумя переналадками линии. 31. Проводится испытание трех приборов, работающих независимо один от другого. Длительность времени безотказной работы приборов распределена по показательному закону: для первого прибора
32. На дороге находится контрольный пункт для проверки технического состояния автомашин. Найти математическое ожидание и среднее квадратическое отклонение случайной величины T – времени ожидания очередной машины контролером, если поток машин простейший и время (в часах) между прохождениями машин через контрольный пункт распределено по показательному закону 33. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения – 10 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее трех минут и среднее время ожидания автобуса. 34. Ребро куба x измерено приближенно, причем 35. Колесу придается вращение, которое затухает вследствие трения. Фиксированный радиус R при этом, останавливаясь, образует с горизонтом случайный угол 36. На перекрестке стоит автоматический светофор, в котором 1 мин. горит зеленый свет, 0,5 мин. – красный, затем опять 1 мин. – зеленый, 0,5 мин. – красный и т.д. Некто подъезжает к перекрестку на машине в случайный момент времени, не связанный с работой светофора. Найти: а) вероятность того, что он проедет перекресток, не останавливаясь; б) закон распределения и математическое ожидание времени ожидания у перекрестка. 37. Автомат изготовляет подшипники, которые считаются годными, если отклонение X от проектного размера по абсолютной величине не превосходит 0,77 мм. Каково наиболее вероятное число годных подшипников из 100, если X распределена нормально с 38. Случайная величина X подчинена нормированному нормальному распределению ( 39. Производится взвешивание некоторого вещества без систематических (одного знака) погрешностей. Случайные погрешности взвешивания подчинены нормальному закону распределения со средним квадратическим отклонением 40. Случайная величина X подчинена нормальному закону распределения с параметрами 41. Случайные ошибки измерения подчинены нормальному закону распределения с параметрами 42. Диаметр отверстия X - случайная величина, распределенная по нормальному закону с параметрами
43. Браковка шариков для подшипников производится следующим образом: если шарик не проходит через отверстие диаметром 44. При 10000 бросаний монеты герб выпал 5500 раз. Следует ли считать, что монета несимметрична? Ответы 1.
2.
3.
4. 5.
6. 7.
10. 11.
1 4. функция. 17. 18. 19. случайная величина до центра круга. 17. 1. 18. а) 0,0256; б) 0,0123; в) 0,9877. 22. 2 5. 0,647. 2 6. 0,224. 2 7. 2 8.
2 9.
30.
31. а) 32.
36. Поэтому 3 8. 40. 0,0633. 41. 0,398. 42. 0,6915. 4 3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 598; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.17 (0.052 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
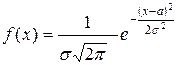 .
.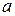 и
и  -параметры, вероятностный смысл которых таков:
-параметры, вероятностный смысл которых таков: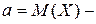 математическое ожидание.
математическое ожидание.  - среднее квадратиче-ское отклонение нормально распределенной случайной величины X.
- среднее квадратиче-ское отклонение нормально распределенной случайной величины X.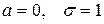 называется нормированным. Плотность вероятностей нормированного нормального распределения равна
называется нормированным. Плотность вероятностей нормированного нормального распределения равна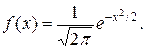

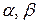 ) равна
) равна
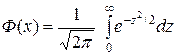 - функция Лапласа (см. приложение 2).
- функция Лапласа (см. приложение 2).
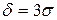
 Поэтому вероятность противоположного события:
Поэтому вероятность противоположного события: 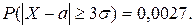
 Такой малой вероятностью можно пренебречь. На этом и базируется важное для приложений правило трех сигм:
Такой малой вероятностью можно пренебречь. На этом и базируется важное для приложений правило трех сигм: 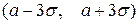 от центра распределения, то есть можно пренебречь вероятностью попада-ния случайной величины вне интервала
от центра распределения, то есть можно пренебречь вероятностью попада-ния случайной величины вне интервала  .
.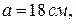
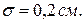 Найти:
Найти: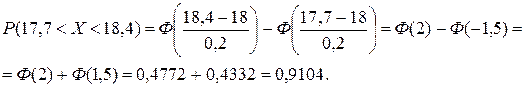
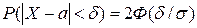 . По условию
. По условию  . Поэтому
. Поэтому  или
или  По таблице функции Лапласа (см. приложение 2) находим
По таблице функции Лапласа (см. приложение 2) находим  , откуда
, откуда 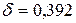 .
.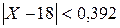 или
или 
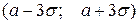 , т.е.
, т.е. 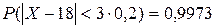 , откуда
, откуда  .
.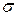 из условия
из условия 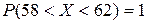 или
или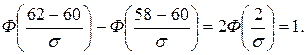
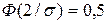 и по таблицам функции Лапласа находим
и по таблицам функции Лапласа находим 
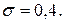 Поэтому
Поэтому 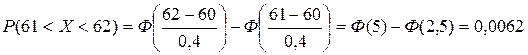 ,
, .
.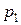 , для второго
, для второго 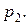 Построить ряд распределения случайной величины
Построить ряд распределения случайной величины  где
где 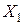 - число попаданий первого стрелка,
- число попаданий первого стрелка, 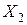 - число попаданий второго стрелка. Найти
- число попаданий второго стрелка. Найти 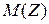 и
и 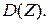
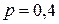 (считать, что в одном заезде одно переключение). Найти среднее значение числа переключений.
(считать, что в одном заезде одно переключение). Найти среднее значение числа переключений.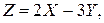 если известно, что
если известно, что 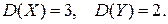
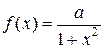
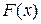 ,
, 

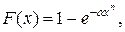
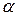 - некоторая константа, n – целое положительное число (закон
- некоторая константа, n – целое положительное число (закон  M (x) и D (x).
M (x) и D (x). 
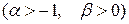 .
.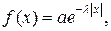 где
где  - положительный параметр (закон распределения
- положительный параметр (закон распределения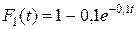 , для второго -
, для второго - 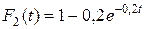 , для третьего
, для третьего  . Найти вероятность того, что в течение пяти часов откажут: а) только один прибор; б) два прибора; в) все три прибора; г) хотя бы один прибор; д) не менее двух приборов.
. Найти вероятность того, что в течение пяти часов откажут: а) только один прибор; б) два прибора; в) все три прибора; г) хотя бы один прибор; д) не менее двух приборов.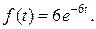
 Рассматривая длину ребра как случайную величину, распределенную равномерно в интервале
Рассматривая длину ребра как случайную величину, распределенную равномерно в интервале 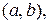 найти математическое ожидание и дисперсию объема куба.
найти математическое ожидание и дисперсию объема куба.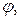 который распределяется по равномерному закону в пределах от 0° до 360°. Определить математическое ожидание и среднее квадратическое отклонение расстояния конца радиуса от горизонтального диаметра.
который распределяется по равномерному закону в пределах от 0° до 360°. Определить математическое ожидание и среднее квадратическое отклонение расстояния конца радиуса от горизонтального диаметра.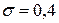 мм?
мм?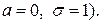 Что больше:
Что больше: 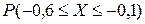 или
или 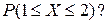
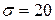 г. Найти вероятность того, что взвешивание будет произведено с погрешностью, не превосходящей по абсолютной величине 10 г.
г. Найти вероятность того, что взвешивание будет произведено с погрешностью, не превосходящей по абсолютной величине 10 г.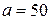 мм и
мм и 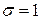 мм. Найти вероятность того, что X попадет на интервал (49,5; 50,2) не менее трех раз при четырех независимых испытаниях?
мм. Найти вероятность того, что X попадет на интервал (49,5; 50,2) не менее трех раз при четырех независимых испытаниях?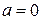 и
и 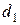 , но проходит через отверстие
, но проходит через отверстие 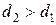 , то его размер считается приемлемым. Если какое – либо из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика D есть нормальная случайная величина с
, то его размер считается приемлемым. Если какое – либо из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика D есть нормальная случайная величина с 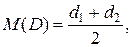
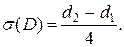 Найти вероятность того, что шарик будет забракован. Какова вероятность того, что из восьми шариков менее двух будут забракованы?
Найти вероятность того, что шарик будет забракован. Какова вероятность того, что из восьми шариков менее двух будут забракованы?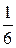
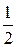
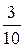
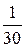

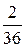
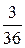
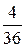

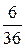
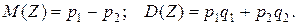
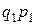
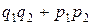

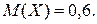
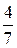

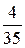

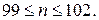
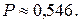 12.
12. 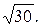 13. 57.
13. 57.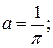

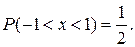 15.
15. 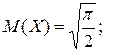
 16.
16. 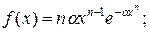
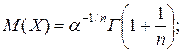
 где
где  - гамма-
- гамма-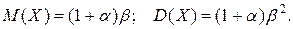 Указание: Сделать подстановку
Указание: Сделать подстановку 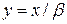 и использовать гамма – функцию.
и использовать гамма – функцию.

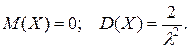
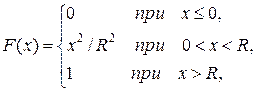
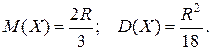 Здесь
Здесь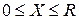 - расстояние от произвольной точки
- расстояние от произвольной точки  2 3. а) 0,0890; б) 0,0620; в) 0,0025. 2 4. 0,366.
2 3. а) 0,0890; б) 0,0620; в) 0,0025. 2 4. 0,366. 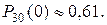


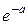
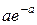
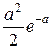
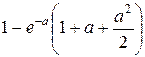
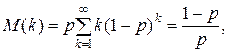 где случайная величина k – число годных изделий, изготовляемых линией до появления брака. Указание: Для вычисления суммы можно воспользоваться известным равенством:
где случайная величина k – число годных изделий, изготовляемых линией до появления брака. Указание: Для вычисления суммы можно воспользоваться известным равенством: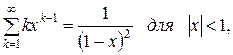 получающимся путем дифференцирования суммы бесконечно убывающей геометрической прогрессии
получающимся путем дифференцирования суммы бесконечно убывающей геометрической прогрессии 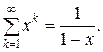
 б)
б) 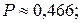 в)
в) 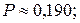 г)
г) 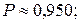 д)
д) 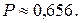
 часа. Указание: время ожидания машины контролером и время прохождения машин через контрольный пункт распределены одинаково. 33.
часа. Указание: время ожидания машины контролером и время прохождения машин через контрольный пункт распределены одинаково. 33. 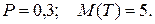 34.
34. 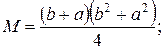
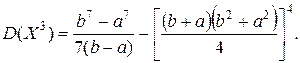 35.
35. 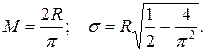
 Указание: момент проезда машины через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре, то есть 1,5 мин. Время ожидания
Указание: момент проезда машины через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре, то есть 1,5 мин. Время ожидания  - смешанная случайная величина: с вероятностью 2/3 она равна 0, а с вероятностью 1/3 она может принимать с одинаковой плотностью вероятности любое значение между 0 и 0,5 мин.
- смешанная случайная величина: с вероятностью 2/3 она равна 0, а с вероятностью 1/3 она может принимать с одинаковой плотностью вероятности любое значение между 0 и 0,5 мин.  37.
37. 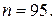
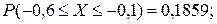
 3 9. 0,383.
3 9. 0,383.
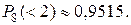 4 4. Почти наверняка. Указание: применить правило “трех сигм”.
4 4. Почти наверняка. Указание: применить правило “трех сигм”.


