
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в нечёткой постановке
3.1. Понятие о нечётком множестве Формально определим нечёткие множества. Допустим Х = {x} – множество объектов или точек, обозначенных через Х. Например, Х может быть множеством всех действительных чисел. Это множество называется универсальным. Нечёткое, или расплывчатое, множество А универсального множества Х характеризуется функцией принадлежности mА: Х ® [0,1], которая ставит в соответствие каждому элементу число mА(х) из отрезка [0,1], указывающее степень принадлежности элемента х нечёткому множеству А. Функция принадлежности mА(х) задаётся числом. Обычное множество является частным случаем нечётких множеств. Для них mА(х) = 1, если хÎ А, и mА(х) = 0, если х Ï А. Обычно если А – конечное нечёткое подмножество Х, то А записывается в виде: А = m1/х1 + m2/х2 + … + mn/хn. (3.1) Например, если Х – множество русских писателей, а подмножество А – «великий русский писатель». Вес писателей различен, поэтому отнести их к «великим» можно с различным весом: А = 1/Толстой + 1/Достоевский + … + 0,8/Короленко + 0,7/Лесков + … + 0,2/… Всех писателей спроектировали от 0 до 1. Знак «+» условен и не имеет отношения к математическому суммированию. Произвольное непрерывное размытое подмножество А из Х представляется так: А = Например, если Х = {1,2,3,4,5}, то нечёткое множество А может быть задано как А = 0,3/1 + 0,4/2 + 0,6/3 + 0,7/4 + 0,8/5. Часто вероятность проектируется на интервал от 0 до 1, поэтому иногда значения весовой функции рассматриваются как вероятности. Функция mА(х) в свою очередь является нечётким понятием, так как зависит от субъективного мнения человека и каждый может давать своё размытое множество. Одна из задач принятия решений – это получение функций принадлежности m для конкретных случаев. Это осуществляется, например, экспертами. Носителем нечёткого множества называется множество таких точек базового множества Х, для которых величина mА(х) ≥ 0. Высотой нечёткого множества называется понятие поверхности функции принадлежности sup mА(x). Нормальным нечётким множеством называется нечёткое множество, для которого sup mА(x) = 1. 3.2. Операции с нечеткими множествами Над нечёткими множествами могут совершаться определённые операции. Рассмотрим некоторые свойства нечётких множеств
1. Эквивалентность. Нечёткое множество является эквивалентным, когда для любых элементов этих множеств имеет место соотношение: mА(x) = mB(x), (3.3) то есть функции принадлежности равны для любого элемента. 2. Включение. Нечёткое множество А содержится в нечётком множестве В тогда, когда для всех элементов базового множества Х имеет место соотношение: mА(x) Í mB(x). (3.4) Например, если Х – все русские писатели, В – множество писателей, А – множество прогрессивных писателей. 3. Алгебраическая сумма. Эта операция с нечёткими множествами обозначается А m А и эквивалентна вероятности суммы двух совместных событий. Например: Х = {a,b,c,d,e} – базовое множество, при этом: А = 0,1/a + 0,2/b + 0,5/c + 0,6/d + 1/e, B = 0,5/b + 0,6/c + 0,3/d. В этом случае алгебраическая сумма А 4. Дополнение. Если А – размытое множество, тогда функция принадлежности множества Применительно к рассмотренному примеру: А = 0,9/a + 0,8/b + 0,5/c + 0,4/d. 5. Объединение. Если А и В – нечёткие множества, то при операции объединения A m А где Ú - поиск максимума из двух. Например, из предшествующего примера: А 6. Пересечение. Если А и В – нечёткие множества, то функция принадлежности их пересечения А m А где Ù – минимум из двух. Например: А 7. Произведение. Если А и В – нечёткие множества, то функция принадлежности их произведения А × В имеет вид: m А × В (х) = mА(х)×mВ(х). (3.9) Например: А × В = 0,1/b + 0,3/c + 0,18/d. 8. Возведение в степень. Если А – нечёткое множество и возводится в положительную степень a > 0, Aa, то это приводит к растяжению нечёткого множества, если это дробная степень A1/2,то концентрация, обозначаемая как Aa = con(A).
Например, можно увидеть на рисунке:
mА(х)
mраст mcon х 2) Х = {1,2,3, …,10}; “Число примерно 5”: A = 0,8/3 + 1/5 +0,6/6; “Число примерно 4”: B = 0,3/3 + 1/ 4 + 0,5/6 A = 1/1 +1/2 + 0,2/3 + 1/ 4 + 0,4/6 + 1/7 + 1/8 + 1/9 + 1/10 AÚB = 0,8/3 + 1/ 4 + 1/5 + 0,6/6 AÙB = 0,3/3 + 0,5/6 A×B = 0,56/3 +0,3/6 9. Комбинация нечётких множеств. Если А1,А2, …, Аn – являются нечёткими подмножествами универсального множества Х, а w1,w2, …,wn - являются неотрицательными весовыми коэффициентами, для которых выполняется условие: mA(X) = w1/m1 + w2/m2 + … + wn/mn. (3.10) 10. Декартово произведение. Если А1,А2, …, Аn – нечёткие подмножества универсальных множеств Х1,Х2, …,Хn, тогда декартовым произведением размытых множеств называется нечёткое множество А1 х А2 х … х Аn заданное на декартовом произведении базовых множеств Х1 х Х2 х … х Хn и имеют функцию принадлежности: mA = m1(x1) Ù m2(x2) Ù … Ù mn(xn). Например: Х1 = Х2 = {3,5,7} А1 = 0,5/3 + 1/5 + 0,7/7; А2 = 1/3 + 0,6/5, тогда: А = А1 х А2 = 0,5/(3,3) + 1/(5,3) + 0,7/(7,3) + 0,5/(3,5) + 0,6/(5,5) + 0,6/(7,5) 3.3. Нечёткие отношения На основе декартова произведения в рассмотрение вводится понятие нечёткого отношения. n -арное нечёткое отношение R в Х1 ´ Х2 ´ … ´ Х n является нечётким подмножеством. Особую роль при построении математической модели нечётких систем играют нечёткие бинарные отношения. Нечётким бинарным отношением R называется нечёткое подмножество множества Х ´ Х, характеризуемое функцией принадлежности: mR(xi, xj) = mRi j для всех < xi, xj > Î Х ´ Х и принимающее значение от 0 до 1. Для решения практических задач нечёткие бинарные отношения удобно задавать в виде матрицы. Допустим, элементы множества Х представлены в виде последовательности: Х = {х1, х2, х3, х4}.Тогда матрицу нечёткого бинарного отношения: R = 0,1/(x1 x2) + 0,1/(x1 x2) + 0,5/(x2 x3) + 0,2/(x3 x2) + 0,7/(x4 x1) можно представить в виде матрицы:
0,1 0,1 0 0 x1 R = 0 0 0,5 0 x2 0 0,2 0 0 x3 0,7 0 0 0 x4 Пересечением нечётких бинарных отношений R и Q называется нечёткое бинарное отношение R m R где Ù– минимальное отношение. Пример:
Если [R] = 0,7 1 0; [Q] = 0 0,6 0,9, 0,2 0 0,4 0,1 0,5 0
0 0,3 0 [R 0,1 0 0 Объединением нечётких отношений R и Q называется отношение R m R
1 0,5 0 [R 0,2 0,5 0,4 Дополнением нечёткого отношения R называется отношение m
[ 0,8 1 0,6 Обратным отношением к отношению R называется R–1 с функцией принадлежности: m R–1 (xi xj) = mR (xj xi), (3.15) т.е. матрица R–1 является трансендентом по отношению к матрице R. Для примера:
[R–1] = 0,3 1 0. 0 0 0,4 Для практического применения аппарата теории нечётких множеств важным является принцип обобщения (рассмотрения). С его помощью можно понятие функции переносить на размытое множество. Допустим: · f – отображение X на Y, т.е. y = f(x), где x и y – производные элементы из X и Y; · А – нечёткое подмножество х, заданное в виде: А = m1/х1 + m2/х2 + … + mn/хn (3.16) или в общем виде: А = В соответствии с принципом обобщения интеграла образ А после действия функции f задаётся: f(А) = m1/f(х1) + m2/f(х2) + … + mn/f(хn ) (3.18) или в непрерывном случае: f(А) = где f(x) – точка множества Y; mА(х) задаёт степень принадлежности f(х) нечёткому подмножеству f(А) множества Y, поэтому образ множества А при отображении f можно получить зная образы элементов х1, х2, …,хn при отображении. В случае, когда имеется функция n-переменных, т.е.: f = X1 ´ X2 ´ X3 ´…´ Xn ® Y, и нечёткое множество А, X1 ´ X2 ´ X3 ´…´ Xn определяется функцией принадлежности mА(х1, х2, …,хn), где хi Î Хi. Принцип обобщения можно представить в следующем виде: f(А) = f [ Если известно не само множество А, а только проекции А1,А2,..., Аn на Х1,Х2, …,Хn, то функция принадлежности:
mA (х1 … xn) = (mA1/(х1) Ù mA2/(х2) Ù … Ù mAn/(хn)). (3.21) Из полученных соотношений следует, что принцип обобщения даёт возможность осуществить отображение нечётких множеств из одного пространства в другое. Например: Х1 = Х2 = {1,2,3,…,10}. На базовых множествах заданы нечёткие множества: А1 ~ 2 = 0,6/1 + 1/ 2 + 0,8/3; А2 ~ 6 = 0,8/5 + 1/6 + 0,7/7. Функциональная зависимость задана: f(X1, X2) = X1 × X2 – арифметическое произведение базовых множеств. Требуется найти функцию f(A1, A2) нечётких множеств: f(A1,A2) = 2*6 = (0,6/1 + 1/ 2 + 0,8/3)*(0,8/5 + 1/6 + 0,7/7) = = 0,6/5 + 0,8/10 + 0,8/15 + 0,6/6 + 1/12 + 0,8/8 + 0,6/7 + 0,7/21 = 12. 3.4. Нечёткая переменная Более сложным понятием в теории принятия решений является переменная, включающая в себя нечёткие множества. Задаётся нечёткая переменная тремя параметрами: [ X, U, R (x)], где Х – название переменной; U – базовое множество; R(x) – нечёткие множества подмножества, представляющие собой нечёткое ограничение и обусловленны названием переменной. Например, скорость самолёта представляется в виде следующего графика: U – базовое множество от 0 до ¥;
1
СУ 0,8
ТУ 0,3
ПО-2 0,1 U, км / ч 0 200 900 2000 Каждому нечёткому названию присваивается число из Х = U: R(x) – уравнение назначения на нечёткую переменную. Ту степень, с которой удовлетворяется это равенство, называют совместимостью U с R(x). Фактически она определяется функцией принадлежности mR(x) (U). Пример: mR(x) (200) = 0,1. Главная проблема – получить mR(x), так как она является субъективной величиной, обычно определяемой методом экспертных оценок. 4. Анализ информационно-управляющих систем 4.1. Общие методические указания Итак, вы приступаете к освоению практических задач формулировки и системного анализа информационно-управляющих систем. Перед вами ставится главная цель - научиться принимать наилучшие (оптимальные) решения в сложных ситуациях со многими противоречивыми требованиями и при существующих ограничениях. Для этого от вас требуются: - внимательность; - самостоятельность (не стоит узнавать, что делает сосед по столу, и копировать его); - творчество (сочиняя обстановку и условия операции, не скупитесь на фантазию). Прежде чем приступить к выполнению первого задания, вы должны мысленно выбрать себе роль руководителя любого ранга (мастера, начальника цеха, директора, научного руководителя, организующего сложный научный эксперимент, военного командира и т.д.), принимающего решение по управлению любой системой, в которой циркулируют потоки управляющей информации. Выбирая объект исследования и разрабатывая управляющую информацию, необходимо иметь в виду, что при этом должна быть заложена возможность различной организации процесса управления, разных вариантов решения. От организации операции управления зависит достигаемый ею эффект, поскольку целью обычно выбирается максимизация конечного результата или минимизация связанных с ним расходов. При этом в условиях управления (как и всегда в реальной жизни) существуют ограничения, мешающие прямому достижению максимальной эффективности, без каких-нибудь уступок.
Не упускайте из виду, что цель управления, ограничения на операцию и оптимальное решение должны будут в итоге выполнения упражнений выражены в математической формулировке. Это в дальнейшем, а сейчас…
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.62.45 (0.076 с.) |
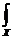 mА(х)/х. (3.2)
mА(х)/х. (3.2) В. Для неё функция принадлежности:
В. Для неё функция принадлежности: :
: m
m 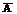 (x) = 1 - mА(х). (3.6)
(x) = 1 - mА(х). (3.6)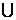 B функции принадлежности:
B функции принадлежности: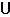 В(х) = max (mА(х)×mВ(х)) = mА(х) Ú mВ(х), (3.7)
В(х) = max (mА(х)×mВ(х)) = mА(х) Ú mВ(х), (3.7)  В минимальна:
В минимальна: В(х) = min [mА(х)×mВ(х)] = mА(х) Ù mВ(х), (3.8)
В(х) = min [mА(х)×mВ(х)] = mА(х) Ù mВ(х), (3.8) 1)
1)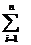 wi = 1, то выпуклая комбинация нечёткого множества образует нечёткое множество А с функцией принадлежности:
wi = 1, то выпуклая комбинация нечёткого множества образует нечёткое множество А с функцией принадлежности:
 х1 х2 х3 х4
х1 х2 х3 х4 Q = (xi xj) = mR (xi xj) Ù mQ (xi xj), (3.12)
Q = (xi xj) = mR (xi xj) Ù mQ (xi xj), (3.12)

 1 0,3 0 0 0,5 0
1 0,3 0 0 0,5 0 
 то матрица пересечений будет иметь вид:
то матрица пересечений будет иметь вид:  Q = (xi xj) = mR (xi xj) Ú mQ (xi xj). (3.13)
Q = (xi xj) = mR (xi xj) Ú mQ (xi xj). (3.13)
 с функцией принадлежности типа:
с функцией принадлежности типа: (xi xj) = 1 - mR (xi xj). (3.14)
(xi xj) = 1 - mR (xi xj). (3.14) Для отношения R из ранее рассмотренного примера имеем:
Для отношения R из ранее рассмотренного примера имеем: 0 0,7 1
0 0,7 1  ] = 0,3 0 1.
] = 0,3 0 1.
 1 0,7 0,2
1 0,7 0,2  mА(х)/х. (3.17)
mА(х)/х. (3.17)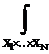 mA (х1 … xn) / (х1 … xn)] =
mA (х1 … xn) / (х1 … xn)] =  mA (х1 … xn) / f(x1 … хn). (3.20)
mA (х1 … xn) / f(x1 … хn). (3.20) R(x) задаёт ограничение на интервале непрерывного базового множества.
R(x) задаёт ограничение на интервале непрерывного базового множества.


