
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение и сумма подпространств.
Определение. Пусть 1) 2) Теорема 3. Пересечение и сумма подпространств являются подпространствами. Доказательство. 1) Если
2) Если В таком случае Если
Теорема 4. О размерности суммы подпространств. Пусть Доказательство. Пусть Выберем базис
Аналогично, все векторы
Есть 3 системы:
Докажем, что система 1) Докажем, что она ЛНС. Предположим, что она ЛЗС, т.е.
где вектор
Тогда 2) Докажем, что любой вектор Вектор Вектор
Итак, (3) ЛНС и через неё выражается любой вектор, значит, это базис. Вспомним, что количество векторов в нём
- - - Перерыв - - - Определение прямой суммы. Сумма подпространств Обозначение:
Теорема 5. (о прямой сумме подпространств). Сумма Доказательство. Необходимость. Пусть сумма является прямой суммой, но
Пусть Достаточность. Пусть
Теорема 6. Сумма подпространств является прямой суммой тогда и только тогда, когда Доказательство. Необходимость. По теореме 4,
Достаточность. Так как
Пример. Всякое векторное пространство является прямой суммой своих подпространств, равных линейным оболочкам Упражнение. Сколько векторов содержит линейное пространство векторов-строк длины n над полем Если каждая координата имеет вид Например, над полем
Линейная зависимость над конечным полем. Коллинеарные векторы Однако, здесь образуют ЛЗС и векторы
При этом определитель:
Рассмотрим векторы
В этом случае для линейной комбинации строк матрицы, где одна строка матрицы умножается на Пример прямой суммы не векторных подпространств. Упражнение. Доказать, что
Рассмотрим матрицы 1) Матрица 2) Матрица При этом Например,
Лекция 13. 21.12.2020.
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 876; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.247.31 (0.021 с.) |
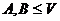 .
.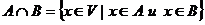 называется пересечением подпространств
называется пересечением подпространств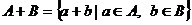 называется суммой подпространств.
называется суммой подпространств.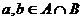 , то одновременно
, то одновременно 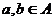 ,
, 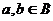 . Так как
. Так как 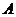 подпространство, то
подпространство, то 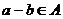 ,
, 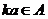 . При этом
. При этом 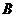 тоже подпространство, так что
тоже подпространство, так что 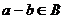 ,
, 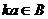 . Таким образом,
. Таким образом,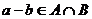 ,
, 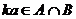 , а значит, по критерию подпространства,
, а значит, по критерию подпространства,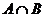 подпространство.
подпространство.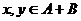 , то каждый из этих элементов представляется в виде:
, то каждый из этих элементов представляется в виде: 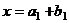 ,
, 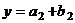 , где
, где 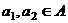 ,
, 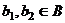 .
. 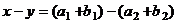 =
= 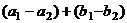 , каждое из
, каждое из 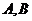 подпространство, значит,
подпространство, значит, 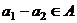 ,
, 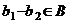 , то есть
, то есть 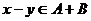 .
.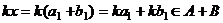 .
. 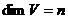 ,
, 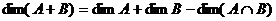 .
. 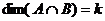 ,
, 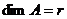 ,
, 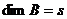 .
.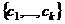 пространства
пространства 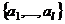 ,что система
,что система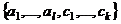 является базисом в
является базисом в 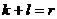 .
. 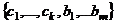 . Но так как размерность
. Но так как размерность 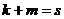 .
. 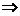
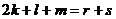
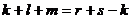 .
. 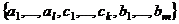 (3) возможно, базис в
(3) возможно, базис в  . (докажем).
. (докажем).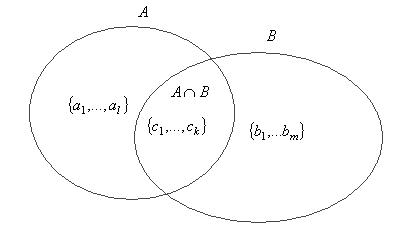
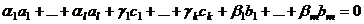 ,
, 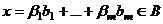 . Но тогда он равен
. Но тогда он равен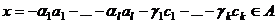 . Значит, этот вектор принадлежит пересечению
. Значит, этот вектор принадлежит пересечению 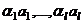 , т.е.
, т.е. 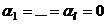 .
.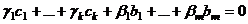 . Но система
. Но система 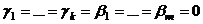 , т.е. вообще все эти коэффициенты 0. То есть, эта система ЛНС.
, т.е. вообще все эти коэффициенты 0. То есть, эта система ЛНС.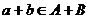 , где
, где 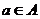 ,
, 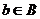 линейно выражается через эту систему (3).
линейно выражается через эту систему (3).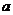 линейно выражается через (1), при этом (1) входит в (3), значит,
линейно выражается через (1), при этом (1) входит в (3), значит, 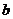 линейно выражается через (2), при этом (2) входит в (3), значит,
линейно выражается через (2), при этом (2) входит в (3), значит, 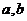 выражаются через (3), значит,
выражаются через (3), значит,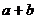 выражается через (3).
выражается через (3).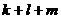 и равно
и равно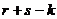 =
= 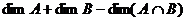 .
. 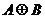 .
.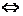
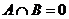 .
. 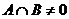 . Тогда некоторый ненулевой вектор
. Тогда некоторый ненулевой вектор 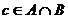 .
.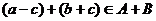 , где первая компонента
, где первая компонента 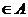 , вторая
, вторая 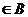 . Действительно, ведь
. Действительно, ведь 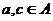 ,
, 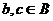 , поэтому
, поэтому 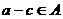 ,
, 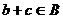 .
. 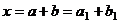 , где
, где 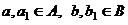 . Но тогда вектор
. Но тогда вектор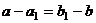 принадлежит
принадлежит 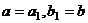 и представление единственно.
и представление единственно. 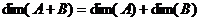 .
. 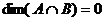 , и
, и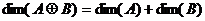 .
. означало бы
означало бы 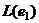 ,...,
,..., 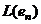 .
.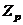 ? (p простое число).
? (p простое число).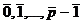 . Если
. Если 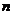 координат, то общее число векторов
координат, то общее число векторов 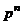 .
. 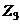 ,
, 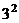 .
. 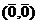 ,
, 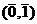 ,
, 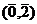
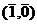 ,
, 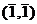 ,
, 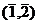
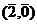 ,
, 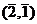 ,
, 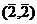
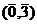 =
= 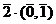 .
. 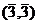 =
= 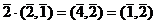
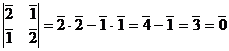 .
. ,
,  . Их линейная комбинация
. Их линейная комбинация 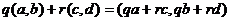 , где
, где 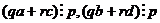 .
. 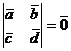 .
.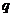 , другая на
, другая на 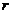 , все координаты делятся на
, все координаты делятся на 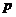 , т.е. вектор
, т.е. вектор 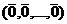 . Строки ЛЗ, определитель 0.
. Строки ЛЗ, определитель 0.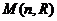 – линейное пространство всех матриц порядка n над полем
– линейное пространство всех матриц порядка n над полем 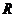 , является прямой суммой двух подпространств:
, является прямой суммой двух подпространств: 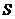 всех симметрических матриц и
всех симметрических матриц и 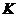 – всех кососимметрических матриц.
– всех кососимметрических матриц. 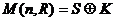 .
. 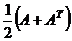 и
и 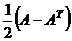 .
. 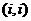 останутся
останутся 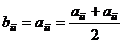 , на прочих местах:
, на прочих местах: 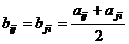 .
. 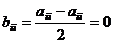 ,
, 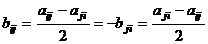 .
. 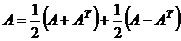 =
= 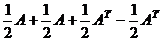 .
. 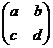 =
= 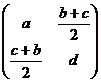 +
+ 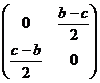 .
. 


