
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 20. Комплексные числа , действия над комплексными числами.
Понятие комплексного числа возникло в первую очередь в результате потребностей автоматизации вычислений. Даже простейшие алгебраические операции над действительными числами выводят за пределы области действительных чисел. Так, например, решение простейшего уравнения x2 + 1 =0 не может быть разрешено в действительных числах, так как x = Тем самым, нужно или отказаться от автоматического применения установленных методов решения и каждый раз проводить подробное исследование возможности их применения, или расширить область действительных чисел, с тем чтобы основные алгебраические операции всегда были выполнимы. Таким расширением действительных чисел являются комплексные числа.
Алгебраическая форма комплексного числ a Определение. Комплексным числом называется двучлен вида 74 где x и y – действительные числа; x = Re z называется действительной частью комплексного числа; y = Im z - мнимая часть комплексного числа. Определение. Два комплексных числа называются равными, когда равны их действительные и мнимые части. Если z1 = x1 + iy1 и z2 = x2 +iy2 , то при z1=z2 Определение. Комплексное число Сумма комплексных чисел есть комплексное число: z = z1 Произведение комплексных чисел есть комплексное число: z1 Отношение
Тригонометрическая форма комплексного числа Каждому комплексному числу z = x + i y поставим в соответствие точку с координатами (x, y) на плоскости R2. Это соответствие взаимно однозначное и называется геометрической интерпретацией комплексного числа. y Множество точек z образует комп - л лксную плоскость, которую будем обоз-
z3 z2 начать (z). Точки z – это концы векторов, проведённых из начала координат. z4 z1 Как и вектор, комплексное число можно 0 тора, диуса). r = 2k Рис.1 Комплексная плоскость
Так как то r =
75
Из рис.1 следует, что Запишем таблицу для определения аргумента комплексного числа z.
Для значения z=0 аргумент не определён. Используя формулы (2), запишем: z = x+ iy = r cos - тригонометрическая форма комплексного числа. (3)
Действия над комплексными числами в тригонометрической форме
Даны два комплексных числа z1= r1 (cos
1. Произведение. z1 Arg Если имеется n одинаковых сомножителей z
2). Деление.
Таким образом при делении: 76 3). Извлечение корня n - й степени из комплексного числа. Определение. Корнем n-й степени из комплексного числа z называется такое число Обозначим z = возведём Комплексные числа равны, если равны их модули и аргументы, поэтому
Пример. Вычислить Решение. В формуле (6) z = 1; r = 1. tg k=0, k=1, k = 2,
Показательная форма комплексного числа Любое число z Эта форма комплексного числа получается, если применить формулу Эйлера В показательной форме удобно производить действия: Пример. Записать в показательной форме число z = 1 – Решение. r = 2; tg
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.016 с.) |
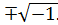
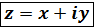 , (1)
, (1)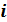 – const, такое, что
– const, такое, что 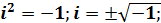
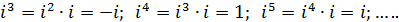
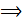 x1 = x2; y1 = y2.
x1 = x2; y1 = y2.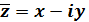 называется сопряжённым комплексному числу z= x+ iy.
называется сопряжённым комплексному числу z= x+ iy.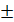 z2 = (x1
z2 = (x1  z2 = (x1 +i y1) (x2 +i y2) = x1 x2 + i x1y2 + ix2y1 – y1y2 = (x1x2 –y1y2)+ i (x1y2 +x2y1).
z2 = (x1 +i y1) (x2 +i y2) = x1 x2 + i x1y2 + ix2y1 – y1y2 = (x1x2 –y1y2)+ i (x1y2 +x2y1). комплексных чиселесть комплексное число:
комплексных чиселесть комплексное число:  =
= 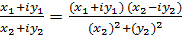 =
= 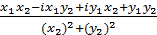
 .
.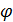 x определить с помощью угла и длины век-
x определить с помощью угла и длины век-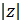 ,
, 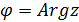 с точностью до
с точностью до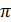 , k = 0,
, k = 0, 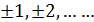
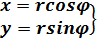 , (2)
, (2)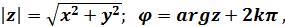
 где
где 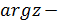 главное значение аргумента z, удовлетворяющее условиям -
главное значение аргумента z, удовлетворяющее условиям - 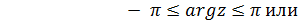 0
0 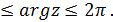
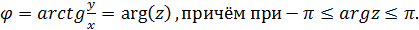
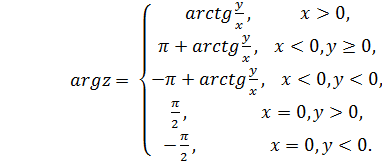
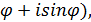
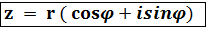 -
-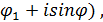
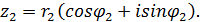
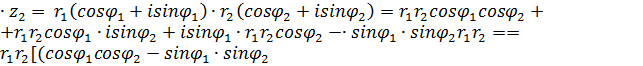 ) + i(cos
) + i(cos 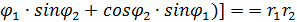 [ cos(
[ cos(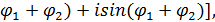 т.е. при умножении
т.е. при умножении 
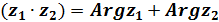
 …….
…….  ,то [r (cos
,то [r (cos 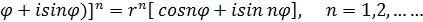
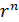 (cos
(cos 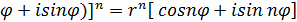 , окончательно:
, окончательно: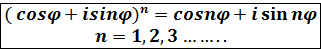 - формула Муавра. ( 4)
- формула Муавра. ( 4)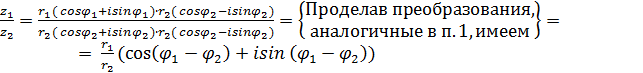 .
.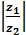 =
= 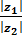 ; Arg
; Arg 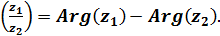
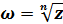 , что
, что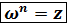 . (5)
. (5)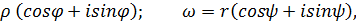
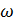 в n-ю степень по формуле Муавра.
в n-ю степень по формуле Муавра.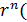
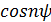
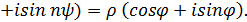
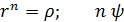 =
= 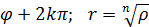 ;
; 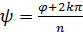 ;
;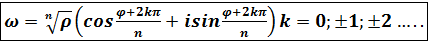 (6)
(6)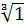 ;
;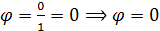 n=3.
n=3.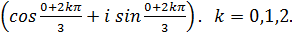
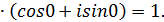
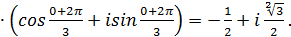
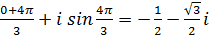 .
.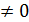 можно записать в показательной форме
можно записать в показательной форме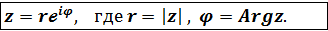 (7)
(7)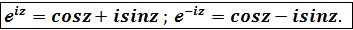 (8)
(8)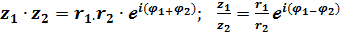
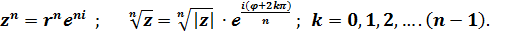
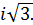
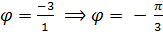 , подставляем в формулу (7) z = 2
, подставляем в формулу (7) z = 2 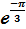 .
.


