
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одно свойство логарифма и предела функции.
Если существует Пример 1. Пользуясь вторым классическим пределом, вычислить: Решение. Пример 2. Вычислить:
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции Пусть
1. Функции Пример. Сравнить функции: Решение. Вывод. Функции
2. Функция Пример. Сравнить функции Решение. Вывод. Функция
3. Функция
4. Функции Пример. Пусть Решение. Вывод. Функции
5. Две функции Пример. Вычислить Вывод. arcsinx Можно показать, что arctg x Составим таблицу эквивалентных функций: при x
Теорема. Предел отношения 2-х б.м. функций равен пределу отношения эквивалентных им функций. Доказательство. Пусть
1 Замечание.Под знаком предела можно заменять функции им эквивалентными. Примеры. Вычислить:
Сравнение бесконечно больших функций Пусть f(x) и 1. Если 2. Если f(x) = 0[
70
Лекция 19. Непрерывность функции. Последовательности
Непрерывность функции
Пусть функция y= f(x) определена при некотором значении x0 и y0 = f(x0). Если x получит приращение Определение 1. Функция y= f(x) называется непрерывной в точке x = x0, если она определена в этой точке и если Пример. Показать, что функция y = Решение. Область определения этой функции вся числовая ось. Составим приращение функции Вывод. Функция y = Определение 2. Пусть функция y= f(x) непрерывна в точке x0, тогда В последнем равенстве обозначим x0 +
1. f (x) – определена в точке x 0 и в некоторой её окрестности. 2. f (x) имеет предел при x = x 0, это значит, что она имеет предел слева, справа и они равны между собой, и равны значению функции в точке x = x 0.
Если в какой либо точке x0 одно из условий не выполняется, функция называется разрывной в этой точке, точка x0 называется точкой разрыва. Определение. 1. Точкой разрыва 1-го рода функции y=f(x) называется такая точка x0 в кото- рой функция имеет левый и правый пределы неравные между собой. 2. Точкой разрыва 2-го рода или бесконечного разрыва называется точка x0 в которой хотя бы один из пределов не существует или равен Пример 1. Установить характер точки разрыва функции y = Решение. В точке x=0 функция не существует, то есть 71 ки разрыва, найдём пределы слева и справа.
y
0 x
Пример 2. Установить характер точек разрыва для функции y= Решение. В окрестности точки x=3 функция меняет своё значение, поэтому в этой точке может быть разрыв. Проверим это, найдём все пределы.
Ответ. Так как предел слева не равен пределу справа, то x=3 точка разрыва 1-го рода. y 9- - - - - - 7-- - - - - 0 3 x
Теорема 1. Если функции Теорема 2. Сложная функция y = f [ Пример. Y = sin (x3 + 4x – 2); y =
Свойства непрерывных функций на отрезке 1. Если функция f(x) непрерывна на отрезке [ Y
0
72 2. Если функция f(x) непрерывна на [ 3. Если функция f(x) непрерывна на [ y
0
4. Если функция f(x) непрерывна на [ A C B
0 Последовательности Определение. Упорядоченное множество чисел, каждое из которых имеет свой номер называется последовательностью. Обозначается: { xn } = x0 , x1, x2,…..xn …, где xn - общий член последовательности. Пример. { xn } = { Определение. Дискретной прерывной переменной называется переменная, которая принимает отдельные оторванные друг от друга значения, { xn }.
Предел последовательности Определение. Число А называется пределом последовательности {xn }, если Раскроем последнее неравенство
A-
73 Определение. По другому определение предела: Определение. Число А называется пределом последовательности { Вычисляются пределы дискретной переменной точно так же как и для непрерывной переменной. Пример 1. Вычислить Пример 2. Вычислить Определение. Последовательность называется сходящейся, если она имеет предел. Определение. Последовательность y1 ,y2, y3 ….yn называется ограниченной, если существует такое число С, что Теорема. Всякие ограниченные последовательности имеют предел и обратно. Пример. Дана последовательность 1, Решение. Как видно - это бесконечно убывающая геометрическая последовательность, можно найти её сумму S =
|
|||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.36.141 (0.071 с.) |
 , то
, то 
 x+3.
x+3.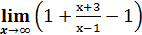 x +3 =
x +3 = 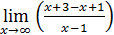 x+3=
x+3= 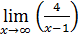 x+3=
x+3=  =
=  =
=  Ответ:
Ответ: 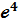

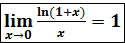
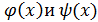 – это значит, найти предел их отношения при x
– это значит, найти предел их отношения при x 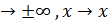 0.
0.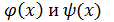 – б.м.функции.
– б.м.функции. называются б. м. одного и того же порядка малости, если
называются б. м. одного и того же порядка малости, если 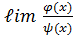 = c =const
= c =const 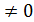 .
.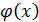 = x2-4 и
= x2-4 и 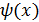 = x2-5x +6при x
= x2-5x +6при x 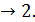


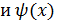 одного и того же порядка малости.
одного и того же порядка малости.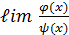 = 0.
= 0. и
и  .
.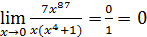 .
.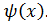
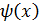 если
если .
.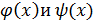 называются не сравнимыми,если
называются не сравнимыми,если 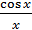 ,
, 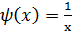 , x
, x  .
. =
= 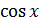 , не сущуствует.
, не сущуствует.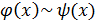
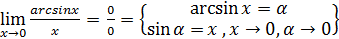 =
= 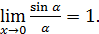
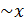

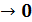
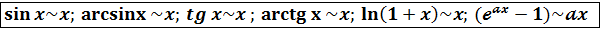
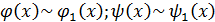 . Докажем, что
. Докажем, что 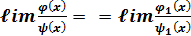 . Имеем
. Имеем 

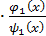

 ]=
]= 


 =
=  ч.т.д. 1
ч.т.д. 1  1/2x =
1/2x = 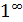 =
=  =
=  .
.
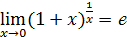 .
.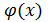 б.б.функции.
б.б.функции.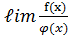 =0, то f(x) имеет низший порядок по сравнению с
=0, то f(x) имеет низший порядок по сравнению с 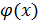 , запись
, запись 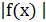
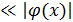 или f(x) = 0[
или f(x) = 0[ 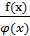 = С, то говорят, что отношение
= С, то говорят, что отношение 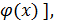 ноль большой.
ноль большой.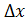 , то и функция y получит приращение
, то и функция y получит приращение  , то есть f(x0 +
, то есть f(x0 + 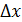 ) = y0 +
) = y0 + 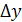
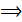

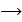 приращение функции.
приращение функции.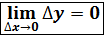 , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
, то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.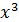 непрерывна в произвольной точке.
непрерывна в произвольной точке.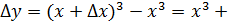
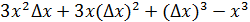 , перейдём к пределу
, перейдём к пределу 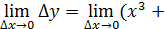
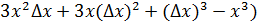 =0
=0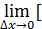 f(x0 +
f(x0 + 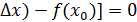 или
или 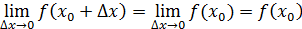
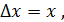 при
при 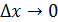 x
x 
 . Окончательно, функция f(x) называется непрерывной в точке x0 , если
. Окончательно, функция f(x) называется непрерывной в точке x0 , если 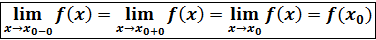
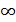 .
. .
.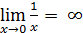 ,значит x=0 точка разрыва 2-го рода. Чтобы изобразить график функции в окрестности точ-
,значит x=0 точка разрыва 2-го рода. Чтобы изобразить график функции в окрестности точ- ;
; 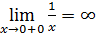 .
. 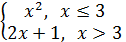
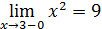 ;
; 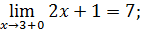
 =9; y(3)=9.
=9; y(3)=9. , то есть
, то есть 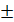

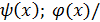
 , образованная из 2-х непрерывных функций f (x) и
, образованная из 2-х непрерывных функций f (x) и 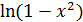
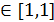 .
.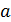 , b ] , то она достигает на этом отрезке (сегменте) своего наибольшего и наименьшего значения
, b ] , то она достигает на этом отрезке (сегменте) своего наибольшего и наименьшего значения , где m – наименьшее, а М наибольшее значения функции на этом отрезке.
, где m – наименьшее, а М наибольшее значения функции на этом отрезке. . Или b,
. Или b, 
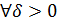 найдётся такой номер N, что, начиная с этого номера выполняется условие
найдётся такой номер N, что, начиная с этого номера выполняется условие  <
< 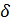 при n
при n 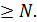 Обозначается
Обозначается 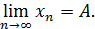
 <
< 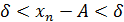
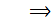 A-
A- 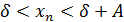 , геометрически
, геометрически n
n 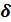 - окрестностью точки
- окрестностью точки 
 , если начиная с некоторого номера N все элементы последовательности оказываются в
, если начиная с некоторого номера N все элементы последовательности оказываются в 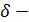 окрестности.
окрестности.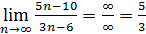
 =
= 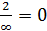 .
. выполняется неравенство
выполняется неравенство 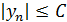 .
. 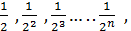 определить сходящаяся она или нет?
определить сходящаяся она или нет?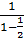 = 2, то есть эта последовательность имеет предел, а это значит она ограничена и сходящаяся.
= 2, то есть эта последовательность имеет предел, а это значит она ограничена и сходящаяся.


