
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 5. Понятие вектора. Основные операции над векторами.
Определение. Пространство, в котором введены декартовы координаты x,y,z, так, что выполняются следующие условия: 1) разным точкам пространства соответствуют разные наборы координат; 2) каждому набору x,y,z соответствует какая – то точка Р, изучаемого пространства; называется 3-х мерным декартовым и обозначается Определение. Геометрическим вектором или просто вектором называется направленный отрезок прямой. Обозначается Определение. Вектором называется матрица размерности (n Длина вектора– это его модуль, абсолютная величина,обозначается Определение. Вектор называется нулевым, если его начало и конец совпадают. Определение. Векторы называются коллинеарными, если они лежат на одной либо на параллельных прямых, их можно всегда представить Определение. Векторы называются компланарными, если они лежат в одной плоскости. Определение. Два вектора называются равными, если 1) коллинеарны, 2) имеют одинаковое направление, 3) имеют равные длины.
20
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Определение. Cуммой
Свойства суммы 1) 2) ( 3) 4) существует такой противоположный вектор Определение. Суммой нескольких векторов называется вектор, который замыкает ломанную линию, составленную из векторов слагаемых.
Правило параллелограмма
Если векторы
Определение. Произведением вектора 1) 21 3) векторы Cвойства произведения на число 1) 2) ( 3) Пример. Построить вектор Решение. 3
Проекция вектора на ось
Определение. Ортогональной проекцией вектора B A k A’ B’
Теорема. Проекция вектора Доказательство теоремы следует из рисунка.
Основные свойства проекций
1) п 2) п 3) п Вывод. Линейные операции над векторами сводятся к точно таким же операциям над их проекциями.
22 Понятие линейной зависимости векторов Определение. Линейной комбинацией n векторов где Определение. Векторы Определение. Векторы Теорема 1. Необходимым и достаточным условием линейной зависимости 2-х векторов является их коллинеарность. Доказательство необходимости. Пусть 2 вектора По определению линейной зависимости векторов найдутся такие
Последнее равенство означает, что векторы коллинеарны ч.т.д. Доказательство достаточности. Пусть Теорема 2. Необходимым и достаточным условием линейной зависимости 3-х векторов является их компланарность. Теорема 3. Любые 4-е вектора в
Понятие базиса. Аффинные координаты Определение. 3 линейно независимые вектора Это разложение вектора в базисе Определение. Числа Определение. Базис Теорема 1. Всякий вектор Доказательство. Пусть и ещё есть разложение Вычтем из (1) (2) 0 = Определение. Три некомпланарных вектора O
Определение. Вектор
Декартова система координат (д.с.к.) Определение. Аффинный базис { O, В силу теоремы о разложении вектора в базисе для д.с.к. X,Y,Z – координаты вектора, Теорема. Декартовы прямоугольные координаты X,Y,Z вектора Доказательство. Сделаем рисунок Z M k o j i по построению. x 24
Определение. Проекции вектора Теорема Пример. Найти координаты вектора Решение. По теореме Ответ.
Определение. Радиус вектор – это вектор, соединяющий начало координат и точку А, обозначается
|
||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.54.63 (0.08 с.) |
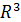 ;
;  – двумерное декартово пространство – плоскость;
– двумерное декартово пространство – плоскость; 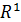 - одномерное декартово пространство – прямая. Координаты – (от латинского слова) упорядоченный, определённый.
- одномерное декартово пространство – прямая. Координаты – (от латинского слова) упорядоченный, определённый.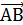 , А – начало, В – конец вектора или
, А – начало, В – конец вектора или 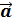 или
или 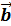 .
. или (1
или (1 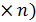 ;
; 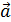 = (n
= (n 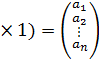 ,
, 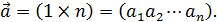
 ,
, 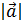 .
.
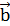
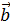
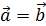
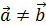
 2-х векторов называют вектор, идущий из начала первого в конец второго, при условии, что
2-х векторов называют вектор, идущий из начала первого в конец второго, при условии, что 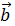 выходит из конца
выходит из конца 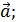
 ) +
) + 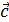 =
= 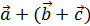 ;
; =
= 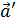 , что
, что 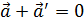 .
.
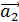
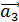
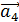
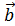 приложены к общему началу и на них построен параллелограмм, то
приложены к общему началу и на них построен параллелограмм, то 
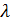 называется вектор
называется вектор 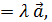 удовлетворяющий условиям:
удовлетворяющий условиям:
 и противоположны, если
и противоположны, если 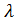 =0, то
=0, то 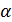 (
( ;
;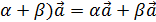 ;
;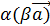 =
= 
 =2
=2 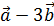 .
. =
= 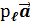
 А’ B’
А’ B’ 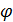


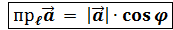 .
.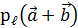
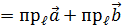 ;
; п
п 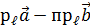 ;
;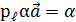 п
п 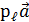 ;
;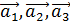 …..
….. 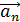 называют сумму произведений этих векторов на произвольные вещественные числа, то есть выражение вида:
называют сумму произведений этих векторов на произвольные вещественные числа, то есть выражение вида: , (1)
, (1) 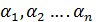 - числа.
- числа.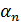 , из которых хотя бы одно не равно нулю, что линейная комбинация (1) обращается в ноль
, из которых хотя бы одно не равно нулю, что линейная комбинация (1) обращается в ноль 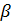 , что
, что  +
+  =0, пусть
=0, пусть 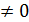 ,тогда разделим на
,тогда разделим на 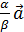 +
+ 
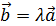 или
или 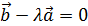 это значит зависимы,ч.т.д.
это значит зависимы,ч.т.д. образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор 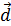 может быть представлен в виде некоторой линейной комбинации векторов
может быть представлен в виде некоторой линейной комбинации векторов 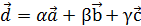 . (1)
. (1)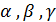 называются координатами вектора
называются координатами вектора 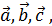 то есть координаты вектора это коэффициенты линейной зависимости, выражающие данный вектор через данный базис.
то есть координаты вектора это коэффициенты линейной зависимости, выражающие данный вектор через данный базис. (1)
(1) (2)
(2)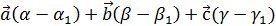 , так как
, так как  - базис, то эта линейная комбинация выполняется тогда, когда
- базис, то эта линейная комбинация выполняется тогда, когда 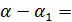
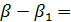
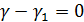 отсюда
отсюда 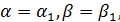
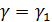 , то есть разложения совпадают ч.т.д.
, то есть разложения совпадают ч.т.д.
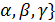
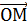 , соединяющий начало и точку М, называется радиусом вектором точки М.
, соединяющий начало и точку М, называется радиусом вектором точки М.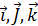 }.
}.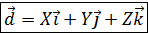
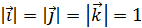 – орты.
– орты.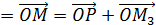

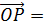
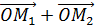
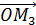
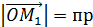 xOM;
xOM; y OM;
y OM;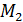 y
y  z OM;
z OM; P
P  ;
; 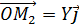 ;
; 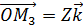 , так как коллинеарны.
, так как коллинеарны.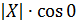 °
°  =
= 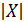 ;
; 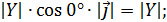
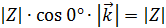 ч. т. д.
ч. т. д. Линейные операции над векторами сводятся к точно таким же линейным операциям над их одноимёнными координатами.
Линейные операции над векторами сводятся к точно таким же линейным операциям над их одноимёнными координатами.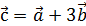 , если
, если  ;
; 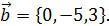
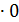 =1; yc =2+3
=1; yc =2+3 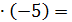 -13; zc = 3+3
-13; zc = 3+3 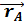 = { X, Y, Z}.
= { X, Y, Z}. 


