
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 2 . Понятие матрицы. Основные операции над матрицами. Собственные числа и собственные векторы матрицы.Стр 1 из 10Следующая ⇒
Определение. Матрицей называется прямоугольная таблица из m строк и n столбцов элементов некоторого множества. m
A =
Коротко А = ( Если m = n, то матрица называется квадратной, если m ≠ n, то матрица прямоугольная. Определение. Определитель, составленный из элементов квадратной матрицы называется определителем матрицы. Если матрица A =
Если 8
A =
Порядок матрицы обозначается так: m
ОСНОВНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Определение. Две матрицы A и B называются равными (A = B), если они имеют одинаковое число строк и столбцов и их соответствующие элементы совпадают.
1). Суммой 2-х матриц A = Если A =
C ВОЙСТВА СЛОЖЕНИЯ
а). А + В = В + А. б). (А+ В) +С = А + (В + С).
2). Умножение матрицы на число. Определение. Произведением матрицы А = С =
А =
СВОЙСТВА ПРОИЗВЕДЕНИЯ НА ЧИСЛО а). 9 б). в). ( г). 0 д). С = А-В это С = А + (-1)В.
3). Умножение матриц. А = Определение. Произведением матрицы А = имеющая порядок m
Вывод. Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В и получается матрица, у которой, столько строк сколько их имеет матрица - множимое и столько столбцов, сколько их имеет матрица - множитель. Пример. Перемножить матрицы. Решение.
СВОЙСТВА ПРОИЗВЕДЕНИЯ
а). А∙В ≠ В ∙ А. б). А (ВС) = (АВ)С. в). (А + В)С = АС + ВС.
ОБРАТНАЯ МАТРИЦА.
Определение. Матрица, у которой строки заменены столбцами, называется транспонированной по отношению к первой матрице.
А = 10 Определение. Матрица Определение. Обратной матрицей
Элементами обратной матрицы являются алгебраические дополнения элементов присоединённой матрицы
Изэтой формулы следует, что обратную матрицу имеет только невырожденная матрица. Пример. Найти обратную матрицу для матрицы A = Решение. Вычислим сначала определитель матрицы А.
Чтобы проверить вычисления, найдём А
А
Собственные числа и собственные векторы матрицы
11 Определение. Характеристическим уравнением матрицы А = называется уравнение Корни этого уравнения Определение. Система уравнений в которой
Пример. Дана матрица Решение. Составляем характеристическое уравнение 1). Аналогично. 2).
Лекция. 3 Матричная запись и матричное решение систем уравнений 1-го порядка. Ранг матрицы. Пусть дана система алгебраических уравнений
Коротко эту систему можно записать в тензорном виде: 12 Обозначим:
A =
тогда
A∙X =
Такая запись (3) системы называется матричной формой. A Обе части равенства (4) умножим слева на обратную матрицу
Пример. Матричным методом решить систему: Решение. Решение будем находить в виде X =
А Матрица
13
X =
Ответ:
ПОНЯТИЕ О РАНГЕ МАТРИЦЫ
Пусть имеем матрицу из m строк и n столбцов Например:
А =
Определение. Рангом матрицы называется наибольший из порядков отличных от нуля её миноров. Обозначается: rang A = 3 или Если ранг матрицы А равен r, то это означает, что в матрице А имеется хотя бы один отличный от нуля минор порядка r, но всякий минор порядка Пример. Найти rang матрицы. A =
Делаем вывод, что Этот метод нахождения ранга матрицы достаточно трудоёмкий, так как 14 приходится вычислять много определителей.
ДРУГОЙ МЕТОД НАХОЖДЕНИЯ РАНГА МАТРИЦЫ
Определение. Элементарными называются следующие преобразования: 1). Умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля. 2). Прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число. 3). Перемена местами строк (столбцов) матрицы. 4). Отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю. Матрицы, получаемые одна из другой при элементарных преобразованиях, называются эквивалентными. Эквивалентные матрицы не равны друг другу, но ранги их равны. Теорема. Ранг матрицы не изменяется при элементарных преобразованиях. Пример. Вычислить ранг матрицы А. A =
15 Вывод. Ранг матрицы равен числу единиц, стоящих по диагонали матрицы, если все остальные элементы нули.
Лекция 4. Общая теория решения систем линейных уравнений.
Рассмотрим систему m линейных уравнений с n неизвестными
Определение. Система (1) называется совместной, если она имеет решение и несовместной, если она не имеет решений. Определение. Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой, если она имеет бесчисленное множество решений. Определение. Две совместные системы уравнений называются равносильными, если каждое решение первой системы является решением второй и обратно.
Теорема Кронекера - Капелли. Кронекер (1823-1891)- немецкий математик. Капелли (1855-1910)-итальянский математик. Для того, чтобы система линейных уравнений (1) была совместна, необходимо и достаточно, чтобы ранг матрицы системы
B = 1). Если r(A) = r(B) = n – числу неизвестных, то система (1) имеет единственное решение. 2). Если же r(A) = r(B) < n, то система (1) имеет бесчисленное множество решений, зависящих от (n – r) параметров (свободных неизвестных).
МЕТОД ГАУССА (Метод последовательных исключений)
Этот метод продемонстрируем на примере, так как он запрограммирован на электронных машинах и хорошо там просчитывается. Пример. Решить систему уравнений методом Гаусса. 16 Установим совместность системы, найдём ранг матрицы, составленной из коэффициентов при неизвестных
В = Решение. Из 1-го уравнения выражаем
Ответ:
ФОРМУЛЫ КРАМЕРА
ЗАДАЧА. Решить систему 2-х линейных уравнений с 2-мя неизвестными. Решение. Умножим обе части первого уравнения на
17
Пример. Решить систему уравнений: Решение.
Из формул Крамера следует: 1). 2). 3).
18 ЛИНЕЙНЫЕ ОДНОРОДНЫЕ СИСТЕМЫ
Определение. Система m уравнений с n неизвестными вида:
называется линейной однородной системой. Следуя формулам Крамера, можно сделать вывод: 1). 2). Теорема. Для того, чтобы система (1) имела ненулевое решение необходимо и достаточно, чтобы её определитель Доказательство необходимости. Пусть система (1) имеет ненулевое решение, но По формулам Крамера имеем:
Доказательство достаточности. Пусть Возьмём r(A) < n и по теореме Кронекера – Капелли система (1) имеет бесчисленное множество решений в том числе и ненулевое. Вывод. Однородная система уравнений всегда совместна и имеет ненулевое решение только тогда, когда определитель системы равен нулю Пример. Решить систему уравнений.
Ранг матрицы последней системы равен 2-м, а число неизвестных равно 3-м, поэтому, следуя теореме Кронекера – Капелли, 3-2=1 =-27z-z=-28z. X = Ответ. X = 5z; Y = -7z, где z любое число.
19 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.90 (0.159 с.) |
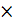 n - порядок матрицы. Если m=n, то матрица называется квадратной, m
n - порядок матрицы. Если m=n, то матрица называется квадратной, m  n – прямоугольной. Обозначается:
n – прямоугольной. Обозначается: или A =
или A = 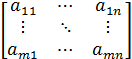 , или A =
, или A = 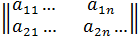
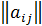 (i =
(i = 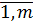 j =
j = 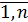 ), числа
), числа 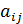 - элементы матрицы.
- элементы матрицы.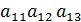 ) - матрица строка;
) - матрица строка; 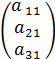 - матрица столбец.
- матрица столбец.
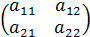 , то определитель
, то определитель 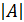 =
= 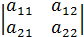
 – нуль матрица. E =
– нуль матрица. E =  - единичная диагональная матрица.
- единичная диагональная матрица.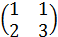 =
= 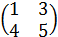 ≠
≠  ; (1 2 3) ≠
; (1 2 3) ≠ 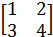 .
.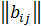 (i =
(i = 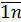 ) называется матрица C =
) называется матрица C = 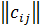 , (i =
, (i = 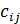 =
= 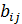 ,т.е. С=A+B.
,т.е. С=A+B.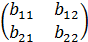 , то С =
, то С = 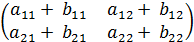 или
или  +
+ 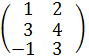 =
= 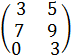
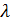 называется матрица С =
называется матрица С =  (i=
(i= 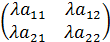 .
. А =
А = 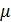 А).
А).  А = 0
А = 0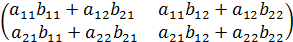
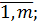 j =
j =  ) называется матрица С =
) называется матрица С =  ),
),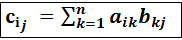 i = 1,2,
i = 1,2,  m; j = 1,2,
m; j = 1,2, 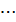 p. С = А ∙ В (1)
p. С = А ∙ В (1)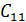 =
= 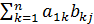 =
= 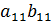 +
+ 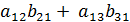
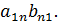

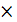
 =
= 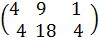
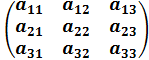
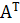 =
= 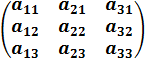
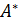 , составленная из алгебраических дополнений к элементам матрицы
, составленная из алгебраических дополнений к элементам матрицы 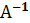 к квадратной матрице А называется матрица, удовлетворяющая условию
к квадратной матрице А называется матрица, удовлетворяющая условию
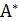 , делённые на число, равное определителю матрицы А, т. е. det A =
, делённые на число, равное определителю матрицы А, т. е. det A = 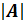
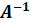 =
=  =
= 
 .
.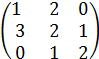
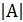 = 4+0+0 – 0 -1 – 12 = - 9, определитель матрицы не равен нулю, поэтому матрица А имеет обратную. Находим алгебраические дополнения.
= 4+0+0 – 0 -1 – 12 = - 9, определитель матрицы не равен нулю, поэтому матрица А имеет обратную. Находим алгебраические дополнения.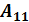 = 3
= 3  = - 4
= - 4 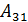 = 2
= 2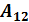 =-6
=-6 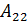 = 2
= 2 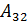 = - 1
= - 1 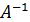 =
= 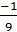
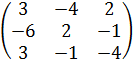 .
. = 3
= 3 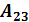 = - 1
= - 1 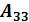 = -4
= -4 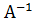 .
. =
= 
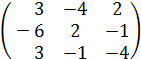 =
=  = Е.
= Е.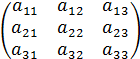
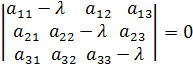
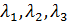 называются характеристическими числами матрицы.
называются характеристическими числами матрицы.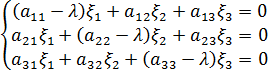
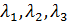 (и определитель которой в силу этого равен 0) определяет тройку чисел (
(и определитель которой в силу этого равен 0) определяет тройку чисел (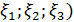 , соответствующую данному характеристическому числу, эта совокупность трёх чисел определяет вектор
, соответствующую данному характеристическому числу, эта совокупность трёх чисел определяет вектор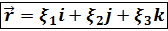 , называемый собственным вектором матрицы
, называемый собственным вектором матрицы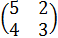 , найти её характеристические числа и собственные векторы.
, найти её характеристические числа и собственные векторы.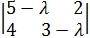 = 0
= 0 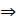
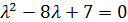
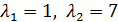 .
.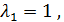 подставляем в систему
подставляем в систему 
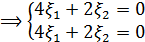 эта система имеет бесчисленное множество решений, полагаем
эта система имеет бесчисленное множество решений, полагаем 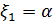 , тогда
, тогда 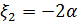 и собственный вектор
и собственный вектор  .
.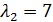 ,
, 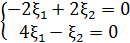
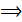
 ,
, 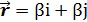 .
.
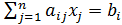 , i = 1
, i = 1 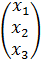 ; B =
; B =  ,
, =
= 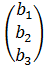 . (3)
. (3) операторная форма (4)
операторная форма (4)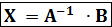 -матричное решение системы (1).
-матричное решение системы (1). 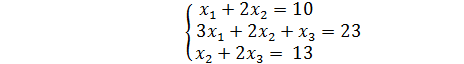
 , для этого найдём обратную матрицу для матрицы А, составленную из коэффициентов при неизвестных
, для этого найдём обратную матрицу для матрицы А, составленную из коэффициентов при неизвестных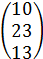 .
.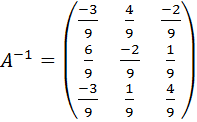 =
= 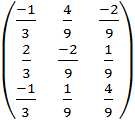
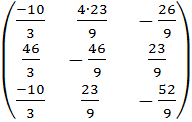 =
= 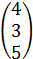
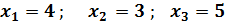 .
. Определение. Минором k-го порядка матрицы А называется определитель квадратной матрицы, получающийся из данной матрицы выделением произвольных k строк и k столбцов.
Определение. Минором k-го порядка матрицы А называется определитель квадратной матрицы, получающийся из данной матрицы выделением произвольных k строк и k столбцов.
 - минор 3-го порядка.
- минор 3-го порядка.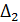 =
= 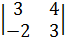 - минор 2-го порядка.
- минор 2-го порядка.
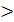 чем r равен нулю.
чем r равен нулю.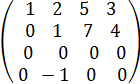 . Начинаем искать миноры не равные нулю с наибольшего порядка.
. Начинаем искать миноры не равные нулю с наибольшего порядка. 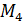 =
=  ;
; 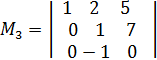 = 7
= 7 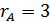 , так как минор 3-го порядка отличен от нуля.
, так как минор 3-го порядка отличен от нуля.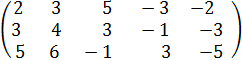
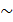
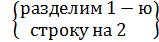

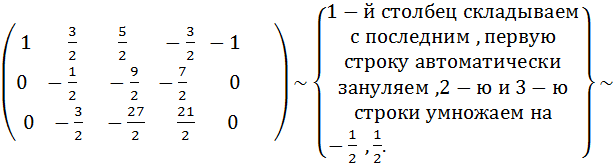



 , rang(A) = 2.
, rang(A) = 2.
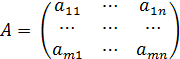 был равен рангу её расширенной матрицы
был равен рангу её расширенной матрицы , полученную путём добавления к основной матрице А столбца из свободных членов системы.
, полученную путём добавления к основной матрице А столбца из свободных членов системы.
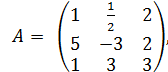 det A =
det A = 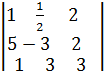 =-9+1+30+6-6-
=-9+1+30+6-6- 
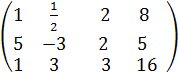 , так как в ней содержится det A
, так как в ней содержится det A 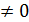 , то rang B также равен 3. Делаем вывод: согласно теореме Кронекера-Капелли r(A)=r(B)=3-числу неизвестных, поэтому система совместна и имеет единственное решение.
, то rang B также равен 3. Делаем вывод: согласно теореме Кронекера-Капелли r(A)=r(B)=3-числу неизвестных, поэтому система совместна и имеет единственное решение. 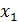 и подставляем во 2-е и 3-е
и подставляем во 2-е и 3-е 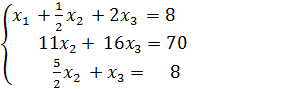 Из 2-го уравнения выражаем
Из 2-го уравнения выражаем 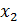 и подставляем в 3-е.
и подставляем в 3-е.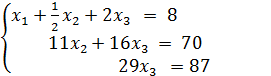 Теперь обратным ходом из 3-го выражаем
Теперь обратным ходом из 3-го выражаем 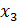 и подставляем во 2-е уравнение, из 2-го выражаем
и подставляем во 2-е уравнение, из 2-го выражаем 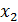 и подставляем 1-е, окончательно получаем:
и подставляем 1-е, окончательно получаем: 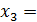 3;
3;  1.
1.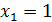 ;
;  ;
; 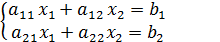
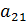 , а 2-го на
, а 2-го на 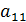 и вычтем из 1-го уравнения 2-е.
и вычтем из 1-го уравнения 2-е.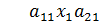 +
+ 
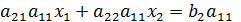
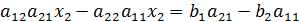
 . Числитель этой дроби равен определителю –
. Числитель этой дроби равен определителю –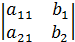 . Знаменатель равен -
. Знаменатель равен -  =
= 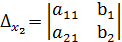 , тогда
, тогда 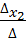 . Аналогичными действиями можно получить
. Аналогичными действиями можно получить  , где
, где 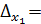
 . Решение системы запишем в виде:
. Решение системы запишем в виде: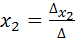 . Для системы, состоящей из трёх уравнений с тремя неизвестными эти формулы примут вид:
. Для системы, состоящей из трёх уравнений с тремя неизвестными эти формулы примут вид: , это и есть формулы Крамера, где
, это и есть формулы Крамера, где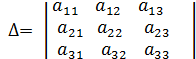 ,
, 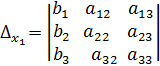 ,
, 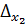 =
= 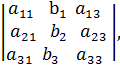
 .
. 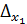 ,
, 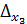 - побочные.
- побочные.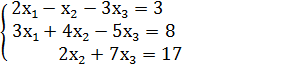
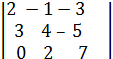 = 79
= 79 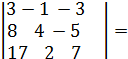 =395,
=395, 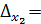
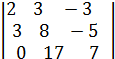 =-158,
=-158,  = 237.
= 237.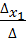 = 5;
= 5; 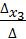 . Ответ.
. Ответ. 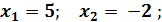
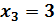 .
.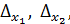
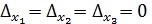 , то система имеет бесчисленное множество решений или совсем не имеет решения.
, то система имеет бесчисленное множество решений или совсем не имеет решения.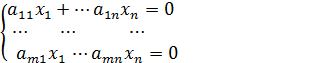 (1)
(1) система имеет единственное нулевое решение.
система имеет единственное нулевое решение.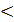 n
n 
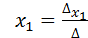 ,
, 
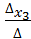

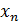 =
=  , так как есть ненулевое решение, предположим, что это
, так как есть ненулевое решение, предположим, что это 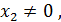 то
то 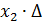 =
= 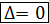 .
.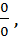
 ,
,  .
.
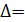
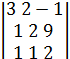 = 0. →
= 0. → 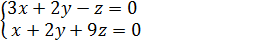
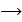 свободное неизвестное. Систему перепишем так:
свободное неизвестное. Систему перепишем так: 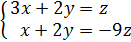 и решаем её по формулам Крамера. Для этого найдём
и решаем её по формулам Крамера. Для этого найдём  ,
, 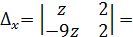 2z+18z=20z,
2z+18z=20z,  =
= =
= 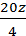 = 5z; Y =
= 5z; Y = 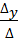 =
=  .
.


