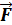Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Длина вектора. Направляющие косинусы.
Пусть вектор Рассмотрим вектор z A B k так как x i j y Обозначим углы наклона вектора Определение. Косинусы углов, образованных между вектором и осями координат, называются направляющими косинусами вектора z x o y
Возведём в квадрат обе части равенств (1) и сложим, получим 25 co
Условия коллинеарности двух векторов
Пусть вектор Правило. Если векторы коллинеарны, то их координаты пропорциональны. Определение. Единичный вектор, направленный по вектору
Пример. Найти орт вектора Решение. Найдём модуль вектора
Деление отрезка в данном отношении
Определение. Разделить отрезок Пусть даны точки Z М1 М M2 x o y x – x1 = z – z1 = Если точка М середина отрезка, то М1 М = М М2 и Xcp. = Если 26
ЛЕКЦИЯ 7. Скалярное произведение векторов. Векторное произведение.
Определение. Скалярным произведением векторов Обозначается (
Физический смысл скалярного произведения
Из физики известно, что работа силы по перемещению, находится по формуле А = F S Если
Свойства скалярного произведения
1. ( 2. 3. ( 4.Если 5. ( 6. ( 7. ( Выражение скалярного произведения через координаты перемножаемых векторов Пусть вектор 27 лярные произведения базисных векторов равны нулю, так как они взаимно перпендикулярны } =
Запишем основные формулы в декартовых координатах: п Пример. Найти работу силы Решение. А = (
Векторное произведение векторов Правые и левые тройки векторов Определение. Тройка векторов
Левая Правая Определение. Аффинная система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку. Определение. Векторным произведением вектора 1). 2). Вектор
Обозначается
Свойства векторного произведения
1. [ 2. 28 4. Если 5.Модуль векторного произведения равен площади параллелограмма, построенного на векторах сомножителях.
Физический смысл векторного произведения
1). Рассмотрим физическую задачу. Пусть твёрдое тело вращается с угловой скоростью М – произвольная точка, z направленная по касательной к окружности,
описываемой точкой М. ddD OO1M
x Вывод: векторное произведение угловой скорос - ти на радиус – вектор произвольной точки вращающегося тела есть линейная скорость.
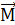 силы силы 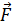 , приложенной к точке В тела есть векторное произведение вектора –плеча на вектор-силы. , приложенной к точке В тела есть векторное произведение вектора –плеча на вектор-силы.
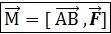
B
|
||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.198 (0.052 с.) |
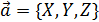 , так как он является диагональю параллелограмма, то по теореме из школы
, так как он является диагональю параллелограмма, то по теореме из школы 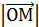 2 =
2 = 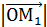 2 =
2 = 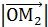 2 =
2 = 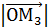 2 или
2 или 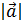 2 = X2 +Y2 +Z2 отсюда
2 = X2 +Y2 +Z2 отсюда (1)
(1) 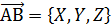 ; точки А(
; точки А(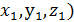 и В (
и В (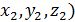

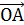 ;
; 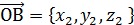 ;
; 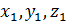 },
}, 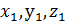 и
и 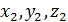 - проекции , то
- проекции , то 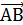 = {
= { 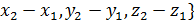 , a модуль вектора
, a модуль вектора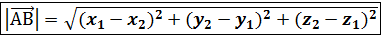
 c осями координат ox,oy,oz соответственно
c осями координат ox,oy,oz соответственно  .
.
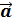 Если вектор
Если вектор 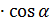 ;
; 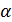
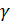
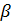 y=
y= 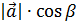 ; z =
; z = 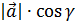 , как проекции,отсюда
, как проекции,отсюда 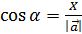 ,
, 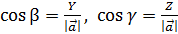 или
или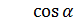 =
= 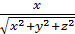 ;
; 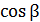 =
= 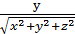 ;
; 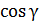 =
=  (1)
(1) 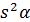 + co
+ co 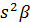 +co
+co 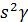 =
= 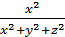 +
+ 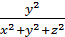 +
+ 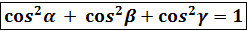
 условие того, что
условие того, что 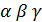 углы вектора с осями координат.
углы вектора с осями координат.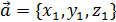 коллинеарен вектору
коллинеарен вектору  , тогда
, тогда 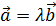 по теореме (
по теореме (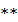 ) имеем
) имеем 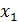 =
= 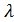
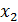 ,
, 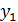 =
= 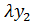 ,
, 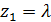
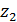 из этих равенств находим
из этих равенств находим 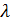 , то есть
, то есть 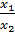
 ;
; 
 =
= 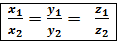
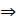 условие коллинеарности векторов.
условие коллинеарности векторов. 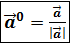
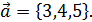
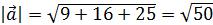 , тогда орт вектора запишется
, тогда орт вектора запишется  = {
= { 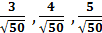 }.
}. в данном отношении
в данном отношении  это значит найти на данном отрезке такую точку М, что имеет место равенство
это значит найти на данном отрезке такую точку М, что имеет место равенство 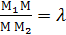 или М1М
или М1М 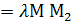 .
.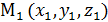 и
и 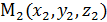 , найдём координаты точки М (x, y, z), делящей отрезок
, найдём координаты точки М (x, y, z), делящей отрезок 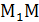 2 в отношении
2 в отношении 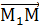 = { x - x1, y – y1, z – z1 };
= { x - x1, y – y1, z – z1 }; 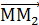 = { x2 – x, y2 – y, z2 – z }.
= { x2 – x, y2 – y, z2 – z }.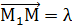
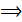 x (1+
x (1+  x =
x = 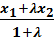 y – y1 =
y – y1 = 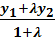
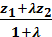
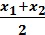 , Ycp. =
, Ycp. = 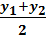 , Z cp. =
, Z cp. = 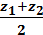 .
.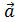 и
и 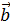 называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними. =
= 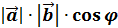

 S
S  F
F 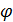
 вектор перемещения, то работа А =
вектор перемещения, то работа А = 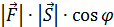 = = (
= = (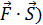 , то есть работа равна скалярному произведению векторов силы и пути
, то есть работа равна скалярному произведению векторов силы и пути

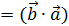 следует из определения;
следует из определения;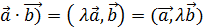 ;
;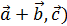 = (
= (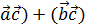 ;
;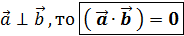 , так как
, так как  ;
;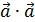

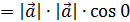 0
0 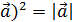 2 или
2 или 
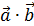
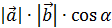
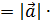

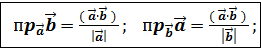

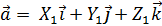 а вектор
а вектор 
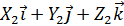 , найдём их скалярное произведение (
, найдём их скалярное произведение (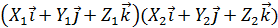 =
= 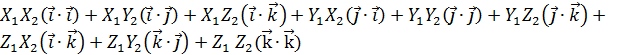 = { (
= { ( =
= 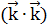 =1, другие ска-
=1, другие ска-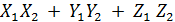 .
.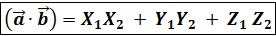
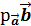 =
= 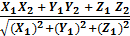 ;
; 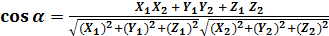 ;
;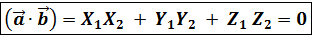 → условие перпендикулярности 2-х векторов.
→ условие перпендикулярности 2-х векторов.  по перемещению в направлении вектора
по перемещению в направлении вектора 
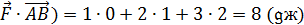 .
.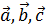 называется правой (левой), если после приведения к одному началу, вектор
называется правой (левой), если после приведения к одному началу, вектор  располагается по ту сторону плоскости, определяемой векторами
располагается по ту сторону плоскости, определяемой векторами 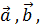 откуда поворот от
откуда поворот от 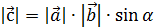 ;
;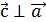 и
и  3). Вектор
3). Вектор 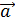 и
и 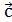
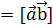 или
или 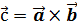 .
.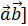
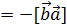 антикоммутативно;
антикоммутативно;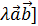 = [
= [ 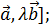 3. [
3. [ 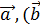 +
+ 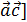 ;
;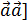
 , так как
, так как 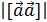 =
= 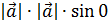 = 0;
= 0; =
= 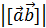
 S =
S = 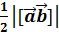 .
. 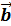
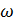 вокруг неподвижной оси.
вокруг неподвижной оси. 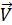 - линейная скорость,
- линейная скорость, 

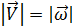
 ,
, 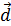 ⊥ оси oz, из треугольника
⊥ оси oz, из треугольника , тогда
, тогда 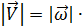
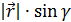
 так как
так как 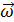 и
и 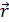 , а поворот от
, а поворот от 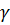
 y сматривать как векторное произведение, то есть
y сматривать как векторное произведение, то есть