
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектр квадратної матриці другого порядку ⇐ ПредыдущаяСтр 7 из 7
Множина усіх власних значень квадратної матриці другого порядку називається її спектром. Якщо така множина є двоелементною, то кажуть, що матриця має простий спектр. Теорема. Квадратна матриця А другого порядку з простим спектром подібна до діагональної. Доведення. Оскільки така матриця А є подібною до жорданової матриці, то вона подібна до матриці виду Суперечність. Теорему доведено.
3.9. Рівняння
І. Розглянемо спочатку рівняння 1). 1). Нехай Отже, Отже, Перевірка показує, що О і справді є розв’язком рівняння. 2). Нехай Нехай Т - довільна неособлива матриця, тоді Справді, Таким чином, множина всіх розв’язків рівняння Зауваження. Якщо задано деяке матричне рівняння ІІ. Розв’яжемо тепер рівняння
Нехай
Отже, Далі, нехай Отже, всі розв’язки рівняння
де Т – довільна неособлива матриця.
1. Знайти спектр матриці 2. Розв’язати матричне рівняння порядку. 3. Звести до жорданової форми матрицю 4. Розв’язати матричне рівняння порядку, де 5. Розв’язати матричне рівняння порядку.
6. Розв’язати матричне рівняння порядку
Список літератури
1. Скорняков Л.А. Элементы алгебры. – Москва. – Наука. – 1980. – 240 с. 2. Мальцев А.И. Основы линейной алгебры. – Москва.– Наука. – 1970. – 400 с. 3. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. – Москва. – МГУ. – 1980. – 320 с. 4. Ланкастер П. Теория матриц. – Москва. – Наука. – 1978. – 280 с. 5. Горбачук О.Л., Воробець Б.Д. Вступ до вищої алгебри. – Львів. – ЛДУ. –1976. – 88 с.
|
|||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.154.185 (0.013 с.) |
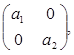 або до матриці виду
або до матриці виду 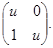 Припустимо, що вона подібна до матриці
Припустимо, що вона подібна до матриці 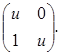 Тоді ці матриці мають однакові характеристичні рівняння, а, отже, і множини їх коренів. Проте множина коренів рівняння
Тоді ці матриці мають однакові характеристичні рівняння, а, отже, і множини їх коренів. Проте множина коренів рівняння 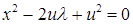 є одноелементна. Отже, матриця А має два однакових власних значення.
є одноелементна. Отже, матриця А має два однакових власних значення.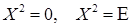
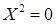 , в якому
, в якому 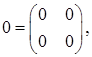 а Х - невідома квадратна матриця другого порядку. Нехай Х 0- якийсь розв’язок цього рівняння. Тоді існує (згідно попередніх пунктів) матриця Т, для якої
а Х - невідома квадратна матриця другого порядку. Нехай Х 0- якийсь розв’язок цього рівняння. Тоді існує (згідно попередніх пунктів) матриця Т, для якої 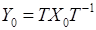 - жорданова матриця. Y 0 - теж розв’язок цього рівняння. Справді,
- жорданова матриця. Y 0 - теж розв’язок цього рівняння. Справді, 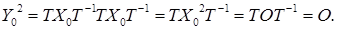 Оскільки Y 0 - жорданова матриця, то можливі наступні варіанти її вигляду:
Оскільки Y 0 - жорданова матриця, то можливі наступні варіанти її вигляду: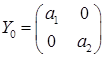 або 2).
або 2). 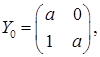 де а 1, а 2, а - числа (комплексні).
де а 1, а 2, а - числа (комплексні).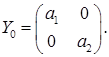 Тоді
Тоді 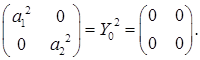 Тому
Тому 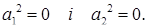
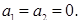 Тоді
Тоді 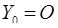 .
.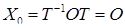 .
.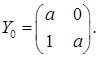 Тоді
Тоді 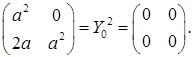 Тому
Тому 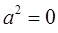 . Отже,
. Отже, 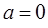 . Тоді
. Тоді 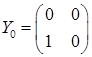 . Отже,
. Отже, 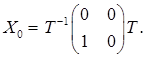
 - розв’язок рівняння.
- розв’язок рівняння.
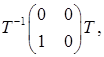 де Т – довільна неособлива матриця, і з
де Т – довільна неособлива матриця, і з 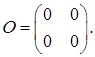
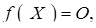 яке має наступну властивість: якщо Х 0 - розв’язок, а Т - довільна неособлива матриця, то
яке має наступну властивість: якщо Х 0 - розв’язок, а Т - довільна неособлива матриця, то 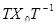 – теж розв’язок, то для його розв’язання, зрозуміло, достатньо знайти розв’язок S в кожному з усіх різних класів подібних матриць (якщо такий розв’язок існує). Всі матриці в класі подібних будуть розв’язками рівняння, якщо хоч один розв’язок з цього класу існує. Представники ж класів подібних матриць краще брати у жордановій формі, оскільки над такими матрицями легше виконувати обчислення і, крім того, такі матриці є єдиними в кожному класі подібних матриць з точністю до порядку слідування жорданових блоків. Прикладами рівнянь з такою властивістю є
– теж розв’язок, то для його розв’язання, зрозуміло, достатньо знайти розв’язок S в кожному з усіх різних класів подібних матриць (якщо такий розв’язок існує). Всі матриці в класі подібних будуть розв’язками рівняння, якщо хоч один розв’язок з цього класу існує. Представники ж класів подібних матриць краще брати у жордановій формі, оскільки над такими матрицями легше виконувати обчислення і, крім того, такі матриці є єдиними в кожному класі подібних матриць з точністю до порядку слідування жорданових блоків. Прикладами рівнянь з такою властивістю є 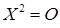 і
і 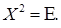
 де
де 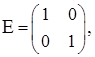 Х - квадратна матриця другого порядку, використавши це зауваження.
Х - квадратна матриця другого порядку, використавши це зауваження. тоді
тоді 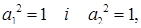 тобто або
тобто або 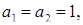 або
або 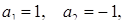 або
або 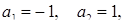 або
або 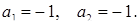 Далі використовуємо п. 3.7. Зрозуміло тоді, що
Далі використовуємо п. 3.7. Зрозуміло тоді, що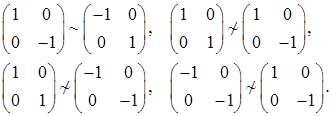
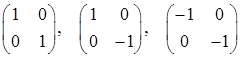 - представники різних класів подібних матриць, які є розв’язками рівняння.
- представники різних класів подібних матриць, які є розв’язками рівняння.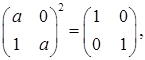 тоді
тоді 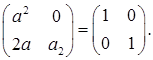 Отже,
Отже, 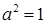 і
і  що неможливо.
що неможливо.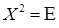 такі:
такі:
 3.10. Вправи
3.10. Вправи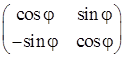 та звести її до діагональної форми.
та звести її до діагональної форми. в квадратних матрицях другого
в квадратних матрицях другого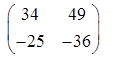
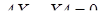 в квадратних матрицях другого
в квадратних матрицях другого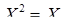 в квадратних матрицях другого
в квадратних матрицях другого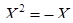 в квадратних матрицях другого
в квадратних матрицях другого



