Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дрогобицький державний педагогічний університетСтр 1 из 7Следующая ⇒
ДРОГОБИЦЬКИЙ ДЕРЖАВНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ ІВАНА ФРАНКА
О.Л.ГОРБАЧУК, Л.І.КОМАРНИЦЬКА, Ю.П.МАТУРІН
МАТРИЦІ ТА СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ НАВЧАЛЬНО-МЕТОДИЧНИЙ ПОСІБНИК Дрогобич - 2007 УДК 512.64(09) К 63 Матриці та системи лінійних рівнянь: Навчально-методичний посібник / Горбачук О.Л., Комарницька Л.І., Матурін Ю.П. – Дрогобич: Редакційно-видавничий відділ ДДПУ, 2007. – 50 с.
Посібник написано відповідно до програми навчальної дисципліни “Лінійна алгебра” для підготовки фахівців освітньо-кваліфікаційного рівня “Бакалавр” спеціальностей “Математика”, “Математика та основи економіки”, “Математика та фізика”, затвердженої Вченою радою Дрогобицького державного педагогічного університету імені Івана Франка. Посібник містить виклад теоретичного матеріалу з даної теми, приклади, що ілюструють теорію та вправи для самостійної роботи. Розрахований на студентів-математиків, які вивчають курс алгебри в педагогічних та класичних університетах, на вчителів математики та старшокласників, які цікавляться математикою.
Бібліографія 5 назв.
Рекомендовано до друку Вченою радою Дрогобицького державного педагогічного університету імені Івана Франка (протокол № 8 від 29 червня 2007 р.)
Відповідальний за випуск: доцент Галь Ю.М. Редактор: Невмержицька Ірина Михайлівна
Рецензенти: Пташник Б.Й., доктор фізико-математичних наук, професор, член-кореспондент НАН України, завідувач відділу математичної фізики Інституту прикладних проблем механіки та математики імені Я.С.Підстригача НАН України; Зарічний М.М., доктор фізико-математичних наук, професор, декан механіко-математичного факультету Львівського національного університету імені Івана Франка.
© Горбачук О.Л., Комарницька Л.І., Матурін Ю.П. ЗМІСТ Вступ ……………………………………………………………………….4 1. Матриці та дії над ними.........................................................................5 1.1. Означення матриць ………………………………………………5 1.2. Види матриць ……………………………………………………..5 1.3. Означення дій над матрицями …………………………………..8 1.4. Властивості додавання матриць та множення матриць на числа …………………………………10
1.5. Символ суми……………………………………………………...11 1.6. Властивості множення матриць ………………………………..12 1.7. Властивості транспонування …………………………………...14 1.8. Обернена матриця у випадку квадратних матриць другого порядку…………………………………………………. 15 1.9. Приклади матриць, елементами яких є вектори……………….18 1.10. Числовий n-вимірний простір………………………………….. 20 1.11. Подібні матриці…………………………………………………. 21 1.12. Вправи…………………………………………………………… 21 2. Системи лінійних рівнянь ……………………………………………23 2.1. Система двох лінійних рівнянь з двома невідомими………… 23 2.2. Системи лінійних рівнянь: основні означення……………… 25 2.3. Елементарні перетворення системи лінійних рівнянь……….. 27 2.4. Східчасті системи……………………………………………… 30 2.5. Зведення системи лінійних рівнянь до східчастого вигляду (Метод Гаусса)………………………………………………….. 33 2.6. Вправи ………………………………………………………….. 36
3. Жорданова форма матриць та матричні рівняння …………37 3.1. Слід квадратної матриці……………………………………….. 37 3.2. Жорданова форма квадратних матриць. Основна теорема…. 38 3.3. Зведення до жорданової форми нижніх трикутних матриць другого порядку…………………………………………………39 3.4. Власні значення і власні вектори квадратної матриці другого порядку………………………………………………………… 41 3.5. Зведення квадратної матриці другого порядку до нижньої трикутної форми…………………………………………………42 3.6. Загальний випадок………………………………………………43 3.7. Однозначність визначення жорданової форми з точністю до порядку слідування діагональних блоків………………………44 3.8. Спектр квадратної матриці другого порядку………………….47 3.9. Рівняння 3.10. Вправи……………………………………………………………49 Список літератури ……………………………………………………. 50 Вступ Метою даного навчального посібника є ознайомлення читача з елементами теорії матриць та систем лінійних рівнянь. Цей матеріал є доступним не лише для студентів-першокурсників, але й для старшокласників.
Серед розглядуваних питань найважливішими є властивості дій над матрицями, рівносильні перетворення систем лінійних рівнянь, жорданова форма матриць та матричні рівняння. Останні питання мають поглибити знання студентів в галузі теорії матриць, користуючись при цьому тільки елементарними засобами. Кожний із розділів закінчується вправами, які ілюструють й доповнюють теоретичний матеріал. Теорія матриць відіграє важливу роль не тільки у всіх галузях математики, але й у фізиці. Тому її вивчення повинно бути дуже ретельним. Матриці з числовими елементами є природнім узагальненням чисел і широко використовуються в алгебрі, як приклади алгебраїчних структур. Так, наприклад, кватерніони Гамільтона можна представляти у вигляді певних квадратних матриць 4-го порядку з дійсними елементами. Якщо ж дозволити елементам матриць пробігати множину елементів певного кільця, то можна отримати приклади нових кілець. Таким способом отримуються кільця із заданими властивостями. Розв’язування систем лінійних рівнянь методом Гаусса фактично зводиться до певних перетворень над їх розширеними матрицями, а тому ця тема є органічним продовженням першого розділу даного посібника. Вивчення теми про жорданову форму матриць дозволить досить просто розв’язувати деякі типи матричних рівнянь. Джерела із списку літератури допоможуть зацікавленим студентам продовжити вивчення тем, викладених у посібнику.
Означення матриць
Матрицею називається прямокутна таблиця, що заповнена певними математичними об’єктами, які називаються елементами матриці. Тут будемо розглядати лише такі матриці, елементами яких є числа. Елементи матриці будемо позначати однією буквою з двома індексами, де перший індекс вказує номер рядка елемента матриці, а другий – номер його стовпця. Таким чином, матриця записується у формі:
Якщо матриця має k рядків і n стовпців, то про таку матрицю кажуть, що вона має розмір k × n. Якщо кількість рядків і кількість стовпців матриці рівні, то така матриця називається квадратною, а кількість її рядків (стовпців) називається її порядком. Матрицю також позначають великими латинськими літерами або за допомогою відповідних малих літер з двома індексами: А = Дві матриці однакових розмірів називають рівними, якщо їх відповідні елементи рівні. Наприклад, матриці A = не є рівними (А ≠ В), оскільки
Види матриць
Матриця, що складається з одного рядка [стовпця], називається матрицею-рядком [ матрицею-стовпцем ]. Матрицю-рядок також називають рядком, а матрицю-стовпець – стовпцем. Використовуються також наступні терміни: вектор-рядок, вектор-стовпець. Вектор, що складається з n елементів, називається n -вимірним. Матриця О довільних розмірів, всі елементи якої дорівнюють нулю, називається нуль-матрицею: О =
Рядок [стовпець], всі елементи якого є нулі, називається нульовим рядком [стовпцем] або нуль-вектором. Одиничною матрицею називається квадратна матриця Е n -го порядку наступного вигляду:
Е =
де Квадратна матриця D називається діагональною, якщо вона має наступний вигляд: D = тобто dij = 0, якщо і ¹ j. Таку матрицю також позначають наступним чином: D = dia g Наприклад, Означення дій над матрицями
Сумою двох матриць однакових розмірів А і В називають матрицю С, кожний елемент якої дорівнює сумі відповідних елементів матриць А і В, тобто С = А + В = (або Добутком матриці А на число λ називають таку матрицю В, кожний елемент якої дорівнює добутку числа λ і відповідного елемента матриці А, тобто: В = λ А = λ (або Матрицю (-1) А позначатимемо через – А і називатимемо її матрицею, протилежною до матриці А. Під різницею матриць А і В (А – В) будемо розуміти суму А + (- В). Зрозуміло, що А – А = О, А + О = О +А = А для всякої матриці А і нуль-матриці О тих же розмірів. Транспонованою до матриці А розмірів k
Транспоновану матрицю позначають через А T, а елементи її через Приклад: А = Для введення добутку двох матриць визначимо спочатку добуток рядка і стовпця однакової довжини (рядок – лівий множник, стовпець – правий множник, бо порядок співмножників тут важливий!):
У результаті одержимо квадратну матрицю першого порядку, яку можна ототожнити з її єдиним елементом Нехай матриця А має розмір Добутком матриць А і В називається матриця С = АВ, що має розмір k c ij = i =1,..., k; j =1,..., r. Приклади: 1). 2). 3). 4).
Нехай А – квадратна матриця n -го порядку, Е – одинична матриця n -го порядку, а О – квадратна нуль-матриця n -го порядку. Тоді легко перевірити, що: АЕ = ЕА = А, АО = ОА = О. Слід зауважити, що добуток двох ненульових матриць може бути нульовою матрицею (нуль-матрицею). Справді, Квадратна матриця В n -го порядку називається оберненою до квадратної матриці А n -го порядку, якщо АВ = ВА = Е. Обернену матрицю до матриці А позначають через Приклад. Нехай А =
1.4. Властивості додавання матриць та множення матриць на числа
Додавання матриць та множення матриць на числа мають наступні властивості:
1. А + (В + С) = (А + В) + С (асоціативність); 2. А + О = О + А = А; 3. А + (- А) = (- А) + А = О; 4. А + В = В + А (комутативність); 5. 6. 7. ( 8. (для довільних матриць А, В, С однакових розмірів і для довільних чисел Доведемо властивості 1 і 7. Всі інші властивості доводяться аналогічно і залишаються для самостійного доведення читачу. 1. А + (В + С) = = = (тут ми використали асоціативність додавання чисел). 7. = (тут ми використали дистрибутивність множення відносно додавання для чисел).
Символи суми Суму 1). Очевидними також є й інші властивості символу суми: 2). 3). де Часто використовуються так звані подвійні суми, які необхідні для підсумовування доданків з двома індексами.
тобто для знаходження суми всіх елементів прямокутної таблиці (матриці):
Тут і, j називаються першим і другим індексами підсумовування відповідно. Очевидно, що сума S всіх елементів даної таблиці дорівнює S = де Тому (Знаходимо суму всіх сум елементів рядків). З другого боку,
(Знаходимо суму всіх сум елементів стовпців). Таким чином, має місце наступна властивість символу подвійної суми: 4). Взагалі кажучи, символ суми може записуватися у найрізноманітніших ситуаціях. Його ж зміст може бути зрозумілим з контексту. Тепер нам легко буде оперувати з матрицями. Наприклад, елемент добутку
Властивості транспонування
1. для довільної матриці А (ідемпотентність); 2. де А і В – довільні матриці однакових розмірів (адитивність); 3. для довільної матриці А і довільного числа λ (однорідність); 4. для довільних матриць А і В, для яких існує добуток АВ; 5. Доведемо ці властивості. 1. Очевидно. 2. Справді, 3. Справді, 4. Нехай U = АВ. Тоді тобто 5. Доведемо першу з рівностей. Використаємо попередню і першу властивості: Матриця А, для якої Таким чином, матриця Приклад:
Вправи 1. Матрицю
2. Нехай 3. Обчислити 4. Коли справджуються рівності 5. Довести, що добуток двох симетричних матриць є симетричною матрицею тоді й тільки тоді, коли ці матриці комутують. 6. Квадратна матриця Довести, що всяку квадратну матрицю можна представити як суму симетричної та кососиметричної. 7. Обчислити 8. Довести: якщо
порядку. 9. Довести формулу 10. Довести, що добуток двох верхніх (нижніх) трикутних матриць однакового розміру є верхньою (нижньої) трикутною матрицею.
Східчасті системи
Східчастою називається така система лінійних рівнянь, матриця якої є східчастою, тобто це система, яка має наступний вигляд:
де або система вигляду тобто система називається східчастою, якщо у розширеній її матриці
Приклади східчастих систем: 1). 2). 3). Системи виду Тому розглянемо системи виду (1). В такій системі невідомі Розглянемо два випадки: І. Нехай серед чисел
де Зрозуміло, що жодна сукупність чисел ІІ. Нехай У відповідності до цього елементи матриці А системи (1) будуть перепозначені на елементи матриці С, тобто система (1) матиме наступний вигляд: де (Рівняння системи (1), починаючи з Надамо вільним невідомим Тоді з попереднього рівняння ( Якщо вже визначені
Так, рухаючись вгору по системі, будуть однозначно визначені Отже, система (2), а тому і система (1) є сумісними, причому при Приклад. Нехай маємо систему
Ця система східчаста і має вигляд (1) (
а тоді можна визначити
тобто Таким чином,
2.5. Зведення системи лінійних рівнянь до східчастого вигляду (метод Гаусса)
В пункті 2.4 було наведено метод розв¢язання східчастих систем (обернений хід методу Гаусса – послідовне знаходження головних невідомих Теорема. Кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень зводиться до системи східчастого вигляду.
Доведення теореми для випадку системи з трьох рівнянь з чотирма невідомими. Спочатку ми доведемо цю теорему для випадку системи, що складається з 3-ох рівнянь і має 4-и невідомі. Справді, нехай маємо систему: Будемо вважати, що матриця даної системи не є нуль-матрицею, бо інакше система вже мала б східчастий вигляд. Тоді серед усіх стовпців матриці А існує ненульовий стовпець Причому можна вважати, що Можливі випадки Якщо матриця
нульова, то система (S2) вже має східчастий вигляд. Розглянемо випадок, коли така матриця Причому можна вважати, що Теорему для даного випадку доведено. Доведення теореми для загального випадку. Доведення проводимо індукцією за числом рівнянь даної системи. 1). Якщо система складається лише з одного рівняння 2). Припустимо, що система з числом рівнянь 3). Покажемо, що тоді і система з числом рівнянь
Справді, нехай маємо систему, що має Якщо матриця даної системи є нуль-матрицею, то система (1) є східчастою. Тому вважатимемо, що матриця системи (1) не є нуль-матрицею. Тоді вона має ненульовий стовпець. Нехай Можна вважати, що Зробимо над системою (2) такі елементарні перетворення (типу В), щоб в усіх рівняннях, починаючи з 2-го, коефіцієнти при
до 3-го рівняння додамо перше, помножене на до Отримаємо таку систему:
Використовуючи до системи з останніх де Тому і вся система (3) зведеться до східчастого вигляду: де Теорему доведено.
Вправи
1. Дослідити систему рівнянь і знайти її розв’язки в залежності від значень параметра
2. Переконатися, що елементарні перетворення
| Поделиться:
| |

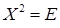 ……………………………………….47
……………………………………….47
 або
або  .
. =
=  , В =
, В =  =
=  .
. , В =
, В = 
 = 8,
= 8,  = 1.
= 1. .
. = [
= [  ij],
ij], – символ Кронекера.
– символ Кронекера.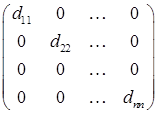 ,
,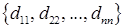 .
. .
.
 для всіх i, j).
для всіх i, j).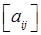 =
= 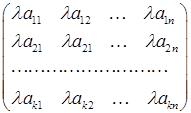 =
= 
 для всіх
для всіх  ).
). n називається така матриця В розмірів n
n називається така матриця В розмірів n  для всіх і, j. Тобто матриця В має за рядки відповідні стовпці матриці А.
для всіх і, j. Тобто матриця В має за рядки відповідні стовпці матриці А. (= а
(= а  ).
).


 =
= 
 Добуток АВ матриць А і В визначаємо тільки тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В.
Добуток АВ матриць А і В визначаємо тільки тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В. , а матриця В – n
, а матриця В – n  .
. дорівнює добутку і -го рядка матриці А і j -го стовпця матриці В:
дорівнює добутку і -го рядка матриці А і j -го стовпця матриці В: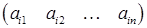
 =
= 

 =
=  ;
;

 ;
;
 =
=  ;
;



 .
. . Тоді В =
. Тоді В =  – обернена матриця до матриці А.
– обернена матриця до матриці А. А = А;
А = А; (А + В) =
(А + В) =  А +
А +  ) А =
) А =  ) А
) А  ,
,  ).
). +
+ 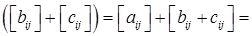

 =
= 



 позначають через
позначають через  , де і називається індексом підсумовування і його позначення ролі не відіграє, тобто його можна замінити будь-якою іншою буквою:
, де і називається індексом підсумовування і його позначення ролі не відіграє, тобто його можна замінити будь-якою іншою буквою: ;
; (адитивність);
(адитивність); (однорідність);
(однорідність);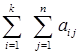











 матриць
матриць  і
і  розмірів
розмірів  і
і  , відповідно, записується наступним чином:
, відповідно, записується наступним чином: .
.
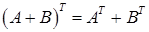 ,
,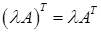
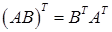
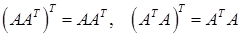 .
.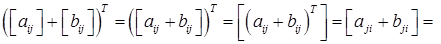
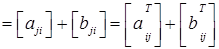 =
= 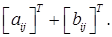
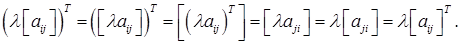
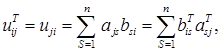
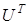 =
= 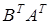 .
.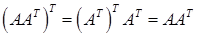 .
.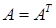 , називається симетричною.
, називається симетричною.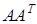 завжди симетрична.
завжди симетрична.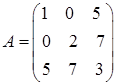 – симетрична матриця.
– симетрична матриця.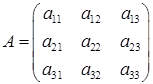 подати, як лінійну комбінацію матриць:
подати, як лінійну комбінацію матриць: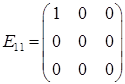 ,
, 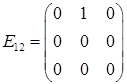 ,
,  ,
, 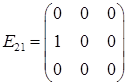 ,
, ,
, 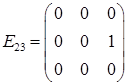 ,
, 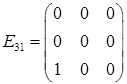 ,
,  ,
,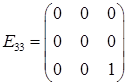 .
.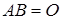 . Чи обов’язково
. Чи обов’язково 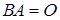 ?
?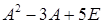 , якщо
, якщо 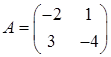 .
.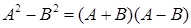 і
і  .
.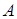 називається кососиметричною, якщо
називається кососиметричною, якщо 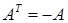 .
.
 , то обидві матриці квадратні та однакового
, то обидві матриці квадратні та однакового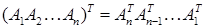 .
.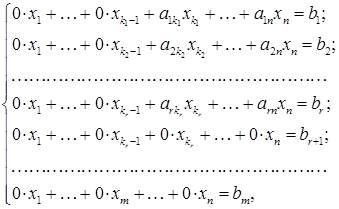 (1)
(1)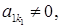
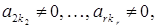
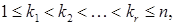


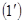
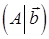 матриця А східчаста.
матриця А східчаста.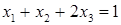 – східчаста система, що складається з одного рівняння (тут
– східчаста система, що складається з одного рівняння (тут 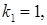
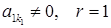 ).
).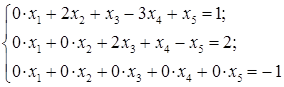 – східчаста система (тут
– східчаста система (тут 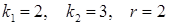 ).
).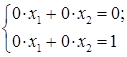 – східчаста система (тут
– східчаста система (тут 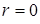 ).
).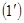 мають множину розв¢язків, що складається з усіх векторів
мають множину розв¢язків, що складається з усіх векторів 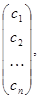 де
де 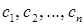 - довільні числа, якщо
- довільні числа, якщо 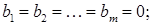 системи виду
системи виду 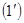 є несумісними, якщо хоч одне з чисел
є несумісними, якщо хоч одне з чисел 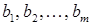 відмінне від 0.
відмінне від 0.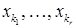 називаються головними невідомими, а всі інші невідомі – вільними невідомими.
називаються головними невідомими, а всі інші невідомі – вільними невідомими.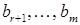 хоч одне відмінне від 0. Тоді система (1) містить рівняння
хоч одне відмінне від 0. Тоді система (1) містить рівняння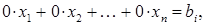
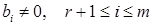 .
.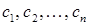 не задовольняє рівняння. Отже, система (1) розв¢язків немає. Тобто (1) – несумісна система.
не задовольняє рівняння. Отже, система (1) розв¢язків немає. Тобто (1) – несумісна система.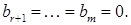 Для зручності подальших міркувань зробимо перепозначення невідомих
Для зручності подальших міркувань зробимо перепозначення невідомих 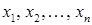 буквами
буквами 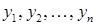 , так щоб головні невідомі
, так щоб головні невідомі 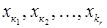 були позначені відповідно через
були позначені відповідно через 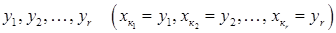 , а всі інші (тобто вільні невідомі) через інші
, а всі інші (тобто вільні невідомі) через інші 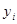 .
.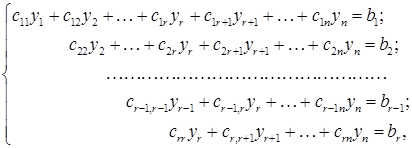 (2)
(2)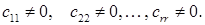
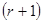 -го мали вигляд
-го мали вигляд 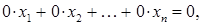 і тому ми їх опустили, оскільки при вилученні нуль-рівнянь (рівнянь виду
і тому ми їх опустили, оскільки при вилученні нуль-рівнянь (рівнянь виду 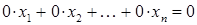 ) система переходить у рівносильну їй систему.)
) система переходить у рівносильну їй систему.)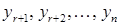 довільним чином конкретні числові значення
довільним чином конкретні числові значення 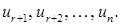 Тоді з останнього рівняння однозначно визначається
Тоді з останнього рівняння однозначно визначається 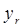 , а саме:
, а саме: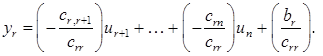
 (3)
(3)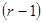 -го рівняння) можна однозначно визначити
-го рівняння) можна однозначно визначити 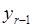 і т. д.
і т. д.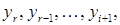 то з і -го рівняння
то з і -го рівняння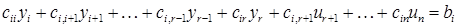
 визначається однозначно
визначається однозначно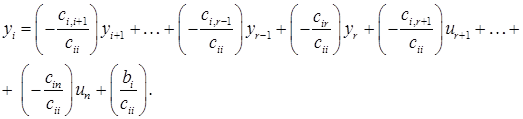
 тобто будуть однозначно визначені усі головні невідомі через числа
тобто будуть однозначно визначені усі головні невідомі через числа 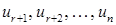 .
. система має єдиний розв¢язок, а при
система має єдиний розв¢язок, а при 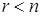 більше, ніж один розв¢язок. Зрозуміло, що усі розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти всі розв¢язки системи.
більше, ніж один розв¢язок. Зрозуміло, що усі розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти всі розв¢язки системи.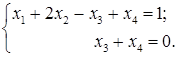
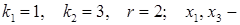 головні невідомі;
головні невідомі; 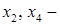 вільні невідомі). Нехай
вільні невідомі). Нехай 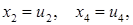 де
де 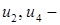 довільні числа. Тоді з останнього рівняння системи маємо
довільні числа. Тоді з останнього рівняння системи маємо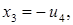
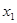 з першого рівняння
з першого рівняння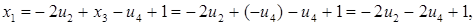
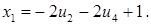
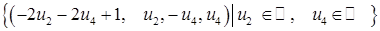 – множина усіх розв¢язків даної системи.
– множина усіх розв¢язків даної системи.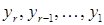 через вільні невідомі). В цьому пункті ми покажемо, що кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень може бути зведена до системи східчастого вигляду (прямий хід методу Гаусса). Враховуючи те, що елементарні перетворення переводять систему в рівносильну їй систему, ми одержимо таким чином загальний метод розв¢язування систем лінійних рівнянь. Він називається методом Гаусса.
через вільні невідомі). В цьому пункті ми покажемо, що кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень може бути зведена до системи східчастого вигляду (прямий хід методу Гаусса). Враховуючи те, що елементарні перетворення переводять систему в рівносильну їй систему, ми одержимо таким чином загальний метод розв¢язування систем лінійних рівнянь. Він називається методом Гаусса.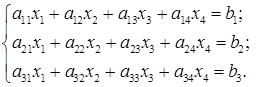 (S1)
(S1)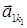 з найменшим номером
з найменшим номером 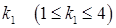 . Тоді наша система може бути записана у такому вигляді:
. Тоді наша система може бути записана у такому вигляді: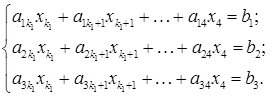 (S1¢)
(S1¢)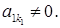 Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець
Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець 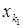 в другому і в третьому рівняннях зробити рівним 0, додамо до другого рівняння перше, помножене на
в другому і в третьому рівняннях зробити рівним 0, додамо до другого рівняння перше, помножене на 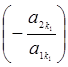 , а до третього додамо перше, помножене на
, а до третього додамо перше, помножене на 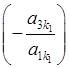 . Таким чином, здійснивши дані елементарні перетворення, ми одержимо систему, в якій
. Таким чином, здійснивши дані елементарні перетворення, ми одержимо систему, в якій 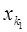 входить тільки до першого рівняння:
входить тільки до першого рівняння: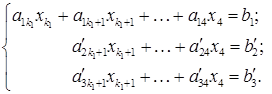 (S2)
(S2)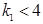 або
або 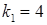 . Якщо
. Якщо 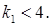
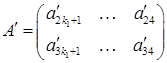
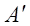 ненульова. Тоді в матриці
ненульова. Тоді в матриці 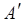 хоча б один стовпець ненульовий. Номери стовпців матриці
хоча б один стовпець ненульовий. Номери стовпців матриці 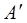 змінюються від
змінюються від 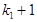 до 4. Серед усіх ненульових стовпців матриці
до 4. Серед усіх ненульових стовпців матриці 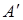 виберемо стовпець з найменшим номером
виберемо стовпець з найменшим номером 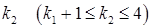 . Тоді система (S2) має вигляд
. Тоді система (S2) має вигляд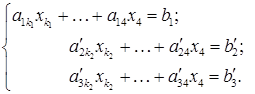 (S2¢)
(S2¢)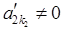 . Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець
. Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець 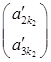 ненульовий. Для того, щоб у третьому рівнянні системи (S2¢) коефіцієнт при
ненульовий. Для того, щоб у третьому рівнянні системи (S2¢) коефіцієнт при 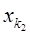 зробити рівним 0, додамо до третього рівняння друге, помножене на
зробити рівним 0, додамо до третього рівняння друге, помножене на 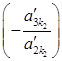 . Таким чином, здійснивши елементарне перетворення над системою (S2¢), ми одержимо систему східчастого вигляду.
. Таким чином, здійснивши елементарне перетворення над системою (S2¢), ми одержимо систему східчастого вигляду. , то вона є східчастою.
, то вона є східчастою.
 шляхом елементарних перетворень зводиться до східчастої.
шляхом елементарних перетворень зводиться до східчастої.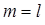 шляхом елементарних перетворень зводиться до східчастої.
шляхом елементарних перетворень зводиться до східчастої. рівнянь
рівнянь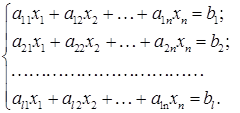 (1)
(1)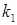 – найменший номер серед номерів ненульових стовпців матриці А. Тоді система (1) має вигляд:
– найменший номер серед номерів ненульових стовпців матриці А. Тоді система (1) має вигляд: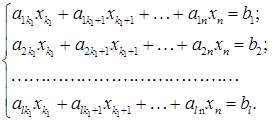 (2)
(2)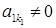 . Цього можна завжди домогтися шляхом елементарного перетворення перестановки рівнянь системи, оскільки
. Цього можна завжди домогтися шляхом елементарного перетворення перестановки рівнянь системи, оскільки 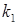 – ий стовпець матриці системи ненульовий.
– ий стовпець матриці системи ненульовий.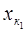 стали нульовими:
стали нульовими: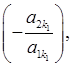
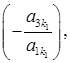 і т. д.,
і т. д., го рівняння додамо перше, помножене на
го рівняння додамо перше, помножене на 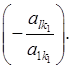
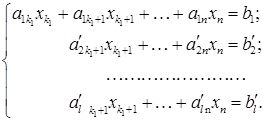 (3)
(3)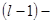 го рівняння наше припущення, отримаємо що та система шляхом елементарних перетворень зводиться до східчастого вигляду:
го рівняння наше припущення, отримаємо що та система шляхом елементарних перетворень зводиться до східчастого вигляду: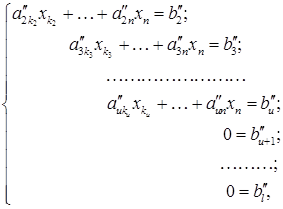 (4)
(4)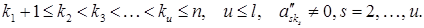
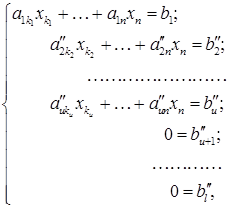 (5)
(5)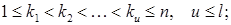
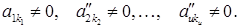
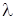 :
: