
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементарні перетворення системи лінійних рівнянь
Сумою лінійних рівнянь
Добутком лінійного рівняння Нехай маємо дві системи з однаковим числом невідомих. Кажуть, що друга система утворена з першої за допомогою елементарного перетворення типу А, якщо другу систему можна одержати з першої переставлянням місцями в першій системі її cистема 1 ~
Кажуть, що друга система утворена з першої за допомогою елементарного перетворення типу В, якщо другу систему можна одержати з першої заміною система 1 ~ система 2.
Зауваження. Легко бачити, що якщо з першої системи можна одержати другу за допомогою перетворення Приклад.
~ Теорема. Елементарні перетворення переводять систему лінійних рівнянь в рівносильну їй систему. Перед доведенням цієї теореми доведемо допоміжну лему. Лема. Якщо друга система лінійних рівнянь одержується з першої за допомогою елементарного перетворення, то кожен розв¢язок першої системи є розв¢язком другої. Доведення. У випадку елементарного перетворення типу А твердження леми очевидне. Нехай перша система лінійних рівнянь має вигляд де Помножимо почастинно Додамо почастинно до і -тої рівності з (2) останню рівність, одержимо правильну числову рівність
тобто Отже, правильними є наступі числові рівності
Всі рівності в (4) ті самі, що і в (2), лише і -та рівність замінена рівністю (3). Отже, Лему доведено. Доведення теореми. Нехай друга система лінійних рівнянь одержується з першої за допомогою елементарного перетворення, тоді і перша система одержується з другої за допомогою елементарного перетворення (див. зауваження після означення елементарного перетворення типу B). Тоді за лемою кожен розв¢язок першої системи є розв¢язком другої системи, і навпаки, кожен розв¢язок другої системи є розв¢язком першої системи. Теорему доведено.
Східчасті системи
Східчастою називається така система лінійних рівнянь, матриця якої є східчастою, тобто це система, яка має наступний вигляд:
де або система вигляду тобто система називається східчастою, якщо у розширеній її матриці
Приклади східчастих систем: 1). 2). 3). Системи виду Тому розглянемо системи виду (1). В такій системі невідомі Розглянемо два випадки: І. Нехай серед чисел
де Зрозуміло, що жодна сукупність чисел ІІ. Нехай
У відповідності до цього елементи матриці А системи (1) будуть перепозначені на елементи матриці С, тобто система (1) матиме наступний вигляд: де (Рівняння системи (1), починаючи з Надамо вільним невідомим Тоді з попереднього рівняння ( Якщо вже визначені
Так, рухаючись вгору по системі, будуть однозначно визначені Отже, система (2), а тому і система (1) є сумісними, причому при Приклад. Нехай маємо систему
Ця система східчаста і має вигляд (1) (
а тоді можна визначити
тобто Таким чином,
2.5. Зведення системи лінійних рівнянь до східчастого вигляду (метод Гаусса)
В пункті 2.4 було наведено метод розв¢язання східчастих систем (обернений хід методу Гаусса – послідовне знаходження головних невідомих Теорема. Кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень зводиться до системи східчастого вигляду.
Доведення теореми для випадку системи з трьох рівнянь з чотирма невідомими. Спочатку ми доведемо цю теорему для випадку системи, що складається з 3-ох рівнянь і має 4-и невідомі. Справді, нехай маємо систему: Будемо вважати, що матриця даної системи не є нуль-матрицею, бо інакше система вже мала б східчастий вигляд. Тоді серед усіх стовпців матриці А існує ненульовий стовпець Причому можна вважати, що
Можливі випадки Якщо матриця
нульова, то система (S2) вже має східчастий вигляд. Розглянемо випадок, коли така матриця Причому можна вважати, що Теорему для даного випадку доведено. Доведення теореми для загального випадку. Доведення проводимо індукцією за числом рівнянь даної системи. 1). Якщо система складається лише з одного рівняння 2). Припустимо, що система з числом рівнянь 3). Покажемо, що тоді і система з числом рівнянь
Справді, нехай маємо систему, що має Якщо матриця даної системи є нуль-матрицею, то система (1) є східчастою. Тому вважатимемо, що матриця системи (1) не є нуль-матрицею. Тоді вона має ненульовий стовпець. Нехай Можна вважати, що Зробимо над системою (2) такі елементарні перетворення (типу В), щоб в усіх рівняннях, починаючи з 2-го, коефіцієнти при
до 3-го рівняння додамо перше, помножене на до Отримаємо таку систему:
Використовуючи до системи з останніх де Тому і вся система (3) зведеться до східчастого вигляду: де Теорему доведено.
Вправи
1. Дослідити систему рівнянь і знайти її розв’язки в залежності від значень параметра
2. Переконатися, що елементарні перетворення одержати, помноживши її зліва на одиничну матрицю k -го порядку, над якою виконано відповідне перетворення. 3. Довести, що будь-яку матрицю, елементами якої є цілі числа, можна звести елементарними перетвореннями до східчастого вигляду (при цьому рядки можна множити лише на цілі числа). 4. Якщо кількість невідомих лінійної системи більша від кількості рівнянь, то система не може мати єдиного розв’язку. Довести.
|
||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.237.3 (0.081 с.) |
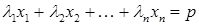 і
і  називається лінійне рівняння
називається лінійне рівняння 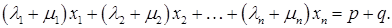
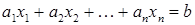 на число
на число 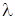 називається лінійне рівняння
називається лінійне рівняння 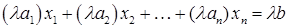 .
.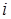 -го і
-го і 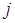 -го рівнянь
-го рівнянь 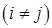 . Таке перетворення позначають через
. Таке перетворення позначають через 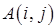 і записують:
і записують: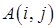
 cистема 2.
cистема 2.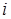 -го рівняння першої системи сумою її
-го рівняння першої системи сумою її 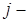 го рівняння, помноженого на деяке число
го рівняння, помноженого на деяке число  . Таке перетворення позначають через
. Таке перетворення позначають через 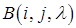 і записують:
і записують: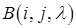
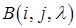 ), то з другої системи можна одержати першу за допомогою перетворення
), то з другої системи можна одержати першу за допомогою перетворення  (відповідно
(відповідно 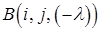 ). Перевірку виконати самостійно!
). Перевірку виконати самостійно!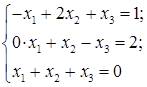 ~
~ 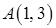
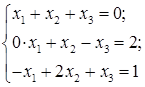

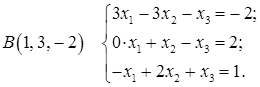
 (1)
(1)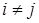 , а друга система одержується з першої за допомогою елементарного перетворення
, а друга система одержується з першої за допомогою елементарного перетворення 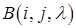 , де
, де 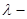 деяке число. Нехай також
деяке число. Нехай також 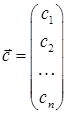 – розв’язок першої системи, тоді є правильними наступні числові рівності:
– розв’язок першої системи, тоді є правильними наступні числові рівності: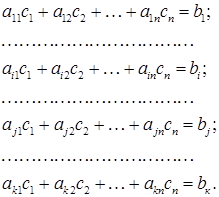 (2)
(2)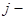 ту рівність з (2) на
ту рівність з (2) на 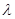 і одержимо правильну числову рівність
і одержимо правильну числову рівність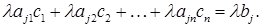
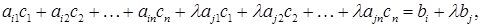
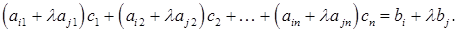 (3)
(3)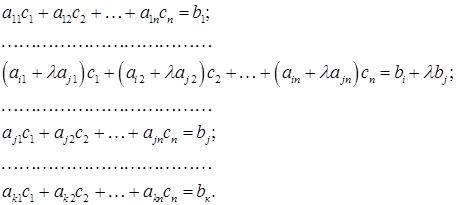 (4)
(4)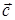 є також і розв¢язком тої системи, що одержана із системи (1) за допомогою елементарного перетворення
є також і розв¢язком тої системи, що одержана із системи (1) за допомогою елементарного перетворення 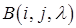 .
.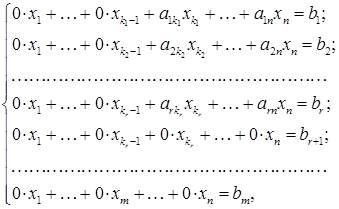 (1)
(1)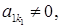
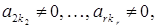
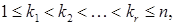


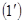
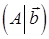 матриця А східчаста.
матриця А східчаста.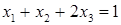 – східчаста система, що складається з одного рівняння (тут
– східчаста система, що складається з одного рівняння (тут 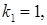
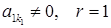 ).
).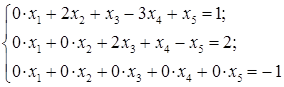 – східчаста система (тут
– східчаста система (тут 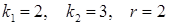 ).
).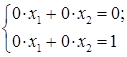 – східчаста система (тут
– східчаста система (тут 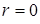 ).
).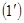 мають множину розв¢язків, що складається з усіх векторів
мають множину розв¢язків, що складається з усіх векторів 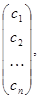 де
де 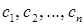 - довільні числа, якщо
- довільні числа, якщо 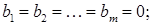 системи виду
системи виду 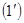 є несумісними, якщо хоч одне з чисел
є несумісними, якщо хоч одне з чисел 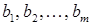 відмінне від 0.
відмінне від 0.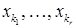 називаються головними невідомими, а всі інші невідомі – вільними невідомими.
називаються головними невідомими, а всі інші невідомі – вільними невідомими.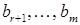 хоч одне відмінне від 0. Тоді система (1) містить рівняння
хоч одне відмінне від 0. Тоді система (1) містить рівняння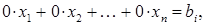
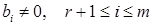 .
.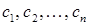 не задовольняє рівняння. Отже, система (1) розв¢язків немає. Тобто (1) – несумісна система.
не задовольняє рівняння. Отже, система (1) розв¢язків немає. Тобто (1) – несумісна система.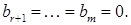 Для зручності подальших міркувань зробимо перепозначення невідомих
Для зручності подальших міркувань зробимо перепозначення невідомих 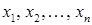 буквами
буквами 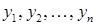 , так щоб головні невідомі
, так щоб головні невідомі 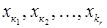 були позначені відповідно через
були позначені відповідно через 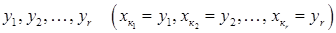 , а всі інші (тобто вільні невідомі) через інші
, а всі інші (тобто вільні невідомі) через інші 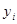 .
.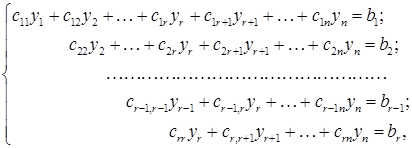 (2)
(2)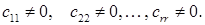
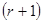 -го мали вигляд
-го мали вигляд 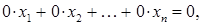 і тому ми їх опустили, оскільки при вилученні нуль-рівнянь (рівнянь виду
і тому ми їх опустили, оскільки при вилученні нуль-рівнянь (рівнянь виду 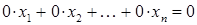 ) система переходить у рівносильну їй систему.)
) система переходить у рівносильну їй систему.)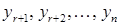 довільним чином конкретні числові значення
довільним чином конкретні числові значення 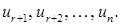 Тоді з останнього рівняння однозначно визначається
Тоді з останнього рівняння однозначно визначається 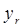 , а саме:
, а саме: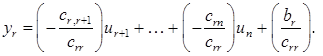
 (3)
(3)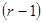 -го рівняння) можна однозначно визначити
-го рівняння) можна однозначно визначити 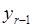 і т. д.
і т. д.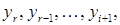 то з і -го рівняння
то з і -го рівняння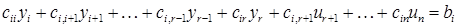
 визначається однозначно
визначається однозначно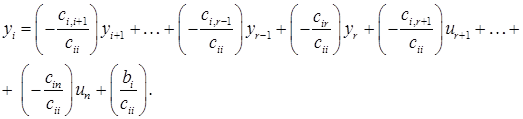
 тобто будуть однозначно визначені усі головні невідомі через числа
тобто будуть однозначно визначені усі головні невідомі через числа 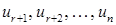 .
. система має єдиний розв¢язок, а при
система має єдиний розв¢язок, а при 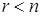 більше, ніж один розв¢язок. Зрозуміло, що усі розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти всі розв¢язки системи.
більше, ніж один розв¢язок. Зрозуміло, що усі розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти всі розв¢язки системи.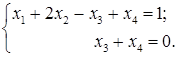
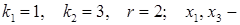 головні невідомі;
головні невідомі; 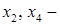 вільні невідомі). Нехай
вільні невідомі). Нехай 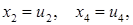 де
де 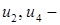 довільні числа. Тоді з останнього рівняння системи маємо
довільні числа. Тоді з останнього рівняння системи маємо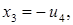
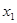 з першого рівняння
з першого рівняння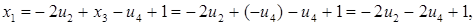
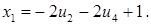
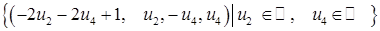 – множина усіх розв¢язків даної системи.
– множина усіх розв¢язків даної системи. через вільні невідомі). В цьому пункті ми покажемо, що кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень може бути зведена до системи східчастого вигляду (прямий хід методу Гаусса). Враховуючи те, що елементарні перетворення переводять систему в рівносильну їй систему, ми одержимо таким чином загальний метод розв¢язування систем лінійних рівнянь. Він називається методом Гаусса.
через вільні невідомі). В цьому пункті ми покажемо, що кожна система лінійних рівнянь за допомогою скінченного числа елементарних перетворень може бути зведена до системи східчастого вигляду (прямий хід методу Гаусса). Враховуючи те, що елементарні перетворення переводять систему в рівносильну їй систему, ми одержимо таким чином загальний метод розв¢язування систем лінійних рівнянь. Він називається методом Гаусса.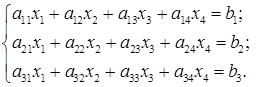 (S1)
(S1)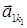 з найменшим номером
з найменшим номером 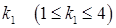 . Тоді наша система може бути записана у такому вигляді:
. Тоді наша система може бути записана у такому вигляді: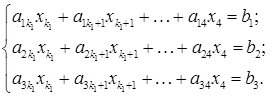 (S1¢)
(S1¢)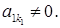 Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець
Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець 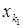 в другому і в третьому рівняннях зробити рівним 0, додамо до другого рівняння перше, помножене на
в другому і в третьому рівняннях зробити рівним 0, додамо до другого рівняння перше, помножене на 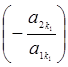 , а до третього додамо перше, помножене на
, а до третього додамо перше, помножене на 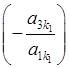 . Таким чином, здійснивши дані елементарні перетворення, ми одержимо систему, в якій
. Таким чином, здійснивши дані елементарні перетворення, ми одержимо систему, в якій 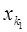 входить тільки до першого рівняння:
входить тільки до першого рівняння: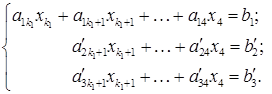 (S2)
(S2)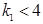 або
або 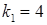 . Якщо
. Якщо 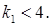
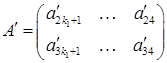
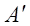 ненульова. Тоді в матриці
ненульова. Тоді в матриці 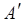 хоча б один стовпець ненульовий. Номери стовпців матриці
хоча б один стовпець ненульовий. Номери стовпців матриці 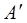 змінюються від
змінюються від 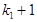 до 4. Серед усіх ненульових стовпців матриці
до 4. Серед усіх ненульових стовпців матриці 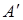 виберемо стовпець з найменшим номером
виберемо стовпець з найменшим номером 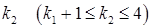 . Тоді система (S2) має вигляд
. Тоді система (S2) має вигляд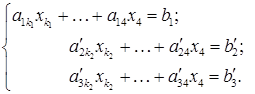 (S2¢)
(S2¢)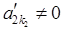 . Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець
. Цього можна завжди домогтися перестановкою рівнянь (елементарне перетворення), оскільки стовпець 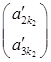 ненульовий. Для того, щоб у третьому рівнянні системи (S2¢) коефіцієнт при
ненульовий. Для того, щоб у третьому рівнянні системи (S2¢) коефіцієнт при 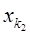 зробити рівним 0, додамо до третього рівняння друге, помножене на
зробити рівним 0, додамо до третього рівняння друге, помножене на 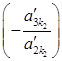 . Таким чином, здійснивши елементарне перетворення над системою (S2¢), ми одержимо систему східчастого вигляду.
. Таким чином, здійснивши елементарне перетворення над системою (S2¢), ми одержимо систему східчастого вигляду.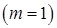 , то вона є східчастою.
, то вона є східчастою.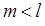
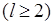 шляхом елементарних перетворень зводиться до східчастої.
шляхом елементарних перетворень зводиться до східчастої.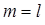 шляхом елементарних перетворень зводиться до східчастої.
шляхом елементарних перетворень зводиться до східчастої.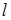 рівнянь
рівнянь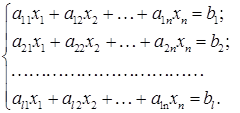 (1)
(1)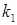 – найменший номер серед номерів ненульових стовпців матриці А. Тоді система (1) має вигляд:
– найменший номер серед номерів ненульових стовпців матриці А. Тоді система (1) має вигляд: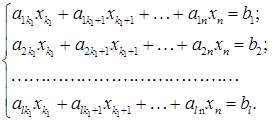 (2)
(2)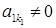 . Цього можна завжди домогтися шляхом елементарного перетворення перестановки рівнянь системи, оскільки
. Цього можна завжди домогтися шляхом елементарного перетворення перестановки рівнянь системи, оскільки 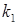 – ий стовпець матриці системи ненульовий.
– ий стовпець матриці системи ненульовий.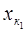 стали нульовими:
стали нульовими: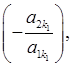
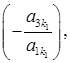 і т. д.,
і т. д.,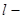 го рівняння додамо перше, помножене на
го рівняння додамо перше, помножене на 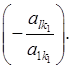
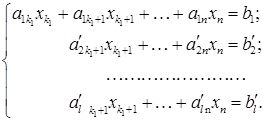 (3)
(3)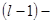 го рівняння наше припущення, отримаємо що та система шляхом елементарних перетворень зводиться до східчастого вигляду:
го рівняння наше припущення, отримаємо що та система шляхом елементарних перетворень зводиться до східчастого вигляду: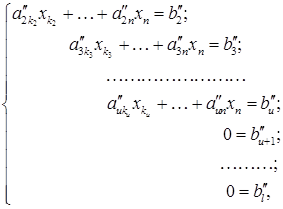 (4)
(4)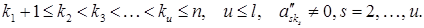
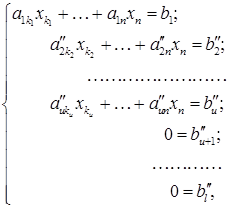 (5)
(5)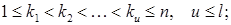
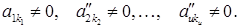
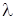 :
: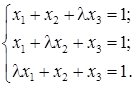
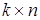 -матриці можна
-матриці можна


