
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1. Матриці та дії над ними
Означення матриць
Матрицею називається прямокутна таблиця, що заповнена певними математичними об’єктами, які називаються елементами матриці. Тут будемо розглядати лише такі матриці, елементами яких є числа. Елементи матриці будемо позначати однією буквою з двома індексами, де перший індекс вказує номер рядка елемента матриці, а другий – номер його стовпця. Таким чином, матриця записується у формі:
Якщо матриця має k рядків і n стовпців, то про таку матрицю кажуть, що вона має розмір k × n. Якщо кількість рядків і кількість стовпців матриці рівні, то така матриця називається квадратною, а кількість її рядків (стовпців) називається її порядком. Матрицю також позначають великими латинськими літерами або за допомогою відповідних малих літер з двома індексами: А = Дві матриці однакових розмірів називають рівними, якщо їх відповідні елементи рівні. Наприклад, матриці A = не є рівними (А ≠ В), оскільки
Види матриць
Матриця, що складається з одного рядка [стовпця], називається матрицею-рядком [ матрицею-стовпцем ]. Матрицю-рядок також називають рядком, а матрицю-стовпець – стовпцем. Використовуються також наступні терміни: вектор-рядок, вектор-стовпець. Вектор, що складається з n елементів, називається n -вимірним. Матриця О довільних розмірів, всі елементи якої дорівнюють нулю, називається нуль-матрицею: О =
Рядок [стовпець], всі елементи якого є нулі, називається нульовим рядком [стовпцем] або нуль-вектором. Одиничною матрицею називається квадратна матриця Е n -го порядку наступного вигляду:
Е =
де Квадратна матриця D називається діагональною, якщо вона має наступний вигляд: D = тобто dij = 0, якщо і ¹ j. Таку матрицю також позначають наступним чином: D = dia g Наприклад, Зрозуміло, що одинична матриця є діагональною. Квадратна матриця А називається нижньою трикутною, якщо вона має вигляд: А = тобто аij = 0, якщо і < j. Квадратна матриця А називається верхньою трикутною, якщо вона має вигляд: А = тобто а ij = 0, якщо і > j.
Матриця, яка є або нуль-матрицею, або матрицею виду
де Приклади: 1). 2). 3). 4). 5). 6). Східчастою називають матрицю А, яка має наступні властивості: 1). Якщо і -ий рядок нульовий, то (ί +1)-ий рядок також нульовий; 2). Якщо перші ненульові елементи ί -го і (ί +1)-го рядків є в стовпцях Кі і Кі +1 відповідно, то Кі < Кі +1. Приклад.
Означення дій над матрицями
Сумою двох матриць однакових розмірів А і В називають матрицю С, кожний елемент якої дорівнює сумі відповідних елементів матриць А і В, тобто С = А + В = (або Добутком матриці А на число λ називають таку матрицю В, кожний елемент якої дорівнює добутку числа λ і відповідного елемента матриці А, тобто: В = λ А = λ (або Матрицю (-1) А позначатимемо через – А і називатимемо її матрицею, протилежною до матриці А. Під різницею матриць А і В (А – В) будемо розуміти суму А + (- В). Зрозуміло, що А – А = О, А + О = О +А = А для всякої матриці А і нуль-матриці О тих же розмірів. Транспонованою до матриці А розмірів k
Транспоновану матрицю позначають через А T, а елементи її через Приклад: А = Для введення добутку двох матриць визначимо спочатку добуток рядка і стовпця однакової довжини (рядок – лівий множник, стовпець – правий множник, бо порядок співмножників тут важливий!):
У результаті одержимо квадратну матрицю першого порядку, яку можна ототожнити з її єдиним елементом Нехай матриця А має розмір Добутком матриць А і В називається матриця С = АВ, що має розмір k
c ij = i =1,..., k; j =1,..., r. Приклади: 1). 2). 3). 4).
Нехай А – квадратна матриця n -го порядку, Е – одинична матриця n -го порядку, а О – квадратна нуль-матриця n -го порядку. Тоді легко перевірити, що: АЕ = ЕА = А, АО = ОА = О. Слід зауважити, що добуток двох ненульових матриць може бути нульовою матрицею (нуль-матрицею). Справді, Квадратна матриця В n -го порядку називається оберненою до квадратної матриці А n -го порядку, якщо АВ = ВА = Е. Обернену матрицю до матриці А позначають через Приклад. Нехай А =
1.4. Властивості додавання матриць та множення матриць на числа Додавання матриць та множення матриць на числа мають наступні властивості:
1. А + (В + С) = (А + В) + С (асоціативність); 2. А + О = О + А = А; 3. А + (- А) = (- А) + А = О; 4. А + В = В + А (комутативність); 5. 6. 7. ( 8. (для довільних матриць А, В, С однакових розмірів і для довільних чисел Доведемо властивості 1 і 7. Всі інші властивості доводяться аналогічно і залишаються для самостійного доведення читачу. 1. А + (В + С) = = = (тут ми використали асоціативність додавання чисел). 7. = (тут ми використали дистрибутивність множення відносно додавання для чисел).
Символи суми Суму 1). Очевидними також є й інші властивості символу суми: 2). 3). де Часто використовуються так звані подвійні суми, які необхідні для підсумовування доданків з двома індексами.
тобто для знаходження суми всіх елементів прямокутної таблиці (матриці):
Тут і, j називаються першим і другим індексами підсумовування відповідно. Очевидно, що сума S всіх елементів даної таблиці дорівнює S = де Тому (Знаходимо суму всіх сум елементів рядків). З другого боку,
(Знаходимо суму всіх сум елементів стовпців). Таким чином, має місце наступна властивість символу подвійної суми: 4). Взагалі кажучи, символ суми може записуватися у найрізноманітніших ситуаціях. Його ж зміст може бути зрозумілим з контексту. Тепер нам легко буде оперувати з матрицями. Наприклад, елемент добутку
|
||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.207.129 (0.063 с.) |

 або
або  .
. =
=  , В =
, В =  =
=  .
. , В =
, В = 
 = 8,
= 8,  = 1.
= 1. .
. = [
= [  ij],
ij], – символ Кронекера.
– символ Кронекера.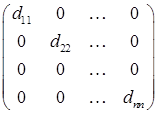 ,
,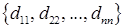 .
. .
.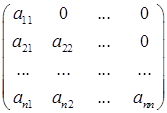 ,
, ,
, ,
,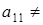 0,
0,  0,...,
0,...,  0 називають верхньою трапецієподібною матрицею.
0 називають верхньою трапецієподібною матрицею. ― нуль-матриця;
― нуль-матриця; ― вектор-стовпець;
― вектор-стовпець; ― діагональна матриця;
― діагональна матриця; ― одинична матриця;
― одинична матриця;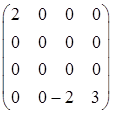 ― нижня трикутна матриця;
― нижня трикутна матриця; ,
, 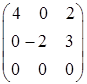 ,
,  ,
,  ― верхні трапецієподібні матриці.
― верхні трапецієподібні матриці. ― східчаста матриця, де
― східчаста матриця, де 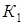 =2,
=2,  ,
,  .
.
 для всіх i, j).
для всіх i, j).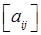 =
= 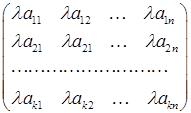 =
= 
 для всіх
для всіх  ).
). n називається така матриця В розмірів n
n називається така матриця В розмірів n  для всіх і, j. Тобто матриця В має за рядки відповідні стовпці матриці А.
для всіх і, j. Тобто матриця В має за рядки відповідні стовпці матриці А. (= а
(= а  ).
).


 =
= 
 Добуток АВ матриць А і В визначаємо тільки тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В.
Добуток АВ матриць А і В визначаємо тільки тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В. , а матриця В – n
, а матриця В – n  .
. дорівнює добутку і -го рядка матриці А і j -го стовпця матриці В:
дорівнює добутку і -го рядка матриці А і j -го стовпця матриці В: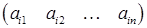
 =
= 

 =
=  ;
;

 ;
;
 =
=  ;
;



 .
. . Тоді В =
. Тоді В =  – обернена матриця до матриці А.
– обернена матриця до матриці А. А = А;
А = А; (А + В) =
(А + В) =  А +
А +  ) А =
) А =  ) А
) А  ,
,  ).
). +
+ 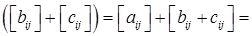

 =
= 



 позначають через
позначають через  , де і називається індексом підсумовування і його позначення ролі не відіграє, тобто його можна замінити будь-якою іншою буквою:
, де і називається індексом підсумовування і його позначення ролі не відіграє, тобто його можна замінити будь-якою іншою буквою: ;
; (адитивність);
(адитивність); (однорідність);
(однорідність);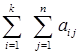











 матриць
матриць  і
і  розмірів
розмірів  і
і  , відповідно, записується наступним чином:
, відповідно, записується наступним чином: .
.


