
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирвование электротехнических комплексов в программе matlab .
2.1. АНАЛИЗ ПЕРЕХОДНЫХ
Рассмотрен пример использования пакета MatLab для расчета переходного процесса в электрической цепи с несколькими накопителями электрической энергии.
Анализ поведения многих систем и устройств в динамике, а также решение многих задач в теории колебаний и в поведении упругих оболочек обычно базируются на решении систем обыкновенных дифференциальных уравнений (ОДУ). Их, как правило, представляют в виде системы из дифференциальных уравнений первого порядка в форме Коши:
с граничными условиями Многообразие электротехнических устройств, конструкций, различие магнитных систем делают задачу анализа электрических цепей актуальной. Приведем пример расчета электрической цепи приведенной на рис. 2.1. Используя законы коммутации для электрической цепи можно составить математическую модель, описывающую процессы протекающие в рассматриваемой электрической цепи, причем
Для решения систем обыкновенных дифференциальных уравнений (ОДУ) в MatLab реализованы различные методы. Их реализации представляют собой решатели ОДУ. Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode15s, ode23s, ode23t, ode23tb [3]: · ode45- одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты; · ode23 – одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. При низких требованиях к точности этот метод может дать выигрыш в скорости решения; · ode113 – многошаговый метод Адамса-Башворта-Мултона переменного порядка. Адаптивный метод, который может обеспечить высокую точность решения;
· ode15s – многошаговый метод переменного порядка (от 1 до 5), использующий формулы численного дифференцирования. Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения; · ode23tb – неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем. Данный метод может оказаться более эффективным, чем ode15s; · ode23s – одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений. · ode23t – метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом; · bvp4c служит для проблемы граничных значений систем дифференциальных уравнений вида · pdepe нужен для решения систем параболических и эллиптических дифференциальных уравнений в частных производных, введен в ядро системы для поддержки графических функций OpenGL Все решатели могут решать системы уравнений явного вида Для расчета уравнения (2.1) хорошо зарекомендовали себя численные методы решения систем дифференциальных уравнений. Система уравнений (2.2) должна быть разрешена относительно неизвестных стоящих под знаком дифференциала, следовательно, необходимо дополнить (2.2) алгебраическими уравнениями:
Выполнив соответствующие преобразования (2.3) получим
Подготовим m-файл ode-функции для расчета электрической цепи (Литинг.2.1).
Данный текст программы должен быть сохранен в формате m-файла (текстового файла с расширением *.m). Запуск программы на расчет производится указанием в командном окне строки: [t,y]=ode45(@filename, [0 0.03], [0 0 0 0]), где @Filename – имя сохраненного m-файла с программой; [0 0.03] – время моделирования (в данном случае от 0 до 30 мс); [0 0 0 0] – начальные значения Результаты расчета приведены на рис. 2.2. Вопросы для самопроверки. 1. В чем особенности расчета переходных процессов в линейных электрических цепях? 2. Назовите наиболее распространенные методы расчета систем дифференциальных уравнений. 3. Укажите последовательность записей m-файла для расчета переходного процесса в линейных электрических цепях. 4. Какой командой в программе MatLab созданный m-файл запускается на выполнение? 5. Укажите команду для графического построения результатов расчета.
|
||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.237.255 (0.007 с.) |
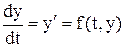 (2.1)
(2.1)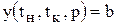 , где
, где 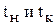 - начальные и конечные точки интервалов. Параметр t, как правило, означает время, так как решение дифференциальных уравнений ищется во временной области. Вектор b задает начальные и конечные условия.
- начальные и конечные точки интервалов. Параметр t, как правило, означает время, так как решение дифференциальных уравнений ищется во временной области. Вектор b задает начальные и конечные условия.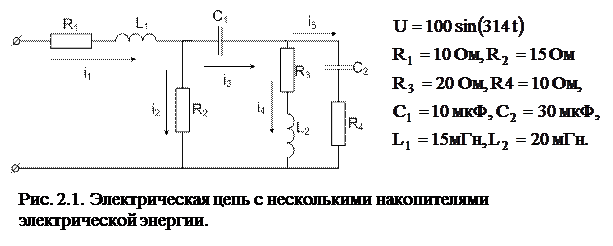 С учетом
С учетом 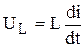 и
и 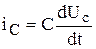 математическая модель будет представлена в виде системы уравнений (2.2)
математическая модель будет представлена в виде системы уравнений (2.2) (2.2)
(2.2)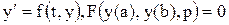 (краевая задача);
(краевая задача);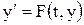 . Решатели ode15s и ode23t способны найти корни дифференциально-алгебраических уравнений
. Решатели ode15s и ode23t способны найти корни дифференциально-алгебраических уравнений  , где M – матрица массы. Решатели ode15s, ode23t и ode23tb могут решать уравнения неявного вида
, где M – матрица массы. Решатели ode15s, ode23t и ode23tb могут решать уравнения неявного вида 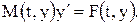 . Методы ode23s и ode23tb служат для решения жестких дифференциальных уравнений, ode15s – для решения жестких дифференциальных и дифференциально-алгебраических уравнений, ode23t – умеренно жестких дифференциальных и дифференциально-алгебраических уравнений.
. Методы ode23s и ode23tb служат для решения жестких дифференциальных уравнений, ode15s – для решения жестких дифференциальных и дифференциально-алгебраических уравнений, ode23t – умеренно жестких дифференциальных и дифференциально-алгебраических уравнений. (2.3)
(2.3)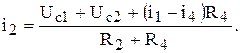 (2.4)
(2.4) Листинг 2.1.
Листинг 2.1.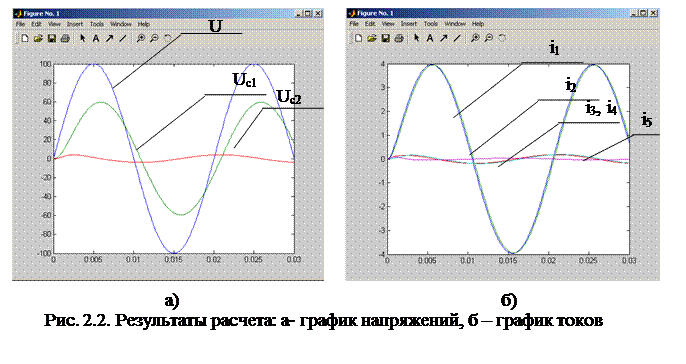
 .
.


