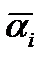Методические указания к выполнению задачи 1

 

Дефицит информации является наиболее характерной ситуацией при принятии решений. Один из методов принятия решений в этих случаях основывается на правилах теории игр и статистических решений, которые регламентируют: возможные варианты (стратегии) действия сторон, участвующих в игре; наличие и объем информации каждой стороны о поведении другой; результат игры, к которому приводит определенная стратегия ([5], § 2.5). Стратегия – это совокупность правил, предписывающих действия в зависимости от ситуации, сложившейся в ходе игры.

В качестве сторон в игре рассматриваются конкурирующие противники А и В или стороны А и П – «природа», например, организаторы производства; производственные ситуации; климатические условия и т.д. Отметим, что в реальных ситуациях поведение «природы» заранее неизвестно. Для этого случая при каждом сочетании стратегии стороны А и «природы» П определяется выигрыш.

Рассмотрим формирование рационального запаса узлов (агрегатов) на складе АТП. Допустим, что ежедневно при ремонте требуется не более 4 агрегатов, причем вероятность того, что агрегаты не потребуются для ремонта в течение смены, равна 0,1; потребуется один агрегат – 0,4; два – 0,3; три – 0,1 и четыре – 0,1. указанные вероятности можно рассматривать как вероятности реализации стратегий стороны П, причем первая стратегия П₁ состоит в том, что фактически потребуется для ремонта 0 агрегатов; вторая стратегия П₂ – один агрегат; третья стратегия П₃ – два агрегата; четвертая П₄ – три агрегата и пятая П₅ – четыре агрегата.

При организации на складе запаса можно применить следующие стратегии: А₁ – не иметь запаса; А₂ –иметь в запасе один агрегат (n₁=1); А₃ –иметь в запасе два агрегата; А₄ –иметь три агрегата и А₅ –иметь четыре агрегата.

Каждому сочетанию А _i и П _j стратегий соответствуют выигрыши а _ij, которые рассчитывают для стороны А из следующих условий: отсутствие необходимого агрегата как ущерб в три условные единицы (-3); хранение одного невостребованного узла оценивается как ущерб в одну единицу (-1); удовлетворение потребности в одном агрегате – как прибыль в две единицы (+2).

Отметим, что ущерб и прибыль должны быть обоснованы, так как от них зависит выбор рационального (или оптимального) решения. Для конкретного примера удовлетворение потребности в агрегатах связано с сокращением простоев автомобилей в ремонте, что приносит прибыль АТП. Излишний запас вызывает дополнительные затраты на хранение.

В табл. 6 приведена платежная матрица, составленная по условиям примера с формированием запасов агрегатов.

 

Таблица 6

Таблица выигрышей для сочетаний стратегий

 

Стратегия стороны А	Необходимое число агрегатов nj при стратегии Пj	Минимальный выигрыш по стратегиям (минимумы строк) ai
П1	П2	П3	П4	П5
n1=0	n2=1	n3=2	n4=3	n5=4
А1 (n1=0)		-3	-6	-9	-12	-12
А2 (n2=1)	-1		-1	-4	-7	-7
А3 (n3=2)	-2				-2	-2 (max aI =k1)
А4 (n4=3)	-3					-3
А5 (n5=4)	-4	-1				-4
Максимальный выигрыш (максимумы столбцов) b i

 

Например, при сочетании стратегий А₂ и П₄ (при потребности 3 на складе имеется 1 агрегат) выигрыш составит а₂₄ = 1х2 - 2х3 (две заявки не удовлетворены) = 2 - 6= - 4. При сочетании стратегий А₄ и П₂ (необходим для замены один агрегат, на складе имеется 3) выигрыш составит а₄₂ = 1х2 (удовлетворено одно требование) – 2х1 (два агрегата не востребованы) = 2-2=0 и т.д.

Наиболее простое решение возникает тогда, когда находится стратегия А _i, каждый выигрыш которой при любом сочетании П _j во всяком случае не меньше, чем выигрыш при любых других стратегиях. В рассматриваемом примере таких стратегий нет.

При известных вероятностях P _j каждого состояния P _j выбирается стратегия А _i, при которой математическое ожидание выигрыша будет максимальным. Для этого вычисляют средний выигрыш по каждой строке для i-й стратегии:

Оптимальной стратегии соответствует максимальное значение а₀.

В табл. 7 приведены результаты расчета выигрыша при различном сочетании стратегий А и состояний П.

Таблица 7

 

Матрица выигрышей

 

Стратегия стороны А	П1 (n1=0)	П2 (n2=1)	П3 (n3=2)	П4 (n4=3)	П5 (n5=4)	Средний выигрыш при стратегии
А1 (n1=0)		-3	-6	-9	-12	-5,1
А2 (n2=1)	-1		-1	-4	-7	-0,7
А3 (n3=2)	-2				-2	1,3
А4 (n4=3)	-3					1,5 =
А5 (n5=4)	-4	-1				1,1
Вероятности состояний Pj	0,1	0,4	0,3	0,1	0,1	-

Из анализа матрицы выигрышей следует, что оптимальной в данном примере является стратегия А₄, которая сводится к созданию фонда в три агрегата (n₄=3).

Данную методику можно использовать при определении оптимальной численности рабочих; пропускной способности СТО. При этом недостаточная пропускная способность приводит к простоям в ожидании ремонта автомобилей, с другой стороны, излишняя пропускная способность вызывает убытки.

Игровой подход возможен также при решении вопроса о методах ремонта автомобилей (стратегия А_i) в зависимости от его технического состояния (П_j); выбора метода улучшения производственной базы в зависимости от внешних условий (капиталовложения, расширение объема перевозок); определения числа постов технического обслуживания и т.д.

 

Задача 2

 

За 10 лет работы определить число замен подвижного состава АТП объемом А единиц при случайном списании автомобилей, если известно, что распределение наработок до списания подчиняется нормальному закону, который характеризуется средним сроком списания автомобилей Х лет и средним квадратическим отклонением срока их списания s. Исходные данные для решения задачи выбрать в табл. 8.

Таблица 8

 

Параметр	Последние цифры шифра зачетной книжки
Объем парка автомобилей, А, ед.	Статистические параметры срока списания автомобилей
Х, год	s,год
	5,0	1,0	00…09
	6,5	1,1	10…19
	7,0	0,7	20…29
	8,0	0,85	30…39
	5,5	0,8	40…49

 

Окончание табл. 8

	6,0	0,9	50…59
	7,5	0,95	60…69
	4,0	0,75	70…79
	4,5	1,05	80…89
	8,5	0,60	90…99