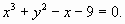Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными ⇐ ПредыдущаяСтр 5 из 5
Элементы математической статистики. Теорию вероятностей можно определить как раздел математики, в котором изучаются закономерности присущие массовым случайным явлениям. Методы теории вероятностей широко применяются при математической обработке результатов измерений, а также во многих задачах экономики, статистики, страхового дела, массового обслуживания. Вероятность – одно из основных понятий т.в. Существует несколько определений этого понятия. Приведем то, которое принято называть классическим. Р(А) = m/n, m- число иcходов, благоприятствующих А; n- число всех возможных исходов испытания. Основные формулы комбинаторики а) перестановки б) размещения в) сочетания Классическое определение вероятности. Вероятность суммы событий Теорема сложения вероятностей несовместных событий: Теорема сложения вероятностей совместных событий: Вероятность произведения событий Теорема умножения вероятностей независимых событий: Теорема умножения вероятностей зависимых событий: Формула полной вероятности 6. Формула Байеса (формула Бейеса). Вычисление апостериорных вероятностей гипотез
Формула Бернулли
Решение типовых примеров Пример 1. Даны два комплексных числа z1 = 2 – j 7 и z2 = 3 + j5. Требуется: 1) найти комплексные числа z = z1 + z2, u = z1 – z2, записав их в алгебраической форме; 2) найденные z1, z2, z, u изобразить на комплексной плоскости; 3) комплексные числа v =z1 ∙ z2, w =z1: z2 записать в тригонометрической и показательной формах.
Решение. 1). Для того, чтобы найти z = z1 + z2 в алгебраической форме, складываем действительные и мнимые части чисел z1 и z2: z = (2 – j 7) + (3 + j5) = (2 + 3) + j(–7 + 5) =5–j2. При нахождении числа u = z1 – z2 вычитаем действительные и мнимые части чисел z1 и z2: u = z1 – z2 = (2 – j 7) – (3 + j5) = (2–3) + j(–7–5) = –1–j12.
2). Вектор, соответствующий числу z, строим как сумму векторов z1 и z2 по правилу параллелограмма, а вектор, соответствующий числу u, строим как сумму векторов z1 и (– z2).
3). Найдем модуль r и аргумент φ чисел z1 и z2. z1 = 2 – j 7, число принадлежит IVчетверти, значит φ1 = – arctg r1 = z2 = 3 + j5, число принадлежит I четверти, значит φ2 = arctg r2 = Запишем числа z1 и z2 в показательной z = r ejφ и тригонометрической z = r (cosφ + j sinφ) формах: z1 = 8,06e-j74,05°, z1 = 8,06(cos (–74,05 °)+ j sin (–74,05 °)) z2 = 5,83ej59,04°, z2 = 5,83(cos 59,04 ° + j sin 59,04 °).
Найдем произведение и частное этих чисел: v = z1∙ z2 = 8,06∙5,83ej(-74,05°+59,04°) = 46,99e-j15,01° = 46,99(cos(–15,01°) + j sin(–15,01°)); w = z1: z2 = 8,06:5,83ej(-74,05°-59,04°) = 1,38e-j133,09° = 1,38(cos(–133,09°) + j sin(–133,09°)). Пример 2. Вычислить производную функции y=(3x3-2x+1)×sin x. Решение. По правилу 2, y'=(3x3-2x+1)'×sin x + (3x3-2x+1)×(sin x)' = = (9x2-2)sin x + (3x3-2x+1)cos x. Пример 3. Найти производную сложной функции y= Решение. По правилу дифференцирования сложной функции, получим: y'x =y 'u u'x =( Пример 4. Решить уравнение y' = xy Решение. Производную функции y' заменим на разделим переменные проинтегрируем обе части равенства:
Ответ: Пример 5. Найти частное решение уравнения
2yy' = 1- 3x2, если y0 = 3 при x0 = 1 Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Интегрируя обе части последнего равенства, найдем Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+ C, т.е. С = 9. Следовательно, искомый частный интеграл будет
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 51; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.50.206 (0.009 с.) |
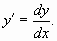
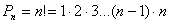 .
.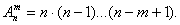
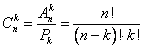 .
.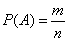 , где
, где  - число благоприятствующих событию
- число благоприятствующих событию  исходов,
исходов,  - число всех элементарных равновозможных исходов.
- число всех элементарных равновозможных исходов.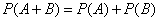
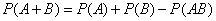

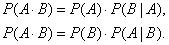 ,
,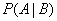 - условная вероятность события
- условная вероятность события 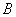 ,
,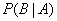 - условная вероятность события
- условная вероятность события  , где
, где 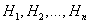 - полная группа гипотез, то есть
- полная группа гипотез, то есть 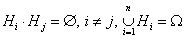 ,
,  - достоверное событие.
- достоверное событие.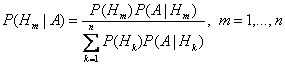 , где
, где 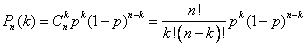 - вероятность появления события ровно
- вероятность появления события ровно 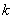 раз при
раз при 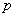 - вероятность появления события при одном испытании.
- вероятность появления события при одном испытании.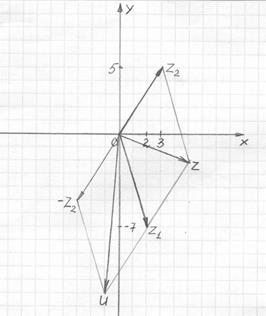
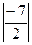 = – arctg3,5
= – arctg3,5 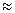 – 74,05°.
– 74,05°.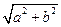 =
=  =
=  .
.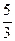
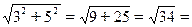 5,83.
5,83.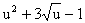 , u=x4 +1.
, u=x4 +1.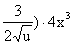 . Так как u=x4 +1, то y'x=(2 x4 +2+
. Так как u=x4 +1, то y'x=(2 x4 +2+  .
.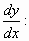
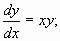
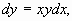

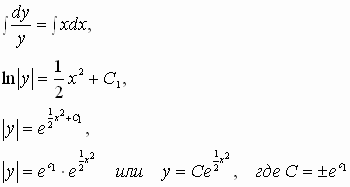
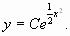
 Отсюда
Отсюда 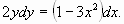
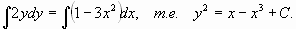
 или
или