
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для выполнения контрольной работыСтр 1 из 5Следующая ⇒
Методические указания Для выполнения контрольной работы по дисциплине МАТЕМАТИКА ЕН.01.Математический и общий естественнонаучный цикл
для специальностей Строительство и эксплуатация зданий и сооружений» Механизация сельского хозяйства» Числовые системы
Развитие понятия числа. Комплексные числа. Действия над комплексными числами. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами в тригонометрической и показательной формах.
Производная и её приложения
Свойства и графики основных элементарных функций. Понятия предела и непрерывности функции в точке. Основные свойства предела. Предел функции на бесконечности. Вычисление пределов. Производная, её геометрический и физический смысл. Правила дифференцирования. Дифференциал функции и его геометрический смысл. Возрастание и убывание функции. Экстремум функции. Вторая производная и её физический смысл. Выпуклость, точки перегиба графика функции. Исследование функций и построение графиков. Задачи на наибольшее и наименьшее значение.
Интеграл и его приложения
Первообразная. Неопределённый интеграл и его свойства. Основные табличные интегралы. Интегрирование подстановкой. Определённый интеграл и его геометрический смысл. Основные свойства и вычисление определённого интеграла. Вычисление площадей фигур с помощью определённого интеграла. Применение интеграла к решению физических задач. Дифференциальные уравнения.
Определение дифференциального уравнения, порядок уравнения. Начальные условия. Общее и частное решение дифференциального уравнения. Дифференциальные уравнения I порядка с разделяющимися переменными, техника их решения. Примеры уравнений I порядка, имеющих решения. Дифференциальные уравнения II порядка вида
Элементы математической статистики.
Область применения и задачи математической статистики. Понятие о генеральной совокупности и выборке, представительность выборки, способы её отбора. Статистическое распределение выборки. Первичная обработка статистических данных, элементы выборки,
формирование вариационного ряда. Статистическая оценка параметров распределения, формулы для их вычисления. Понятие о статистической проверке гипотез.
КОНТРОЛЬНАЯ РАБОТА
Задание 1
1.1. – 1.10. Выполните действия в алгебраической форме. Результат запишите в тригонометрической и показательной формах:
1.11. – 1.14. Выполните действия в тригонометрической форме. Результат запишите в алгебраической и показательной формах: 1.11. 4(cos 220o + i sin 220o) · 1,5(cos 20o + i sin 20o). 1.12. 3(cos 280o + i sin 280o): 1. 13. (2(cos 50o + i sin 50o))6 1.14. 3(cos 340o + i sin 340o):
1.15 – 1.20. Запишите комплексное число в тригонометрической и алгебраической формах:
Задание 2
2.1. Найдите производную функции 2.2. Найдите производную функции 2.3. Найдите производную функции у = 2.4. Найдите производную функции s = 2.5. Найдите производную функции 2.6. Найдите производную функции 2.7. Найдите производную функции 2.8. Найдите производную функции 2.9. Найдите производную функции у = tg2 x – ctg2 x и вычислите 2.10. Найдите производную функции у = sin4 x cos 4x и вычислите 2.11. Найдите производную функции s = 2.12. Найдите производную функции 2.13. Найдите вторую производную функции 2.14. Найдите производную функции у = 2.15. Найдите производную функции 2.16. Найдите производную функции 2.17. Найдите вторую производную функции у = 2.18. Найдите вторую производную функции 2.19. Найдите производную функции 2.20. Найдите вторую производную функции Задание 3
3.1. – 3.20. Найдите неопределённые интегралы:
Задание 4
4.1. – 4.20. Вычислите определённые интегралы:
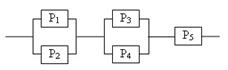
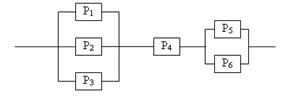
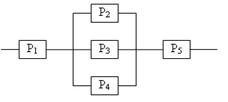
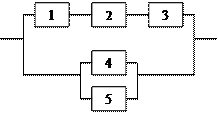
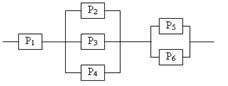
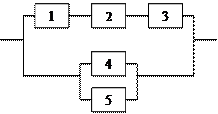
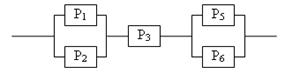
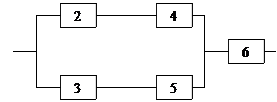
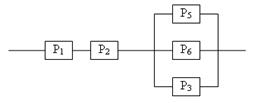
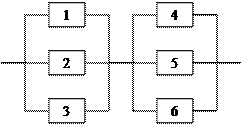
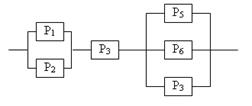
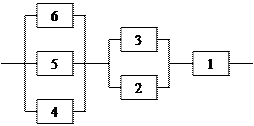
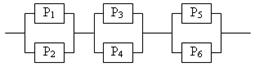
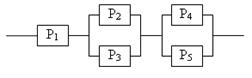
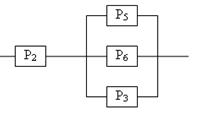
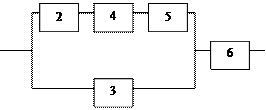
Задание 5 5.1. – 5.20. Найти вероятность безотказной работы участка цепи, если известно, что каждый i-ый элемент работает независимо от других с вероятностью pi (i = 1, 2, 3, 4, 5, 6). p1 = 0,7, p2 = 0,7, p3 = 0,6, p4 = 0,8, p5 = 0,5, p6 = 0,9.
Задание 6 Дан ряд распределения дискретной случайной величины Y. Определить математическое ожидание и дисперсию случайной величины.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19.
6.20.
Задание 7
7.1.– 7.20. Даны два комплексных числа z1 и z2. Требуется: 1) найти комплексные числа z = z1 + z2, u = z1 – z2, записав их в алгебраической форме; 2) найденные z1, z2, z, u изобразить на комплексной плоскости; 3) комплексные числа v = z1 ∙ z2, w = z1: z2 записать в тригонометрической и показательной формах.
Задание 8
8.1. В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым)? 8.2. В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Используя классическое определение теории вероятности определить, какова вероятность того, что обе детали окажутся бракованными.
8.3. Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получится слово «книга». 8.4. В урне лежат 20 одинаковых на ощупь шаров: 12 белых и 8 черных. Какова веро-ятность вынуть наудачу два белых шара? 8.5. В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым. 8.6. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему три вопроса? 8.7. На карточках написаны целые числа от 1 до 15 включительно. Наудачу извлекаются две карточки. Какова вероятность того, что сумма чисел, написанных на карточках, равна десяти? 8.8. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что набраны нужные цифры. 8.9. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара?
8.10. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность того, что оба шара окажутся белыми?
Методические указания к выполнению контрольной работы Числовые системы Уравнение вида х2 + 1 = 0 не имеет решений на множестве R действительных чисел. Поэтому множество R приходится расширять до нового множества, такого, чтобы в этом множестве уравнения вида х2 + а2 = 0 имели решение. х2 + 1 = 0 => х2 = - 1 – мнимая единица, обозначение: j 2 = -1. Комплексным числом называется выражение вида z = а + jb, а – действительная часть комплексного числа, а число jb – мнимая часть. Свойства комплексных чисел: 1. а1 + jb1 = а2 + jb2, если а1= а2, b1= b2. 2. z = 0 + j0 = 0 – нуль. 3. z = а + j0 = а. 4. z = 0 + jb = jb – чисто мнимое число. Геометрическая интерпретация комплексного числа.
числу а, ось У – мнимая ось, соответствует числу b. Модуль комплексного числа: r = ׀ z ׀ = Аргумент комплексного числа: arg z = φ – угол между положительным направлением оси Х (абсцисс) и вектором, соответствующим комплексному числу.
Алгоритм нахождения аргумента числа z = а + j b.
1. находим α = arсtg ׀ 2. определяем в какой четверти находится число z по таблице:
3. вычисляем φ: если z лежит в I четверти, то φ = α, если z лежит во II четверти, то φ = π - α, если z лежит в III четверти, то φ = π + α, если z лежит в IV четверти, то φ = 2 π – α. Формы записи комплексных чисел. 1. алгебраическая: z = а + jb, где а и b – действительные числа; 2. тригонометрическая: z = r (cos φ + j sin φ ), где r – модуль комплексного числа, φ – аргумент. 3. показательная: z = r ejφ, где r – модуль комплексного числа, φ – аргумент. Действия над комплексными числами. 1. В алгебраической форме правила те же, что и на множестве R. При делении числитель и знаменатель домножаются на число, сопряженное знаменателю. 2. В тригонометрической форме: z1 = r1 (cos φ1 + j sin φ1), z2 = r2 (cos φ2 + j sin φ 2) а) z1٠ z2 = r1 ٠ r2 (cos(φ1+ φ 2)+ j sin(φ1+ φ 2)) б) в) zn = rn (cos nφ + j sin nφ) г) 3. В показательной форме: z = r1 ejφ, z2 = r ejφ а) z1٠ z2 = r1 ٠ r2 ej(φ+φ) б) в) zn = rn ٠ ejnφ г), При переводе из тригонометрической и показательной форм в алгебраическую используются формулы: a = r ٠cos φ b = r ٠ sin φ.
Производная и её приложения Понятие производной является одним из фундаментальных понятий математики. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов. Пусть функция y = - аргументу x - найдем соответствующее приращение функции: - составим отношение приращения функции к приращению аргумента: - найдем предел этого отношения при Если этот предел существует, то его называют производной функции Производной функции y =
Функция y = Производная суммы, разности, произведения и частного функций. Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул. Пусть функции 2. 3. 4. Производная сложной функции. Если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то
Интеграл и его приложения
Интегральное исчисление - это раздел математического анализа, в котором изучаются интегралы, их свойства, способы вычисления и приложения. Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа. Центральным в интегральном исчислении является понятие интеграла, которое, однако, имеет две различные трактовки, приводящие соответственно к понятиям неопределенного и определенного интегралов. Рассматриваемая в интегральном исчислении математическая операция (обратная к дифференцированию) называется интегрированием или, точнее, неопределенным интегрированием. Если F (x) - первообразная для f (x) на промежутке X, то множество всех первообразных для f (x) имеет вид F (x) + C, где C - любое действительное число. Табличные интегралы
Правила интегрирования
Дифференциальные уравнения. Многочисленные задачи естествознания, техники и других областей знания сводятся к тому, что по заданным свойствам некоторого процесса или явления необходимо найти математическую модель самого процесса в виде формулы, связывающей переменные величины, т.е. в виде функциональной зависимости. Уравнения, в которых содержатся производные или дифференциалы искомых функций, называются дифференциальными. Они являются мощным средством познания окружающего нас мира. Дифференциальное уравнение - это как бы мгновенный снимок процесса в данный момент времени, интегрируя дифференциальное уравнение, мы по мгновенным снимкам восстанавливаем течение процесса в целом. Уравнения вида dy / dx = f (x)/ g (y) можно решить, записав его в дифференциалах g (y) dy = f (x) dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy / dx = x / y имеем f (x) = x, g (y) = y. Записав его в виде ydy = xdx и проинтегрировав, получим y 2 = x 2 + c. Дифференциальное уравнение вида
или
называется дифференциальным уравнением с разделяющимися переменными. Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных. Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем два неопределенных интеграла. Вероятность суммы событий Теорема сложения вероятностей несовместных событий: Теорема сложения вероятностей совместных событий: Формула полной вероятности 6. Формула Байеса (формула Бейеса). Вычисление апостериорных вероятностей гипотез Формула Бернулли
Решение типовых примеров Пример 1. Даны два комплексных числа z1 = 2 – j 7 и z2 = 3 + j5. Требуется: 1) найти комплексные числа z = z1 + z2, u = z1 – z2,записав их в алгебраической форме; 2) найденные z1, z2, z, u изобразить на комплексной плоскости; 3) комплексные числа v =z1 ∙ z2, w =z1: z2 записать в тригонометрической и показательной формах.
Решение. 1). Для того, чтобы найти z = z1 + z2 в алгебраической форме, складываем действительные и мнимые части чисел z1 и z2: z = (2 – j 7) + (3 + j5) = (2 + 3) + j(–7 + 5) =5–j2. При нахождении числа u = z1 – z2 вычитаем действительные и мнимые части чисел z1 и z2: u = z1 – z2 = (2 – j 7) – (3 + j5) = (2–3) + j(–7–5) = –1–j12.
2). Вектор, соответствующий числу z, строим как сумму векторов z1 и z2 по правилу параллелограмма, а вектор, соответствующий числу u, строим как сумму векторов z1 и (– z2).
3). Найдем модуль r и аргумент φ чисел z1 и z2. z1 = 2 – j 7, число принадлежит IVчетверти, значит φ1 = – arctg r1 = z2 = 3 + j5, число принадлежит I четверти, значит φ2 = arctg r2 = Запишем числа z1 и z2 в показательной z = r
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.100 (0.185 с.) |
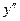 = с,
= с, 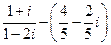 .
.
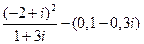 .
.
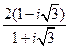 .
.
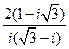 .
.
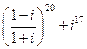 .
.
 .
.
 .
.
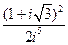 .
.
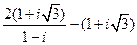 .
.
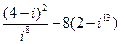 .
.
 (cos 70o + i sin 70o).
(cos 70o + i sin 70o).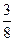 (cos 25o + i sin 25o).
(cos 25o + i sin 25o). .
.
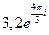
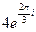
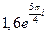
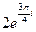
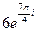
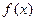 =
= 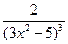 и вычислите
и вычислите 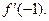
 =
= 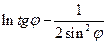 и вычислите
и вычислите 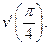
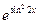 и вычислите
и вычислите 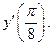
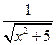 и вычислите
и вычислите 
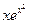 и вычислите
и вычислите 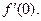
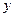 =
= 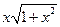 и вычислите
и вычислите 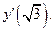
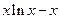 и вычислите
и вычислите 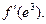
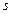 =
= 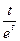 и вычислите
и вычислите 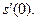

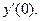
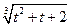 и вычислите
и вычислите  =
=  и вычислите
и вычислите 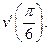
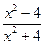 и вычислите
и вычислите 
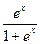 и вычислите
и вычислите 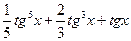 и вычислите
и вычислите 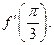
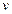 =
= 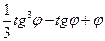 и вычислите
и вычислите  и вычислите
и вычислите 
 и вычислите
и вычислите 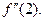
 и вычислите
и вычислите 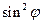 и вычислите
и вычислите 
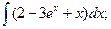
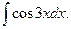

 .
.
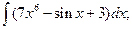
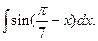


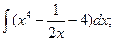
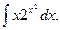
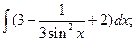
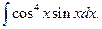
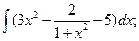
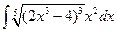


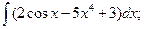

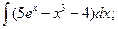

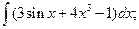

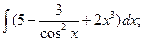
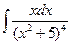
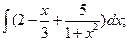
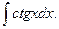

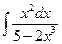
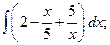
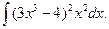
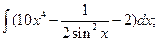
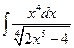

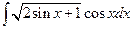
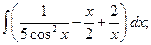
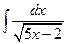
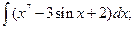
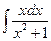
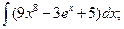
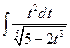
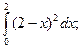
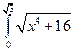 х 3 dx.
х 3 dx.
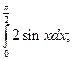
 .
.
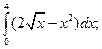
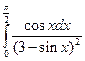 .
.

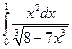 .
.
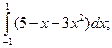
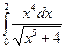 .
.

 dx.
dx.

 dx.
dx.
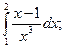
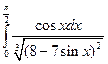 .
.
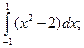
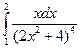 .
.
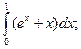
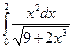 .
.
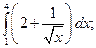
 dx.
dx.
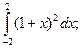
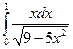 .
.
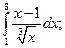
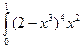 dx.
dx.
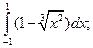
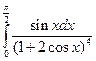 .
.

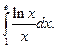 .
.
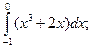
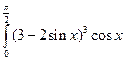 dx.
dx.

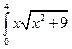 dx.
dx.

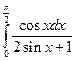 .
.
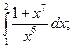
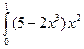 dx.
dx.

 dx.
dx.
 5.11.
5.11.
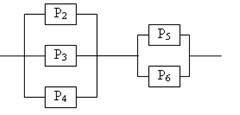



 5.20.
5.20.

 Ось Х – действительная ось, соответствует
Ось Х – действительная ось, соответствует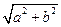
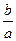 ׀
׀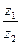 =
= 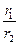 (cos(φ1- φ 2)+ j sin(φ1- φ 2))
(cos(φ1- φ 2)+ j sin(φ1- φ 2))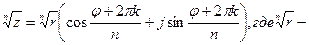 арифметический корень, k=0, 1, 2, …,n-1.
арифметический корень, k=0, 1, 2, …,n-1.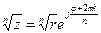 k=0, 1, 2, …,n-1.
k=0, 1, 2, …,n-1.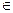 (a;b) дадим приращение
(a;b) дадим приращение 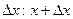
 ;
;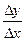 ;
;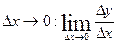 .
.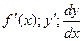 .
.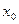 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.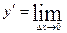
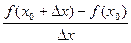 или
или  =
= 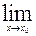
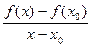 .
.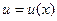 и
и 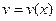 - две дифференцируемые в некотором интервале (a;b) функции. Тогда: 1.
- две дифференцируемые в некотором интервале (a;b) функции. Тогда: 1. 

 где с = const;
где с = const;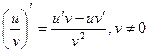 .
.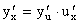 .
.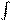 f(x)dx:
f(x)dx: 
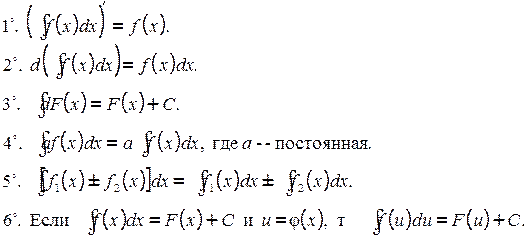
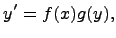
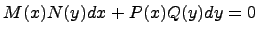
 и
и 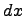 , в другую часть уравнения - только функции от y и dy. Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:
, в другую часть уравнения - только функции от y и dy. Затем в полученном дифференциальном уравнении надо проинтегрировать обе части: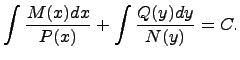
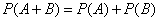
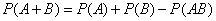
 , где
, где 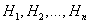 - полная группа гипотез, то есть
- полная группа гипотез, то есть 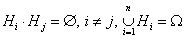 ,
,  - достоверное событие.
- достоверное событие.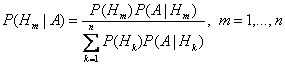 , где
, где 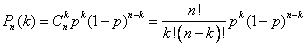 - вероятность появления события ровно
- вероятность появления события ровно 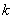 раз при
раз при  независимых испытаниях,
независимых испытаниях, 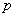 - вероятность появления события при одном испытании.
- вероятность появления события при одном испытании.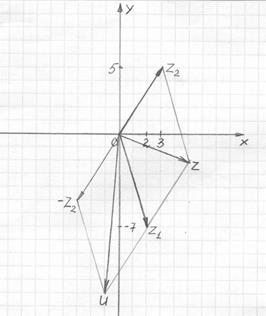
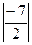 = – arctg3,5
= – arctg3,5 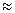 – 74,05°.
– 74,05°. =
=  .
.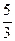
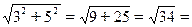 5,83.
5,83.


