
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь криволинейной трапеции.⇐ ПредыдущаяСтр 38 из 38
Пусть на сегменте Фигуру, ограниченную линиями
Доказательство. Возьмём произвольное разбиение сегмента
Естественно полагать, что площадь ступенчатой фигуры стремится к площади криволинейной трапеции при стремлении к нулю наибольшей длины
Равенство (1) доказано. Замечание. В случае, когда график функции
Площадь криволинейного сектора. Пусть кривая Докажем, что для площади
Доказательство. Рассмотрим произвольное разбиение сегмента
Интегральная сумма (7) равна площади веерообразной фигуры, состоящей из круговых секторов радиуса
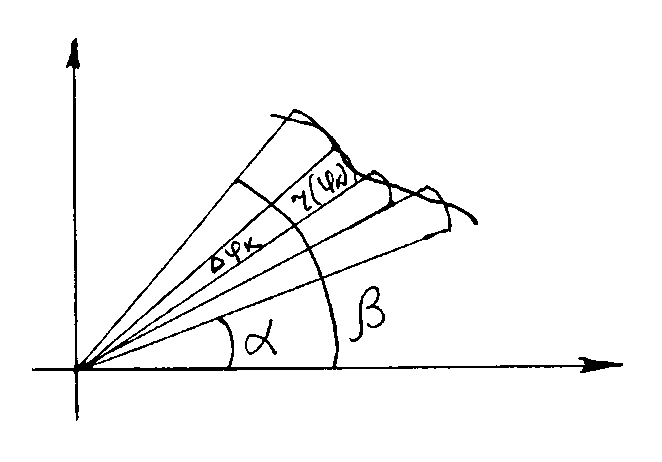
Так как площадь криволинейного сектора
Справедливость формулы (6) доказана. Длина дуги плоской кривой. Пусть в плоскости
Определение 6.1. Кривая
Предположим, что кривая Справедливо следующее утверждение: если функция
Доказательство. Возьмём произвольное разбиение отрезка
Пользуясь формулой Лагранжа
следовательно
Тогда длина вписанной ломаной равна
Правая часть равенства (10) представляет собой интегральную сумму непрерывной на сегменте Пользуясь тем, что при стремлении к нулю
Тем самым утверждение доказано. Замечание. Рассмотрим случай, когда кривая
Т.е.
Замечание 2. Пусть теперь кривая
Тогда
4. Объём тела вращения. Пусть на сегменте
Доказательство. Рассмотрим произвольное разбиение сегмента
В каждом частичном сегменте
На каждом частичном сегменте
Сумма объёмов всех
C другой стороны сумма в правой части равенства (13) представляет собой интегральную сумму функции
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.75.227 (0.017 с.) |
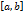 задана неотрицательная и непрерывна функция
задана неотрицательная и непрерывна функция  .
. , отрезком
, отрезком  и графиком функции
и графиком функции 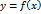 назовём криволинейной трапецией. Площадь указанной криволинейной трапеции обозначим через
назовём криволинейной трапецией. Площадь указанной криволинейной трапеции обозначим через  .
.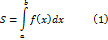

 . Выберем на каждом частичном сегменте
. Выберем на каждом частичном сегменте 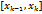 произвольную точку
произвольную точку  . Для данного разбиения и данного выбора точек
. Для данного разбиения и данного выбора точек 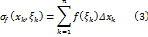
 Интегральная сумма (3) равна площади ступенчатой фигуры, указанной на рис. 1. Так как, площадь
Интегральная сумма (3) равна площади ступенчатой фигуры, указанной на рис. 1. Так как, площадь 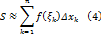
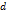 частичных сегментов разбиения (2). Таким образом
частичных сегментов разбиения (2). Таким образом
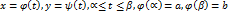 , получим
, получим
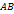 задана в полярных координатах уравнением
задана в полярных координатах уравнением  , где
, где  - неотрицательная и непрерывная на сегменте
- неотрицательная и непрерывная на сегменте 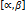 функция. Плоскую фигуру, ограниченную кривой
функция. Плоскую фигуру, ограниченную кривой 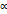 и
и  , будем называть криволинейным сектором.
, будем называть криволинейным сектором.

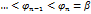 и выберем в каждом частичном сегменте
и выберем в каждом частичном сегменте 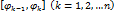 произвольную точку
произвольную точку  , отвечающую данному разбиению и данному выбору точек
, отвечающую данному разбиению и данному выбору точек 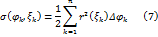
 .
.
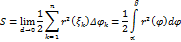
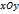 дана некоторая кривая
дана некоторая кривая 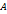 к
к 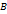 возьмём точки
возьмём точки . Соединив последовательно взятые на кривой
. Соединив последовательно взятые на кривой 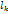 длину звена
длину звена 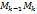 указанной ломаной, а через
указанной ломаной, а через  - длину наибольшего из её звеньев
- длину наибольшего из её звеньев 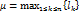 .
. , к которому стремится длина вписанной в эту кривую ломаной при стремлении к нулю её наибольшего звена. При этом указанный предел
, к которому стремится длина вписанной в эту кривую ломаной при стремлении к нулю её наибольшего звена. При этом указанный предел  , непрерывную на сегменте
, непрерывную на сегменте 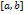 , то длина
, то длина 

 и рассмотрим точки
и рассмотрим точки 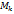 кривой
кривой 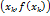 , тогда точки
, тогда точки  определяют некоторую, в писанную в кривую
определяют некоторую, в писанную в кривую 



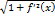 , отвечающей разбиению (9) и некоторому выбору точек
, отвечающей разбиению (9) и некоторому выбору точек 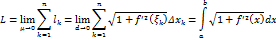

 , при этом
, при этом  , где функции
, где функции 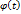 и
и 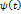 имеют непрерывные производные
имеют непрерывные производные  и
и  на
на 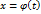 и, учитывая, что
и, учитывая, что  , из формулы (8) получим
, из формулы (8) получим

 имеет непрерывную на
имеет непрерывную на  , при этом радиус-векторы
, при этом радиус-векторы 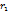 и
и  точек
точек  . В этом случае, переходя к прямоугольным координатам
. В этом случае, переходя к прямоугольным координатам 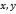 , получим параметрические уравнения кривой
, получим параметрические уравнения кривой 
 . Пользуясь формулой (10), найдём
. Пользуясь формулой (10), найдём


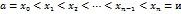
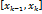 возьмём точку
возьмём точку 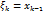 .
.
 . При вращении вокруг оси
. При вращении вокруг оси  , где
, где  .
. цилиндров приближённо равна объёму данного тела вращения
цилиндров приближённо равна объёму данного тела вращения
 на сегменте
на сегменте  непрерывна, то предел этой суммы при стремлении к нулю
непрерывна, то предел этой суммы при стремлении к нулю  . Следовательно, объём тела вращения криволинейной трапеции вокруг оси
. Следовательно, объём тела вращения криволинейной трапеции вокруг оси 



