
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Существование первообразной у любой непрерывной функции.
В данном параграфе мы будем рассматривать интеграл вида
определённую в каждой точке Справедлива следующая теорема 3.1. Пусть функция
Доказательство. По определению производной функции
Согласно формуле среднего значения
Учитывая равенство (4) в равенстве (3), получим
Пользуясь непрерывностью функции Замечание. В теореме 1.1 мы доказали, что Основная формула интегрального исчисления. Формула Ньютона-Лейбница. Пусть функция
является одной из первообразных функции Теорема 4.1. Пусть функция
Доказательство. Т.к.
Тем самым справедливость формулы (1) доказана. Формула (1) называется формулой Ньютона-Лейбница. Пользуясь обозначением
формулу Ньютона-Лейбница можно записать в виде
Замена переменной в определённом интеграле. Теорема 4.2. Пусть функция
Доказательство. Пусть
Рассмотрим функцию
Следовательно функция
Согласно формуле (5), правая часть последнего равенства равна
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.183.89 (0.007 с.) |
 , где подынтегральная функция
, где подынтегральная функция 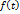 определена и интегрируема на некотором сегменте
определена и интегрируема на некотором сегменте 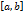 , а
, а  - произвольная точка сегмента
- произвольная точка сегмента 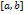 , т.е.
, т.е. 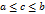 . В указанных предположениях мы можем рассмотреть функцию
. В указанных предположениях мы можем рассмотреть функцию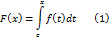
 сегмента
сегмента  непрерывна на сегменте
непрерывна на сегменте 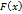 , определённая равенством (1) дифференцируема в каждой точке
, определённая равенством (1) дифференцируема в каждой точке 
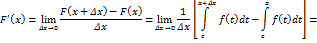
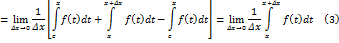
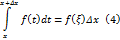 где
где 
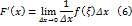
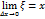 , из равенства (6) получим
, из равенства (6) получим 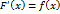 . Теорема 1.1 доказана.
. Теорема 1.1 доказана.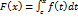 является одной из первообразных непрерывной на сегменте
является одной из первообразных непрерывной на сегменте 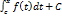 .
.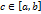 , функция
, функция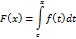
 , получим, что и функция
, получим, что и функция 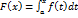 является первообразной функции
является первообразной функции 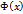 - любая первообразная функции
- любая первообразная функции 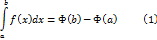
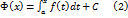 , где
, где 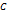 - некоторая постоянная. Пользуясь равенством (2), вычислим
- некоторая постоянная. Пользуясь равенством (2), вычислим 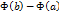 .
.
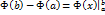
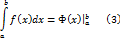
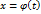 дифференцируема на сегменте
дифференцируема на сегменте 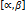 , причём производная
, причём производная  непрерывна в каждой точке сегмента
непрерывна в каждой точке сегмента 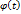 является сегмент
является сегмент 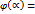
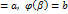 , тогда справедлива следующая формула
, тогда справедлива следующая формула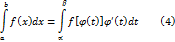

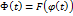 , определённую на сегменте
, определённую на сегменте 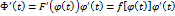
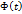 является первообразной для непрерывной на сегменте
является первообразной для непрерывной на сегменте 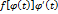 , поэтому согласно формуле Ньютона-Лейбница
, поэтому согласно формуле Ньютона-Лейбница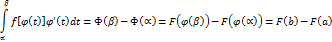
 . Следовательно справедливость формулы (4) и теоремы 4.2 доказана.
. Следовательно справедливость формулы (4) и теоремы 4.2 доказана.


