
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки перегиба графика функции.
Пусть функция Определение 5.2. Точка
На рисунке изображён график функции, имеющей перегиб в точке Теорема 5.3. (Необходимое условие перегиба графика функции). Если график функции Доказательство. Предположим обратное, т.е. Теорема 5.4. (Первое достаточное условие перегиба) Пусть функция Доказательство. Т.к. вторая производная Теорема 5.5. (Второе достаточное условие перегиба). Если функция Доказательство. Итак
Т.к. По предположению Итак, вторая производная
Асимптоты графика функции. Определение 6.1. Будем говорить, что прямая Пример. График функции
Определение 6.2. Прямая
где Теорема 6.1. Для того, чтобы прямая
Доказательство. Необходимость. Пусть прямая
Рассмотрим теперь предел Достаточность. Пусть выполнены равенства (2). Тогда из существования предела В заключение данного параграфа приведём схему исследования графика функции. Целесообразно провести следующие исследования. 1. Установить область определения функции. 2. Выяснить вопрос о существовании асимптот (вертикальных и наклонных) 3. Найти области возрастания и убывания функции и точки экстремума. 4. Найти области сохранения выпуклости и точки перегиба. 5. Найти точки пересечения графика функции с осями После проведения указанных исследований легко строится эскиз графика функции. Пусть функция Иными словами функция Естественно возникает вопрос: как найти точки глобального максимума и глобального минимума
Приведём описание процесса нахождения глобального максимума
Пусть
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.192 (0.015 с.) |
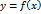 дифференцируема на интервале
дифференцируема на интервале 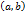 , а
, а  – произвольная точка интервала
– произвольная точка интервала 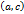 и
и  .
. графика функции
графика функции 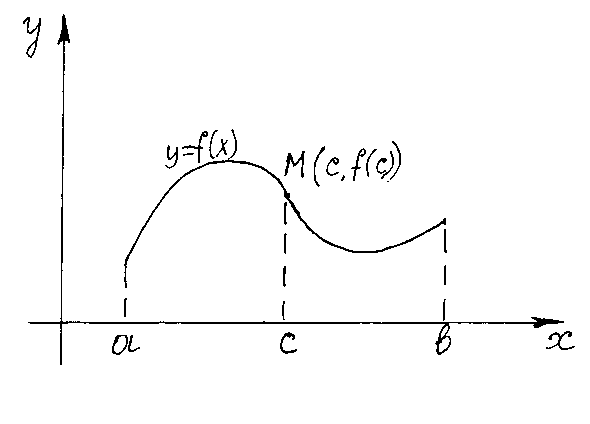
 имеет непрерывную вторую производную в точке
имеет непрерывную вторую производную в точке 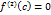 .
.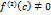 . Тогда
. Тогда  или
или  . Рассмотрим случай
. Рассмотрим случай  имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки  , то график этой функции имеет перегиб в точке
, то график этой функции имеет перегиб в точке 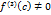 . Для определённости будем считать, что
. Для определённости будем считать, что  . Тогда по определению производной третьего порядка
. Тогда по определению производной третьего порядка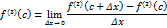

 такое, что для всех
такое, что для всех  , для которых выполнены неравенства
, для которых выполнены неравенства  , справедливо неравенство
, справедливо неравенство  . Пусть
. Пусть 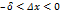 , тогда из неравенства (1) получим
, тогда из неравенства (1) получим  , т.е. вторая производная отрицательна слева от точки
, т.е. вторая производная отрицательна слева от точки  , тогда из неравенства (1) получим
, тогда из неравенства (1) получим  , т.е. вторая производная положительна справа от точки
, т.е. вторая производная положительна справа от точки 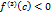 . Теорема 5.5 доказана.
. Теорема 5.5 доказана. является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  или
или  равен
равен 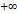 или
или 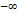 .
. имеет вертикальную асимптоту
имеет вертикальную асимптоту 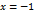 , т.к.
, т.к. 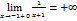 ,
, .
.
 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  , если функция
, если функция 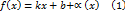
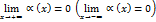 .
.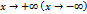 необходимо и достаточно, чтобы выполнялись следующие равенства:
необходимо и достаточно, чтобы выполнялись следующие равенства:

 , где
, где  и перейдём к пределу в полученном равенстве при
и перейдём к пределу в полученном равенстве при 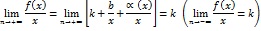


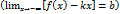 следует, что разность
следует, что разность  является бесконечно малой при
является бесконечно малой при 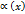 , получим для функции
, получим для функции  и
и  .
.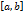 , тогда в силу второй теоремы Вейерштрасса существуют точки
, тогда в силу второй теоремы Вейерштрасса существуют точки 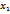 и
и 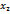 сегмента
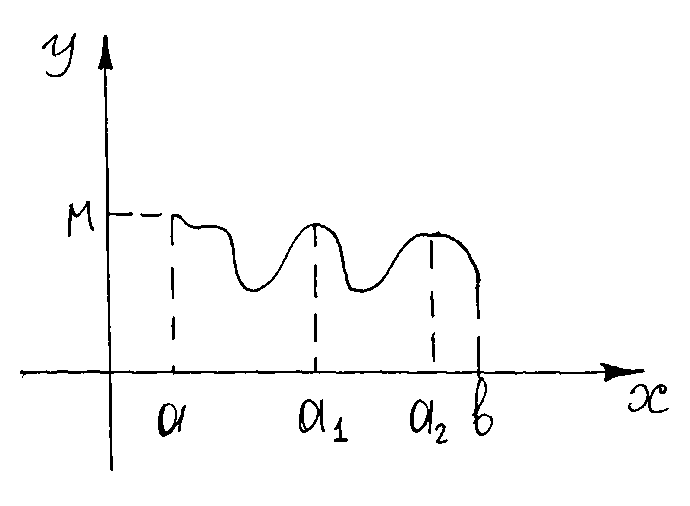
сегмента  .
.
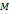 и соответствующей точки
и соответствующей точки  и
и  . Если
. Если 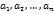 . Тогда число
. Тогда число 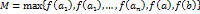 . В качестве точки
. В качестве точки 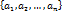 , в которой соответствующее значение функции будет наибольшим. Аналогично находится число
, в которой соответствующее значение функции будет наибольшим. Аналогично находится число 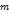 и соответствующая точка
и соответствующая точка 


