
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральная сумма и её предел.
Рассмотрим функцию
Множество точек Составим для заданной функции
называемую интегральной суммой функции Обозначим через Определение 1.1. Число
Определение 1.2. Функция
При этом указанный предел
В этом обозначении функция Из определения следует, что определённый интеграл зависит только от функции
Верхние и нижние суммы. Пусть функция Для произвольного разбиения (1) сегмента
Сумма (3) называется верхней суммой, отвечающей разбиению (1), а сумма (4) – нижней суммой, отвечающей этому разбиению. Справедлива следующая теорема: Теорема 1.1. Для того, чтобы ограниченная на сегменте
где Теорема 1.1 приводится без доказательства. Сформулируем также несколько теорем, доказательства которых приводить не будем. Теорема 1.2. Если функция Теорема 1.3. Если функция Необходимое условие интегрируемости. Теорема 1.4. Если функция Замечание 1. Условие ограниченности функции на сегменте Действительно, рассмотрим функцию
Функция Очевидно, что для любого разбиения сегмента
Итак, Замечание к теореме 1.3. Из интегрируемости функции Действительно, очевидно, что модуль функции Дирихле тождественно равен 1 на сегменте
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.127 (0.008 с.) |
 , определённую на сегменте
, определённую на сегменте 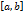 . Пусть
. Пусть  произвольное конечное множество сегмента
произвольное конечное множество сегмента 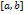 , удовлетворяющее условиям
, удовлетворяющее условиям
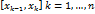 называется
называется 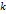 -м частичным сегментом. Длину -го частичного сегмента обозначим через
-м частичным сегментом. Длину -го частичного сегмента обозначим через 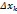 , т.е.
, т.е.  . Пусть
. Пусть  – произвольная точка, принадлежащая
– произвольная точка, принадлежащая 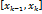
 .
.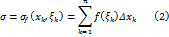
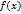 на сегменте
на сегменте 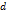 наибольшую длину частичных сегментов данного разбиения сегмента
наибольшую длину частичных сегментов данного разбиения сегмента 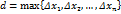 .
.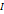 называется пределом интегральных сумм (2) при стремлении к нулю наибольшей длины
называется пределом интегральных сумм (2) при стремлении к нулю наибольшей длины 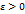 найдётся зависящее от
найдётся зависящее от  положительное число
положительное число 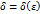 такое, что для всех разбиений сегмента
такое, что для всех разбиений сегмента 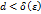 следует неравенство
следует неравенство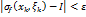

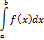
 – нижним пределом интегрирования, а число
– нижним пределом интегрирования, а число  – верхним пределом интегрирования.
– верхним пределом интегрирования.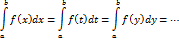
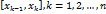 . Обозначим через
. Обозначим через 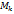 и
и  соответственно точную верхнюю и точную нижнюю грани функции
соответственно точную верхнюю и точную нижнюю грани функции 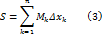

 , такое, что для любого разбиения сегмента
, такое, что для любого разбиения сегмента 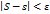
 и
и  – верхняя и нижняя суммы, указанные в равенстве (3) и (4).
– верхняя и нижняя суммы, указанные в равенстве (3) и (4).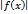 .
.

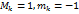 . Поэтому
. Поэтому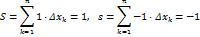
 , тогда из теоремы 1.1 мы заключаем, что функция Дирихле не интегрируема на сегменте
, тогда из теоремы 1.1 мы заключаем, что функция Дирихле не интегрируема на сегменте 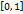 .
.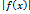 интегрируема на сегменте
интегрируема на сегменте 


