
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцируемость обратной функции.
Теорема 2.2. Пусть функция
Доказательство. Т.к. функция Придадим аргументу
Перейдём к пределу в равенстве (7) при
Заметим, что в силу непрерывности обратной функции Для завершения доказательства теоремы 2.2 остаётся убедиться в том, что предел в правой части равенства (7) существует при Т.к.
Из этого равенства находим
Теорема доказана. 3. Инвариантность формы первого дифференциала. Ниже будет доказано, что установленная в пункте 7 §1 главы 6 формула (10) Пусть аргумент
По правилу дифференцирования сложной функции находим
Подставляя равенство (10) в первое из равенств (9), получим
Инвариантность формы первого дифференциала Замечание. Из универсальности представления (11) вытекает другая, эквивалентная формулировка свойства инвариантности формы первого дифференциала: производная дифференцируемой функции Отношение
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.14.63 (0.005 с.) |
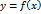 возрастает (убывает) и непрерывна в некоторой окрестности точки
возрастает (убывает) и непрерывна в некоторой окрестности точки  . Пусть, кроме того, эта функция дифференцируема в указанной точке
. Пусть, кроме того, эта функция дифференцируема в указанной точке  в этой точке отлична от нуля. Тогда в некоторой окрестности точки
в этой точке отлична от нуля. Тогда в некоторой окрестности точки  определена обратная для функции
определена обратная для функции 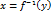 , причём указанная обратная функция дифференцируема в точке
, причём указанная обратная функция дифференцируема в точке 
 обратной функции
обратной функции 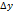 . Этому приращению соответствует приращение
. Этому приращению соответствует приращение 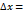
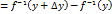 обратной функции в соответствующей точке
обратной функции в соответствующей точке  . Тогда мы можем записать
. Тогда мы можем записать
 .
.
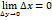 , т.е.
, т.е. 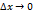 при
при 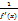 .
.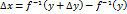 , то
, то  по определению обратной функции. Следовательно
по определению обратной функции. Следовательно  . Учитывая последнее равенство в равенстве (7), получим
. Учитывая последнее равенство в равенстве (7), получим
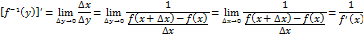
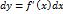 остаётся справедливым и в случае, когда аргумент
остаётся справедливым и в случае, когда аргумент 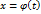 некоторой независимой переменной
некоторой независимой переменной  . Это свойство дифференциала функции называется свойством инвариантности формы первого дифференциала.
. Это свойство дифференциала функции называется свойством инвариантности формы первого дифференциала.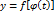 аргумента
аргумента 

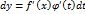 . Учитывая в последнем равенстве второе из равенств (9), получим для дифференциала
. Учитывая в последнем равенстве второе из равенств (9), получим для дифференциала 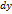 выражение
выражение 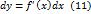 .
.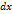 , т.е.
, т.е. 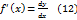 как в случае, когда аргумент
как в случае, когда аргумент  , стоящее в правой части равенства (12) может быть использовано для обозначения производной функции
, стоящее в правой части равенства (12) может быть использовано для обозначения производной функции 


