Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметические операции над непрерывными функциями.
Теорема 5.1. Пусть функции
Доказательство. Так как функции
Примеры непрерывных функций. Непрерывность рациональных функций. Непосредственно из определения, следует непрерывность постоянной функции Функция
Дробно-рациональная функция, т.е. функция вида Например, функция Непрерывность тригонометрических функций.
Докажем, что Из непрерывности функций Непрерывность функции
Итак, пределы функции Функция Замечание. В определении 5.2 интервал Функция
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.151.158 (0.007 с.) |
 и
и 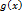 непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 
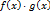 и
и  , также непрерывны в точке
, также непрерывны в точке  ,
,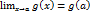 . Тогда
. Тогда  , что доказывает непрерывность функции
, что доказывает непрерывность функции  в точке
в точке 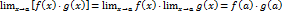 , т.е. функция
, т.е. функция  непрерывна в точке
непрерывна в точке  , т.е. функция
, т.е. функция 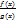 непрерывна в точке
непрерывна в точке 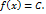 Действительно, в каждой точке
Действительно, в каждой точке 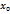 числовой прямой выполняются равенства
числовой прямой выполняются равенства  . Следовательно, постоянная функция непрерывна в каждой точке
. Следовательно, постоянная функция непрерывна в каждой точке 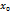 вещественной прямой.
вещественной прямой. также является непрерывной в каждой точке числовой прямой. Действительно
также является непрерывной в каждой точке числовой прямой. Действительно 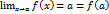 , что означает непрерывность функции
, что означает непрерывность функции 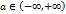 . Из непрерывности функции
. Из непрерывности функции  ,
,  , где
, где  . Из сказанного выше следует непрерывность функции
. Из сказанного выше следует непрерывность функции в любой точке
в любой точке  – любые числа, а
– любые числа, а  , где
, где 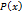 и
и 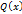 - алгебраические многочлены, непрерывна во всех точках
- алгебраические многочлены, непрерывна во всех точках  , в которых функция
, в которых функция  непрерывна во всех точках, за исключением тех точек, где
непрерывна во всех точках, за исключением тех точек, где  , т.е.
, т.е. 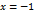 .
. . Покажем, что функция
. Покажем, что функция 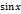 непрерывна в каждой точке
непрерывна в каждой точке 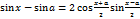 тогда
тогда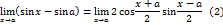
 . Действительно, обозначим
. Действительно, обозначим 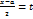 . Очевидно, что
. Очевидно, что 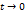 при
при 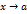 . Тогда
. Тогда 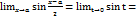 .
.  . Т.е. функция
. Т.е. функция  - бесконечно малая функция при
- бесконечно малая функция при 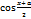 – ограничена
– ограничена 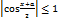 , то из теоремы 4.4. следует, что правая часть равенства (2) равна 0. А это означает, что
, то из теоремы 4.4. следует, что правая часть равенства (2) равна 0. А это означает, что 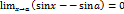 , т.е.
, т.е. 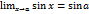 . Непрерывность функции
. Непрерывность функции 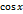 доказывается аналогично.
доказывается аналогично.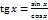 и
и 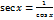 во всех точках, где
во всех точках, где  , т.е. во всех точках, кроме
, т.е. во всех точках, кроме  и функций
и функций  и
и 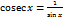 во всех точках, кроме
во всех точках, кроме 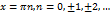
 . Эта функция определена и непрерывна во всех точках числовой прямой. Действительно, в точках интервала
. Эта функция определена и непрерывна во всех точках числовой прямой. Действительно, в точках интервала 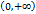 она непрерывна, так как при
она непрерывна, так как при 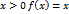 . В точках интервала
. В точках интервала  функция
функция  , эта функция непрерывна как произведение двух непрерывных функций
, эта функция непрерывна как произведение двух непрерывных функций 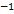 и
и  в точке
в точке  . Для этого вычислим односторонние пределы в точке
. Для этого вычислим односторонние пределы в точке 
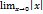 и этот предел равен односторонним пределам, т.е. нулю. Следовательно для функции
и этот предел равен односторонним пределам, т.е. нулю. Следовательно для функции 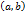 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке  ,
,  ,
,  .
.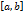 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке  слева, т.е.
слева, т.е.