
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность простейших элементарных функций.
Простейшими элементарными функциями обычно называют следующие функции:
Представление об этих функциях и об их графиках читатель имеет из курса элементарной математики. Наша основная задача – выяснение вопроса об непрерывности всех простейших элементарных функций во всех точках областей их определения. Строгое математическое выяснение этих вопросов не является простым и выходит за рамки настоящего курса. Поэтому мы вынуждены будем приводить некоторые утверждения без доказательства. 1. Показательная функция
2. Логарифмическая функция. Так как на произвольном сегменте
Поскольку левый конец Графики логарифмической функции для
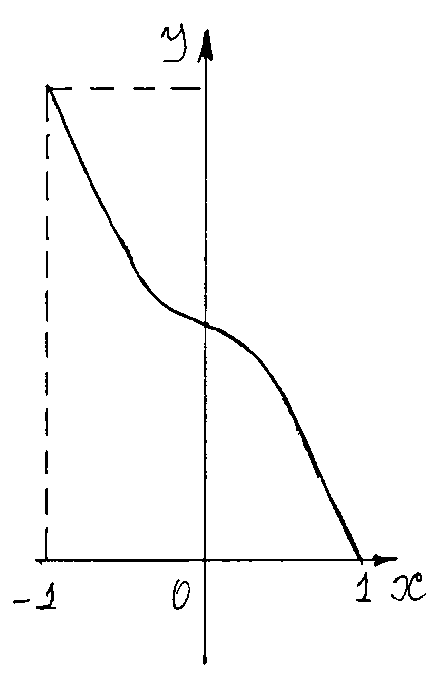
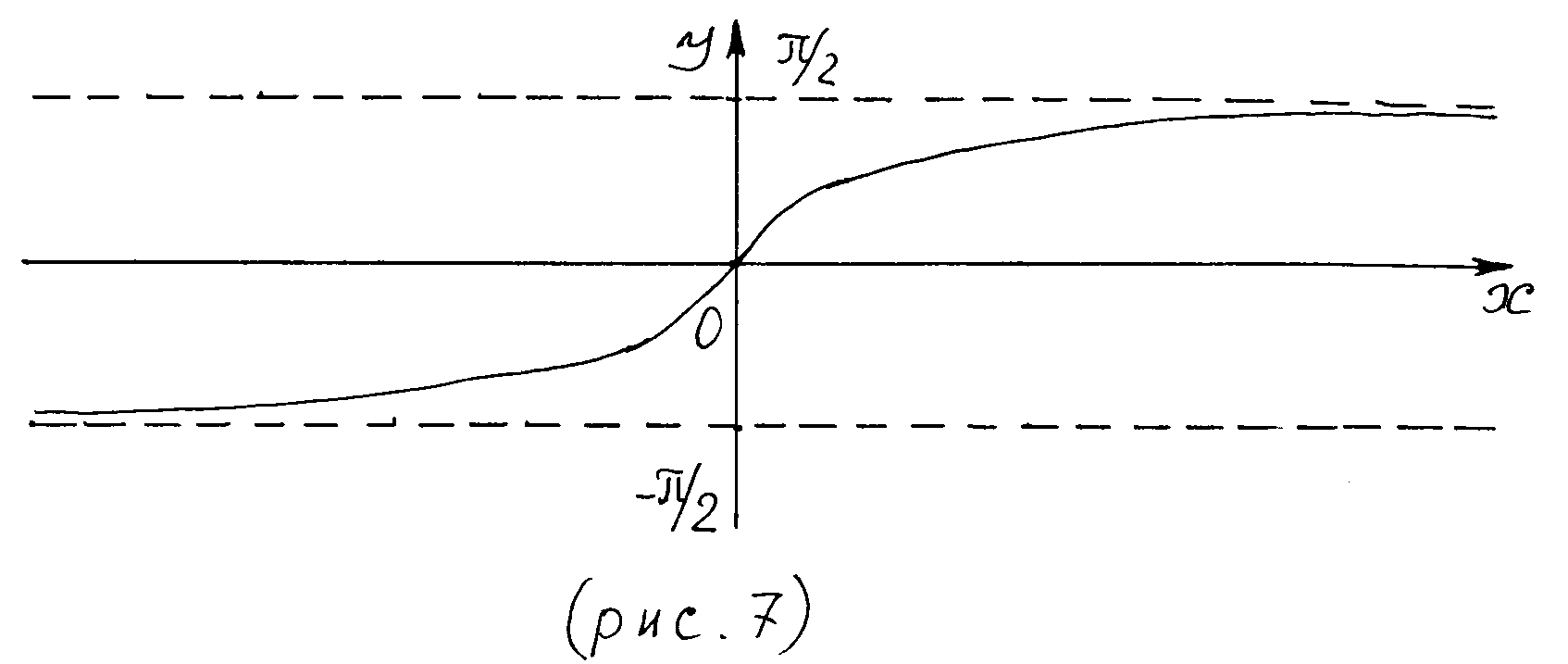
3. Обратные тригонометрические функции. Так как функция Аналогично устанавливается, что функция
Функция Графики обратных тригонометрических функций изображены на рис. 5 – 8.
4. Степенная функция. Пусть Пользуясь основным логарифмическим тожеством
т.е. как сложную функцию вида Так как
Далее, из того, что функция На рис. 9 изображены графики функции
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.197 (0.01 с.) |
 (где
(где 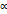 - постоянное вещественное число),
- постоянное вещественное число), 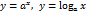 (где
(где 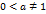 ),
), 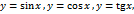
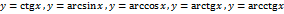 .
.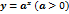 непрерывна в каждой
непрерывна в каждой  точке
точке  бесконечной прямой
бесконечной прямой 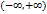 . При этом функция
. При этом функция 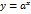 возрастает при
возрастает при 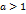 и убывает при
и убывает при 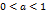 . Областью изменения функции
. Областью изменения функции 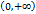 . Графики функции
. Графики функции 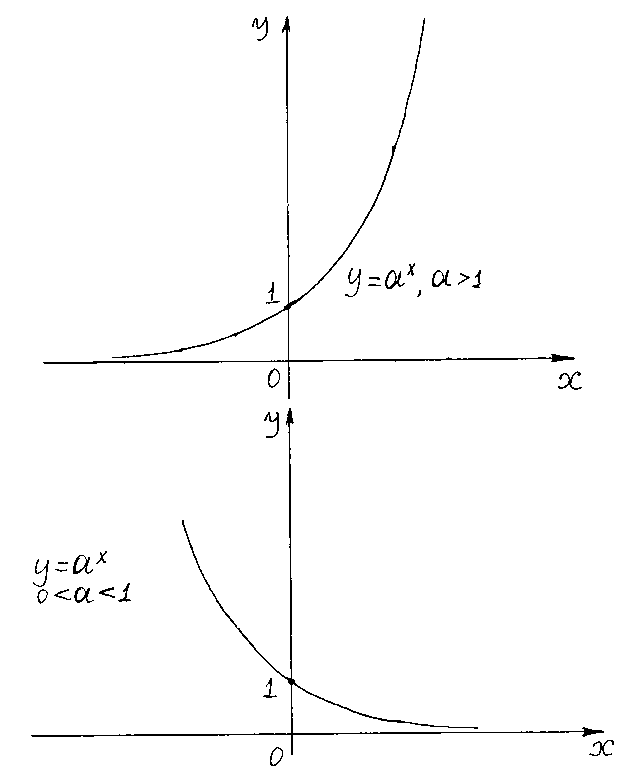
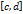 бесконечной прямой
бесконечной прямой 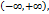 функция
функция  непрерывна и возрастает при
непрерывна и возрастает при  при
при 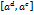 при
при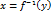 , которая непрерывна и возрастает на сегменте
, которая непрерывна и возрастает на сегменте 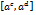 при
при 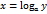 .
. мы можем неограниченно приближать к
мы можем неограниченно приближать к 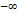 , а правый конец
, а правый конец 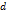 неограниченно приближать к
неограниченно приближать к 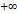 , то в силу равенств
, то в силу равенств 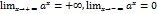 , справедливых при
, справедливых при  и будет на этой полупрямой возрастать при
и будет на этой полупрямой возрастать при  на
на  , которая определена и непрерывна на открытой полупрямой
, которая определена и непрерывна на открытой полупрямой  и на этой полупрямой возрастает при
и на этой полупрямой возрастает при 

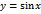 непрерывна и возрастает на сегменте
непрерывна и возрастает на сегменте  и имеет множеством своих значений сегмент
и имеет множеством своих значений сегмент 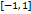 , то в силу теоремы 4.7 на сегменте
, то в силу теоремы 4.7 на сегменте 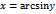 , которая непрерывна и возрастает на этом сегменте. Меняя для этой функции обозначение аргумента
, которая непрерывна и возрастает на этом сегменте. Меняя для этой функции обозначение аргумента  , непрерывной и возрастающей на сегменте
, непрерывной и возрастающей на сегменте  , обратная к непрерывной и убывающей на сегменте
, обратная к непрерывной и убывающей на сегменте  функции
функции 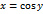 , является непрерывной и убывающей на сегменте
, является непрерывной и убывающей на сегменте 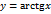 , обратная к непрерывной и возрастающей на интервале
, обратная к непрерывной и возрастающей на интервале 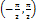 функции
функции 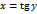 , является непрерывной и возрастающей на бесконечной прямой
, является непрерывной и возрастающей на бесконечной прямой 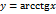 , обратная и непрерывная к непрерывной и убывающей на интервале
, обратная и непрерывная к непрерывной и убывающей на интервале  функции
функции 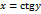 , является непрерывной и убывающей на бесконечной прямой
, является непрерывной и убывающей на бесконечной прямой 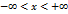 .
.
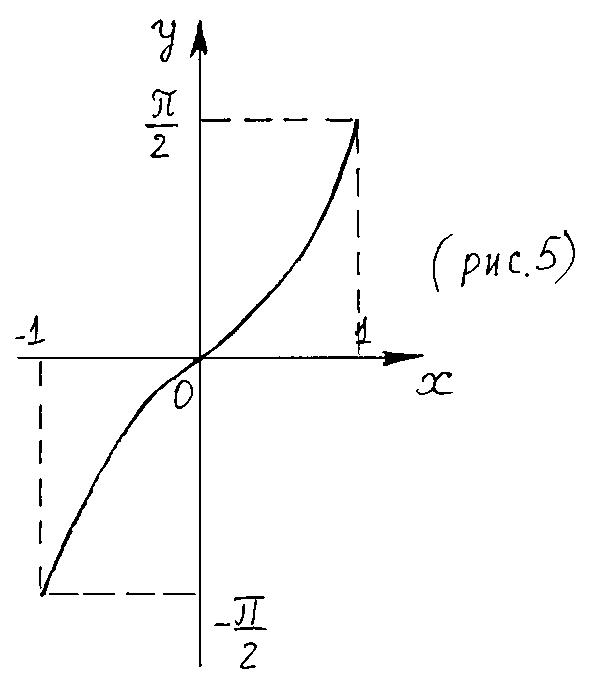

 - некоторое вещественное число, большее единицы.
- некоторое вещественное число, большее единицы.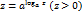 , представим степенную функцию
, представим степенную функцию 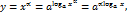
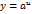 , где
, где 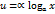 .
. возрастает на полупрямой
возрастает на полупрямой  и убывает при
и убывает при 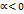 на этой полупрямой. Отсюда и из того, что функция
на этой полупрямой. Отсюда и из того, что функция 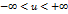 вытекает, что степенная функция
вытекает, что степенная функция  бесконечной прямой
бесконечной прямой 



