
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия возрастания и убывания (монотонности) функции.
· если производная функции y=f(x) положительна для любого x из интервала (a,b), то функция возрастает на (a,b); · если производная функции y=f(x) отрицательна для любого x из интервала (a,b), то функция убывает на (a,b). · Если производная функции у=f (x) равна нулю для любого х из интервала (а,b), то функция постоянная на (a,b) Доказательство: Доказывается достаточный признак монотонности на основании теоремы Лагранжа: Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале существует хотя бы одна точка x=с, такая, что f(b)−f(a)=f′(с)(b−a). Далее Е – принадлежит, V - любые v Выберем производную m x1,x2E(a,b), пусть х1<х2. На интервале (а,b) ф-ия у=f(x) удвл. усл. теоремы Лагранжа, поэтому применим в виде: f(x2)-f(x1)=f' (c)(x2-x1) 1)Пусть f(x)>0 VxE(a,b), в частности f'(c)>0, т.к. m.CE(x1;x2) c(a;b) f(x2)-f(x1)=f' (c)(+) (x2-x1)(+) >0 -> f(x2)-f(x1)>0 -> f(x1)<f(x2) и x2>x1 по опр.возр.ф. -> y=f(x) возрастает на интервале (a;b) 2) Пусть f'(x)<0 VxE(a,b) в частности f'(c)<0,т.к. cE(a,b) f(x2)-f(x1)=f'(c)(-) (x2-x1)(+) < 0 -> f(x2)-f(x1)<0 -> f(x2)<f(x1) ->x2 <x1 по опр.убыв.ф. -> y=f(x) убывает на интервале (a,b) 3) f'x)=0 VxE(a,b), в частности f'(c)=0 f(x2)-f(x1)=f'(c)(=0) (x2-x1)= 0 -> Vx1,x2E(a,b) f(x1)=f(x2) -> y=f(x) = C = const v f(b) - f(a) = f'(c) (b-a)
23. Определение точки минимума и точки максимума y = f (x). Доказательство необходимого признака экстремума функции y = f (x). Доказательство первого достаточного признака экстремума функции y = f (x). Доказательство второго достаточного признака экстремума функции y = f (x). Определение точки минимума: т. х0 принадлежащая области определения функции y=f(x) называется точкой минимума этой функции если для всех точек х Определение точки максимума: т. х0 принадлежащая области определения функции y=f(x) называется точкой максимума этой функции если для всех точек х≠х0 из некоторой окрестности точки х0 выполняется неравенство f(x)<f(x0) Необходимый признак экстремума: если функция y=f(x) имеет экстремум в точке х0, то f’(x0)=0 или f’(x0) не существует Доказательство: пусть х0 – точка максимума, тогда по окр. точки М Рассмотрим · Если · Если Если f’(x0) существует, то
Первый достаточный признак экстремума: пусть функция y=f(x) непрерывна в точке х0 и дифференцируема в некоторой окрестности точки х0 (кроме может быть самой точки х0). Если f’(x) при переходе через х0 меняет знак с «+» на «-», то х0-max, если с «-» на «+», то х0-min.
Доказать: х0- точка max Доказательство: Возьмем произвольную точку а) Рассмотрим [x;x0]. По теореме Лагранжа
т.к. х0-х>0 и по условию f’(c)>0, тогда б) Рассмотрим [x0;x]. По теореме Лагранжа
т.к. по условию f’(c)<0 и х-х0>0, то исходя из а) и б) Доказать: х0- точка min Доказательство: Возьмем произвольную точку а) Рассмотрим [x;x0]. По теореме Лагранжа
т.к. х0-х>0 и по условию f’(c)<0, тогда б) Рассмотрим [x0;x]. По теореме Лагранжа
т.к. по условию f’(c)>0 и х-х0>0, то исходя из а) и б) Второй достаточный признак экстремума: пусть функция y=f(x) непрерывна в точке х0. Точка х0 является точкой экстремума функции y=f(x), если: 1) f’(x0)=0; 2) f’’(x0)≠0, причем а) если f’’(x0)>0, то х0- точка min б) если f’’(x0)<0, то х0- точка max Пусть выполнены условия теоремы и f’’(x)> 0. Тогда f’(x)в Если f’’(x)<0, то f’(x) в
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.148.124 (0.005 с.) |
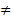 х0 из некоторой окрестности точки х0 выполняется неравенство f(x)>f(x0)
х0 из некоторой окрестности точки х0 выполняется неравенство f(x)>f(x0)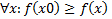 для всех
для всех 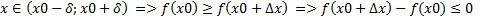
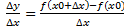
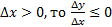
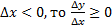
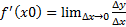
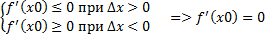
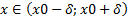
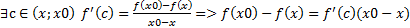
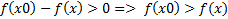
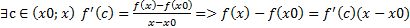

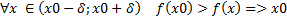 – max
– max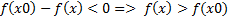
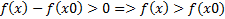
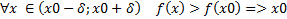 – min
– min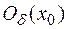 возрастает, но f’(x)= 0, следовательно, в
возрастает, но f’(x)= 0, следовательно, в 


