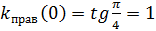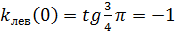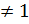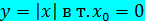Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполним подстановку в исходный предел
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции: 6 y=logaX Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По имеем: Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство
Правила дифференцирования суммы, произведения и частного (с выводом одного из них).
Сумма и разность: Если функции u и v дифференцируемы в точке х0, то их сумма дифференцируема в этой точке: (u+v)' = u' + v'.
Доказательство:
Произведение: Если функции u и v дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке: (uv)' = u'v+uv'. Частное: Если функции u и v дифференцируемы в точке x0 и функция v не равна нулю в этой точке, то частное u/v также дифференцируемо в x0:
Сложная функция. Теорема о производной сложной функции (с доказательством). Пусть дана сложная функция
Теорема: Пусть внутренняя функция
▼ По условию теоремы
т.е.
Рассмотрим
По условию теоремы
Понятие обратной функции. Теорема о дифференцировании взаимно обратных функций (доказательство). Определение Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.
Функция является обратной, если её область значений, есть область определения прямой функции, а область определения, есть область значений прямой функции. {\displaystyle f:X\to Y} Теорема. Пусть функция
Доказательство. · По Фриштер и рисунку: альфа + бетта = pi/2 => бетта = pi/2 – альфа => tg бетта = tg (pi/2 - альфа) = ctg альфа => tg бетта = 1/ tg альфа => => По определению производной
· Из интернетов проклятых: По определению производной
Согласно теореме о непрерывности дифференцируемых функциях,
что влечет за собой доказываемое утверждение.
16: Параметрическое задание функции. Доказательство теоремы о производной функции, заданной параметрически. Производная функции, заданной неявно. Определение: переменная у называется параметрической переменной х, если закон соответствия между переменными задан системой.
Теорема: пусть функция задана параметрически:
Пусть при этом x’(t) Тогда производная функции y’(x)= Доказательство: рассмотрим По условию теоремы при Тогда: Производная высших порядков для функции, заданной параметрически:
Производная от функции, заданной параметрически, является параметрически заданной функцией.
Производная функции, заданной неявно: Функция у называется неявно заданной, если она задана уравнением f(х,у)=0, в котором нельзя выразить ни х, ни у. Порядок дифференцирования неявно заданной функции: 1) Дифференцируем от соотношения F(x,y)=0, считая у функцией от х -(x ( ( 2) В полученном равенстве находим y’=f(x,y) 3) Чтобы найти f’( 17 Связь между существованием производной в точке и непрерывностью функции y=f(x) в этой точке
(с доказательством и примером непрерывной функции, не имеющей производной в некоторой точке.) Если функция имеет производную в точке
Но стоит отметить, что обратное утверждение не верно Пример: А) непрерывность Задаем в точке
Б) Произв.
1б)
2б)
1 Вывод:
d= x -1
Не существует касательной к графику ф-и
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.106 (0.03 с.) |
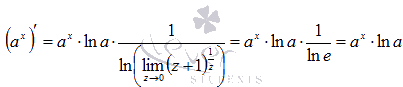

 справедливо в силу второго замечательного предела.
справедливо в силу второго замечательного предела.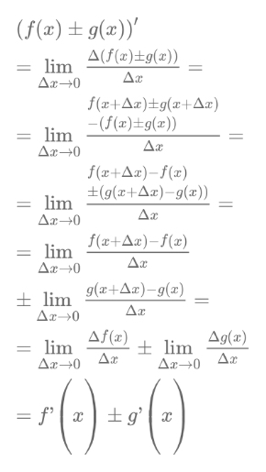

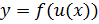 , где
, где  – внешняя функция,
– внешняя функция, – внутренняя функция, область определения которой содержится в области определения внешней функции.
– внутренняя функция, область определения которой содержится в области определения внешней функции. , соответствующую значению
, соответствующую значению 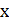 , тогда производная сложной функции
, тогда производная сложной функции  находится по формуле
находится по формуле

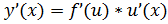 или
или 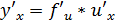
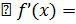 по определению производной =
по определению производной = 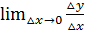 → по теореме о связи функции и ее предела →
→ по теореме о связи функции и ее предела → , где
, где 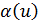 – бесконечно малая при
– бесконечно малая при 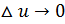 ,
,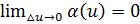
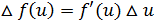 +
+ 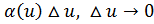
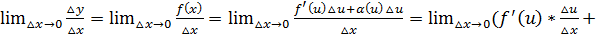
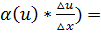 по св-ву предела =
по св-ву предела = 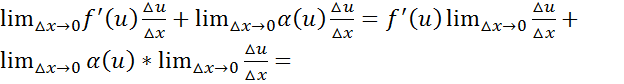 по условию ⱻ
по условию ⱻ 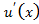
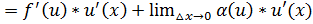
 имеет производную в т. х, следовательно функция
имеет производную в т. х, следовательно функция 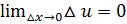 , т.е. при
, т.е. при 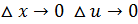 , получим
, получим 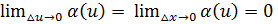
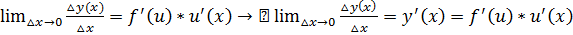 ▼
▼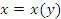 является обратной для функции
является обратной для функции 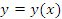 . Если существует отличная от нуля производная функции
. Если существует отличная от нуля производная функции 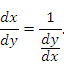
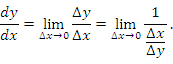
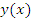 является непрерывной функцией и, следовательно,
является непрерывной функцией и, следовательно, 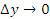 при ∆ x → 0. Тогда
при ∆ x → 0. Тогда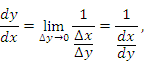
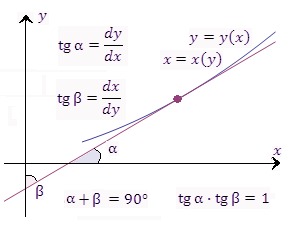
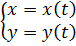
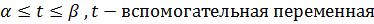
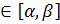 ,
,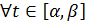
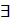 производные функции x(t), y(t),
производные функции x(t), y(t),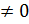
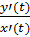
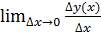 =
= 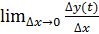
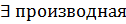 x’(t), то функция x=x(t) непрерывна, значит, по второму определению непрерывности:
x’(t), то функция x=x(t) непрерывна, значит, по второму определению непрерывности: 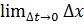 =0, т.е.
=0, т.е.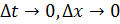
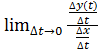 =(по свойству пределов)
=(по свойству пределов) 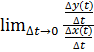 = =
= = 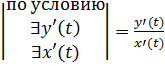 , Ч.Т.Д.
, Ч.Т.Д.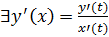 – функция
– функция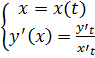
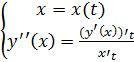
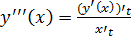 , тогда
, тогда 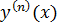 =
= 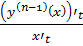
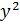 )’=1*
)’=1* 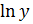 )’=
)’=  *y’(x)
*y’(x)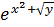 )’=
)’= 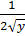 *y’(x))
*y’(x))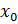 ), надо подставить координаты точки в выражение производной
), надо подставить координаты точки в выражение производной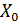 , то она в этой точке непрерывна
, то она в этой точке непрерывна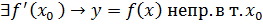 По условию теоремы
По условию теоремы 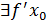 тогда по определению производной
тогда по определению производной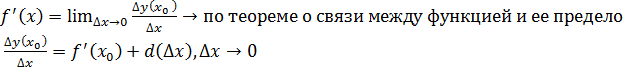
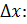
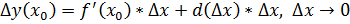
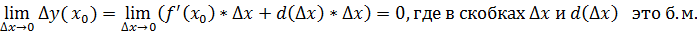
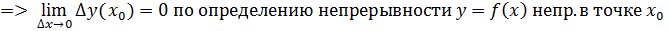
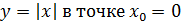
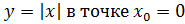
 , тогда
, тогда 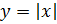 получит приращение
получит приращение 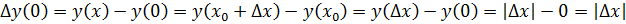
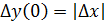
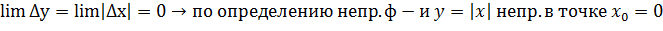
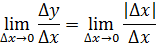
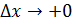
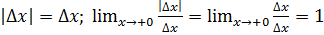
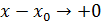
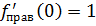
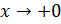
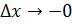
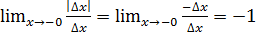
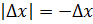
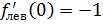
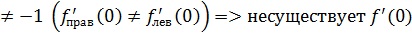
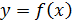 непр. в т.
непр. в т. 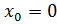 не имеет производной в т.
не имеет производной в т. 
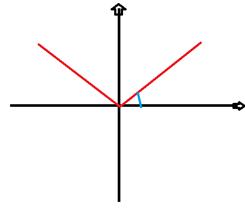 y=-x y y=x
y=-x y y=x