Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экзаменационные билеты к экзамену по высшей математикеСтр 1 из 8Следующая ⇒
Теоремы о пределах: предел суммы, произведения и частного двух функций, имеющих предел (с доказательством одной из теорем) 1) Предел суммы двух функций равен сумме их пределов: Доказательство: Пусть Тогда по теореме о связи функции, её предела и бесконечно малой функции:
По теореме о связи функции, её предела и бесконечно малой функции
2) Предел произведения двух функций равен произведению их пределов: Доказательство: Пусть
Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда 3) Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:
Доказательство: Пусть
По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция. Поэтому Сравнение бесконечно малых. Символ,,о”- малое. Теоремы об эквивалентных бесконечно малых величинах (с доказательством одной из них). Вышмат. Вопрос 6. Сравнение бесконечно малых. Символ,,о”- малое. Теоремы об эквивалентных бесконечно малых величинах (с доказательством одной из них).
Определение: Пусть · Если предел отношения Обозначение: α =о(β) или α << β Читается: a есть «o - малое от b» · Если существует конечный, отличный от нуля, предел их отношений, то бесконечно малые величины a и b называются б.м. одного порядка малости a · Нет необходимости рассматривать случай, когда предел отношения так как в этом случае предел отношения б/а (бета к альфа) равен нулю, значит b является б.м. более высокого порядка, чем a.
· Если же не существует ни конечного, ни бесконечного предела отношения бесконечно малых a и b, то говорят, что эти бесконечно малые не сравнимые по отношению. · Если предел отношения
Эквивалентными бесконечно малыми называются 2 бесконечно малые а и б (альфа и бета) одновременно стремящиеся к 0, предел отношения которых равен 1 Свойства эквивалентных бесконечно малых (теоремы) нулю, были эквивалентны, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка малости, чем любая из них. Доказательство. Доказательство (только для удобства записи) проведем для случая, когда
Необходимость. Дано что Надо доказать. что
Найдем Это значит, что
Достаточность. Дано, что Надо доказать, что
▲Так как
отсюда
2) Предел отношений двух бесконечно малых не изменится, если любую из них заменить на ей эквивалентную. Доказательство. ▲Пусть Дано, что при
Определение Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.
Функция является обратной, если её область значений, есть область определения прямой функции, а область определения, есть область значений прямой функции. {\displaystyle f:X\to Y} Теорема. Пусть функция
Доказательство. · По Фриштер и рисунку: альфа + бетта = pi/2 => бетта = pi/2 – альфа => tg бетта = tg (pi/2 - альфа) = ctg альфа => tg бетта = 1/ tg альфа => => По определению производной
· Из интернетов проклятых: По определению производной
Согласно теореме о непрерывности дифференцируемых функциях,
что влечет за собой доказываемое утверждение.
16: Параметрическое задание функции. Доказательство теоремы о производной функции, заданной параметрически. Производная функции, заданной неявно. Определение: переменная у называется параметрической переменной х, если закон соответствия между переменными задан системой.
Теорема: пусть функция задана параметрически:
Пусть при этом x’(t) Тогда производная функции y’(x)= Доказательство: рассмотрим По условию теоремы при Тогда: Производная высших порядков для функции, заданной параметрически:
Производная от функции, заданной параметрически, является параметрически заданной функцией.
Производная функции, заданной неявно: Функция у называется неявно заданной, если она задана уравнением f(х,у)=0, в котором нельзя выразить ни х, ни у. Порядок дифференцирования неявно заданной функции: 1) Дифференцируем от соотношения F(x,y)=0, считая у функцией от х -(x ( ( 2) В полученном равенстве находим y’=f(x,y) 3) Чтобы найти f’( 17 Связь между существованием производной в точке и непрерывностью функции y=f(x) в этой точке (с доказательством и примером непрерывной функции, не имеющей производной в некоторой точке.) Если функция имеет производную в точке
Но стоит отметить, что обратное утверждение не верно Пример: А) непрерывность Задаем в точке
Б) Произв.
1б)
2б)
1 Вывод:
d= x -1
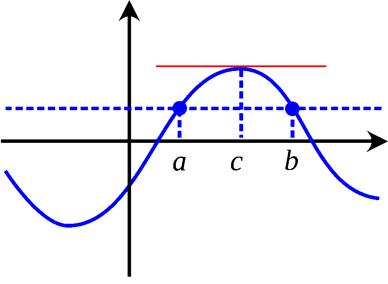
Не существует касательной к графику ф-и Теорема Ролля Теорема. Пусть функция y=f(x) непрерывна на отрезке [a,b], имеет производную f’(x) на интервале (a,b) и при этом f(a)=f(b). Тогда существует точка c ∈ (a,b), в которой выполнено условие f’(c)=0. Доказательство. Функция y=f(x) непрерывна на отрезке [a,b] и, следовательно, достигает на этом отрезке свое наибольшее и наименьшее значение. Если эти значения совпадают, то функция равна константе, и ее производная равна 0 в каждой точке интервала (a,b). Если же наибольшее и наименьшее значения функции не совпадают, то хотя бы одно из них не совпадает со значением функции на границах отрезка. Пусть в точке c ∈ (a,b) достигается наибольшее или наименьшее значение функции на отрезке. Тогда эта точка является точкой экстремума и в этой точке по теореме Ферма производная равна 0. Геометрическая интерпретация. Теорема означает, что если функция y=f(x) удовлетворяет теореме Ролля, то найдется хотя бы одна точка С такая, что касательная к графику функции, проведенная в этой точке, параллельная оси Ox.
Следствие. Если f(a)=f(b)=0, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями непрерывной дифференцируемой функции имеется, хотя бы один, нуль производной.
20. Теорема Коши. Теорема Лагранжа, доказательство, геометрический смысл. Теорема Лагранжа: Если функция Геометрический смысл теоремы Лагранжа: Если в каждой точке дуги кривой существует касательная, то на дуге графика функции
Дано: Доказать: Доказательство: Введем вспомогательную функцию
1. 2. 3.
По теореме Ролля:
Теорема Коши. Теорема Коши (об отношении приращений двух функций). Если функции y = f (x) и y = g(x) 1) непрерывны на отрезке [a;b]; 2) дифференцируемы на интервале (a;b); 3) производная g′(x) ≠ 0 на интервале (a;b). Тогда на интервале (a;b) найдется по крайней мере одна точка x0 такая, что
Из условия теоремы следует, что g′(x) ≠ 0. Это означает, что разность g (b) − g (a) ≠ 0. Действительно, если бы g (b) − g (a) = 0, то функция y = g (x), являясь непрерывной и дифференцируемой, удовлетворяла бы условиям теоремы Ролля и в таком случае g ′(x) была бы равна нулю по крайней мере в одной точке x0 интервала (a; b), что противоречит условию. Введем вспомогательную функцию
Эта функция удовлетворяет всем условиям теоремы Ролля: 1) F(x) непрерывна на отрезке [a;b], так как непрерывны функции у = f (x) и y = g (x); 2) функция F(x) имеет производную всюду в интервале (a;b), поскольку каждое слагаемое в правой части функции F(x) имеет производную на этом интервале; 3) F (a) = F (b) = 0, в чем убеждаемся непосредственной проверкой. Из теоремы Ролля делаем вывод о существовании точки x0, что F ′(x0) = 0. Поэтому Отсюда следует Теорема Лагранжа является частным случаем теоремы Коши: достаточно в теореме Коши взять g(x)=x. Геометрический смысл теоремы Коши Пусть плоская кривая γ описывается параметрическими уравнениями
21. Определение дифференцируемой функции 1. Определение:
Функция Другая формулировка:
Приращение дифференцируемой функции имеет 2 слагаемых 1) 2) 2. Определение: Дифференциал независимой переменной
3. Геометрический смысл дифференциала в точке: Искомая прямая Прямая
22. Определение функции y = f (x), возрастающей (убывающей) в интервале. Доказательство достаточного признака возрастания (убывания) функции на интервале. Доказательство Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым. Возьмем на графике функции y = f(x) произвольную точку M 0 с абсциссой x 0 Î (a; b) и проведем через точку M 0 касательную. Ее уравнение
Итак, уравнение кривой имеет вид y = f(x). Обозначим Разность f(x) – f(x 0) преобразуем по теореме Лагранжа Таким образом,
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа:
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x 0 Î (a; b), а это значит, что кривая выпукла вверх. 25. Определение точки перегиба. Необходимый и достаточный признаки существования точки перегиба графика функции y= f(x) Определение. Рассмотрим функцию y=f(x), которая непрерывна и дифференцируема в точке х0. Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую.
x<x0 x>x0
Доказательство. Дано: х0 – абсцисса точки перегиба функции y=f(x) Поскольку f’’(x) – непрерывна, то по свойству непрерывной функции она сохраняет знак в точке х0 и её окрестности. f ’’(х0)<0 ∀x∈(х0−δ,х0+δ) или f ’’(х0) >0 ∀x∈(х0−δ,х0+δ) В таком случае функция будет либо строго выпукла вверх (при f’’’(x)<0), либо строго выпукла вниз (при f ’’ (x)>0). Но тогда точка х0 не является точкой перегиба, что противоречит условию. Следовательно, предположение неверно и вторая производная в точке перегиба должна быть равна нулю.
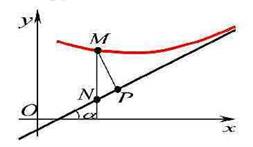
Согласно необходимому условию существования точки перегиба, эти точки находятся среди точек, в которых f ’’(x) равна нулю либо не существует. Точки, в которых f ”(x) равна нулю либо не существует, называются критическими для перегиба (или подозрительными на перегиб), однако не во всякой критической точке будет точка перегиба. Первое достаточное условие существования точки перегиба Если функция f(x) непрерывна и дифференцируема в точке x0, имеет вторую производную f′′(x0) в некоторой проколотой δ-окрестности точки x0 и если вторая производная меняет знак при переходе через точку x0, то x0 является точкой перегиба функции f(x). Доказательство. В таком случае, согласно достаточным условиям выпуклости, функция f(x) выпукла вниз в левой δ-окрестности точки x0 и выпукла вверх в правой δ-окрестности. Следовательно, в точке x0 функция меняет направление выпуклости, т.е. c является, по определению, точкой перегиба. Второе достаточное условие существования точки перегиба 26 Асимптоты графика функции y = f (x). Нахождение вертикальных и наклонных асимптот. Теорема о существовании наклонной асимптоты графика функции (доказательство). Асимптоты графика функции Пусть точка М(x;y) перемещается по графику функции y=f(x), неограниченно удаляясь от начала координат. Если при этом расстояние от т.М до некоторой прямой стремится к 0, то такая прямая- асимптота графика функции y=f(x) . Определение. Прямая L называется асимптотой кривой Г, если расстояние от точки М кривой Г до прямой L стремится к нулю, когда точка М, двигаясь по кривой, бесконечно удаляется от начала координат. Различают два вида асимптот: наклонные и вертикальные. Горизонтальные- частный случай НА. Вертикальная асимптота Вертикальная асимптота- вертикальная прямая, уравнение которой Если функция Верно обратное утверждение: если Вывод: для нахождения вертикальной асимптоты бесконечного разрыва этой функции. Наклонная асимптота НА имеет вид y=kx+b Для того, чтобы график функции y=f(x) имел наклонную асимптоту L: y=kx+b, необходимо и достаточно, чтобы Необходимость Дано: L: y=kx+b – НА графика функции. Доказать: Док-во:
MР перп. L МN перп. 0X MP=
Распишем MN:
MР перп. L МN перп. 0X MP=
Распишем MN:
Достаточность Дано: L: y=kx+b – НА графика функции Доказать:: L: y=kx+b – НА графика функции Док-во: Найдем разность ординат графика функции y=f(x) и прямой L: y=kx+b
Вывод y=kx+b, где Замечание График функции может пересекать наклонную асимптоту, но вертикальную не пересекает.
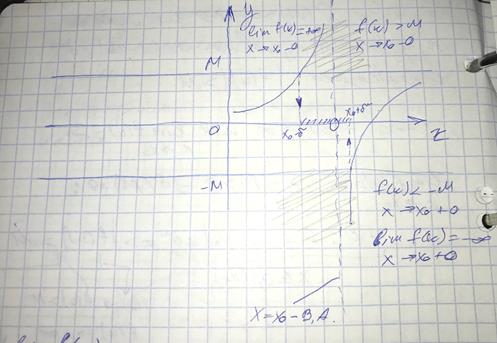
Экзаменационные билеты к экзамену по высшей математике 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 1. Определение предела функции y = f (x) при x Число а называют пределом функции у = f (х) в точке (при x→x0), если для любого сколь угодно малого Е >0, найдется соответствующее нему число δ >0 зависящее от Е, что для всех х≠х0, которые удовлетворяют неравенству 0<|х – х0|<Е, будет выполняться | f (х)-а|< Е. Односторонние пределы функции при х→х0 Геометрический смысл предела функции: 3.Определение бесконечно большой величины при x Функция 𝑦=𝑓(𝑥) называется бесконечно большой при 𝑥→𝑥0, если для любого сколько угодно большого положительного числа 𝑀 существуют такое положительное число 𝛿 (зависящее от 𝑀), что для всех точек 𝑥 из - окрестности точти 𝑥0 будет выполняться неравенство |𝑓(𝑥)|>𝑀. ∀𝑀>0 ∃𝛿=𝛿(𝑀),∀𝑥:0<|𝑥−𝑥0|<𝛿⇒|𝑓(𝑥)|>𝑀
Функция 𝑦=𝑓(𝑥) называется бесконечно большой при 𝑥→∞, если для любого сколько угодно большого положительного числа 𝑀 найдется такое положительное чисто
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.228 с.) |
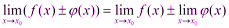
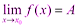 ,
, 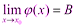
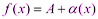

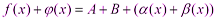 , где
, где 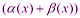 - бесконечно малая функция (по свойству бесконечно малых функций).
- бесконечно малая функция (по свойству бесконечно малых функций).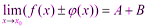 или
или 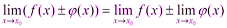

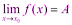 ,
, 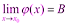 Тогда
Тогда 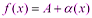 ,
, 
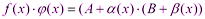

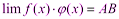 , т.е.
, т.е. 
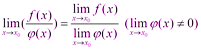
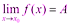 ,
,  Тогда
Тогда 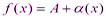 и
и 
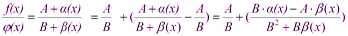
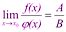 , т.е.
, т.е. 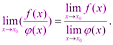
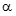 и
и  бесконечно малые величины, одновременно стремящихся к нулю.
бесконечно малые величины, одновременно стремящихся к нулю. равен нулю, то бесконечно малая величина
равен нулю, то бесконечно малая величина 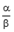 равен бесконечности,
равен бесконечности,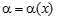 и
и  - функции, являющиеся бесконечно малыми при
- функции, являющиеся бесконечно малыми при 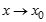 .
. (альфа экв. Бета) при
(альфа экв. Бета) при  (или
(или 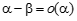 ) при
) при  ▲Обозначим
▲Обозначим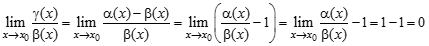 .
.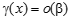 или
или 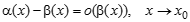 . ▲
. ▲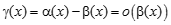 при
при 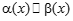 (альфа экв. Бета) при
(альфа экв. Бета) при  , то
, то 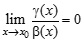 ;
;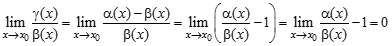 ,
,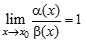 , т. е.
, т. е.  и
и 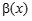 - бесконечно малые функции при
- бесконечно малые функции при 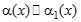 ,
, 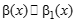 (альфа экв. Альфа 1, бета экв. Бета 1).
(альфа экв. Альфа 1, бета экв. Бета 1).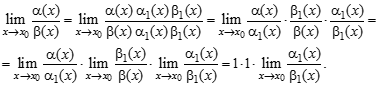
 ▲
▲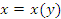 является обратной для функции
является обратной для функции 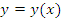 . Если существует отличная от нуля производная функции
. Если существует отличная от нуля производная функции 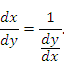
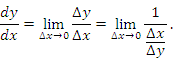
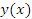 является непрерывной функцией и, следовательно,
является непрерывной функцией и, следовательно, 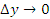 при ∆ x → 0. Тогда
при ∆ x → 0. Тогда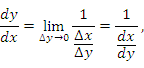
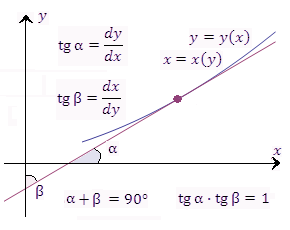
 ,
,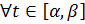
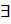 производные функции x(t), y(t),
производные функции x(t), y(t),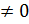
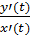
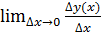 =
= 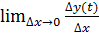
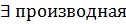 x’(t), то функция x=x(t) непрерывна, значит, по второму определению непрерывности:
x’(t), то функция x=x(t) непрерывна, значит, по второму определению непрерывности: 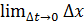 =0, т.е.
=0, т.е.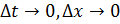
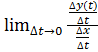 =(по свойству пределов)
=(по свойству пределов) 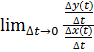 = =
= = 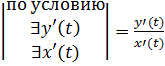 , Ч.Т.Д.
, Ч.Т.Д.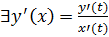 – функция
– функция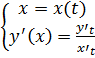
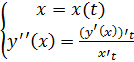
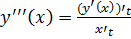 , тогда
, тогда 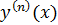 =
= 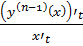
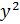 )’=1*
)’=1* 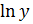 )’=
)’=  *y’(x)
*y’(x)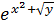 )’=
)’= 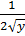 *y’(x))
*y’(x))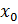 ), надо подставить координаты точки в выражение производной
), надо подставить координаты точки в выражение производной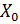 , то она в этой точке непрерывна
, то она в этой точке непрерывна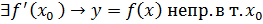 По условию теоремы
По условию теоремы 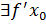 тогда по определению производной
тогда по определению производной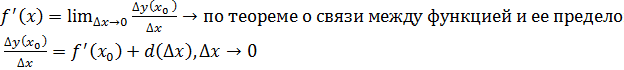
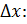
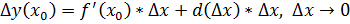
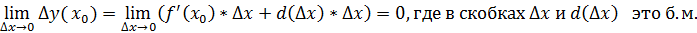
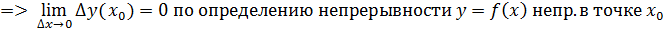
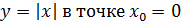
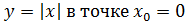
 , тогда
, тогда 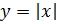 получит приращение
получит приращение 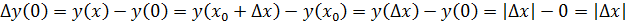
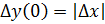
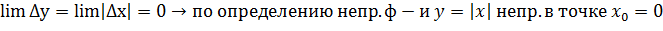
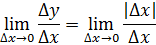
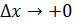
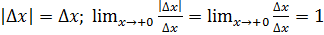
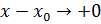
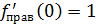
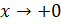
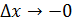
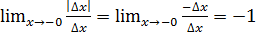
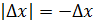
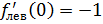
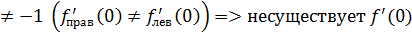
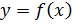 непр. в т.
непр. в т. 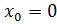 не имеет производной в т.
не имеет производной в т. 
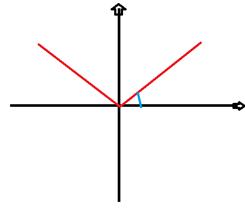 y=-x y y=x
y=-x y y=x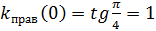

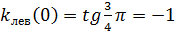
 непрерывна на отрезке
непрерывна на отрезке 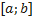 , дифференцируема на
, дифференцируема на  , то найдется хотя бы одна точка
, то найдется хотя бы одна точка  такая, что
такая, что 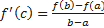 .
.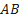 , стягивающей эту дугу.
, стягивающей эту дугу.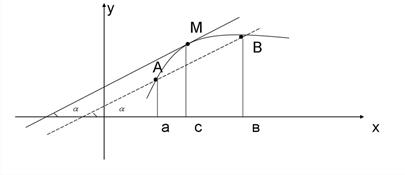
 – непрерывна на
– непрерывна на 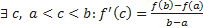
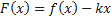 , где
, где 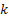 – угловой коэффициент
– угловой коэффициент  ,
,  ,
, 
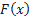 – удовлетворяет условиям теоремы Ролля:
– удовлетворяет условиям теоремы Ролля: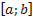 ;
;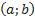 ;
;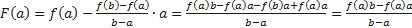

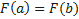
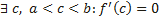 ,
,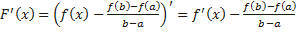
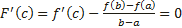
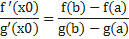
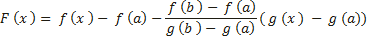

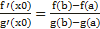
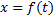 ,
, 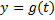 , где параметр
, где параметр  изменяется в промежутке
изменяется в промежутке  . При изменении параметра
. При изменении параметра  до
до  . В соответствии с теоремой Коши на кривой
. В соответствии с теоремой Коши на кривой  найдется точка
найдется точка 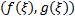 , в которой касательная параллельна хорде, соединяющей концы
, в которой касательная параллельна хорде, соединяющей концы  и
и  данной кривой.
данной кривой.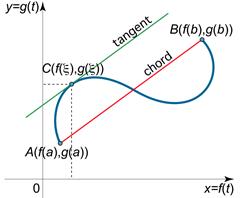
 в точке
в точке  . Определение дифференциала
. Определение дифференциала 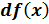 . Геометрический смысл дифференциала
. Геометрический смысл дифференциала 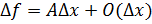 , где
, где 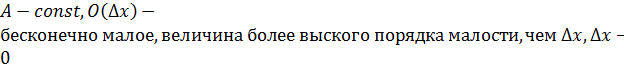
 называется дифференцированной в точке, если приращение в этой точке допускает выделение главной части линейной приращения аргумента
называется дифференцированной в точке, если приращение в этой точке допускает выделение главной части линейной приращения аргумента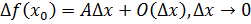
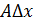 – главная по значению линейная относительно
– главная по значению линейная относительно 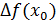 , называется главная часть
, называется главная часть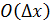 – бесконечно малое более высокого порядка малости, чем
– бесконечно малое более высокого порядка малости, чем 
 равен приращения независимой переменной
равен приращения независимой переменной 
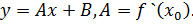
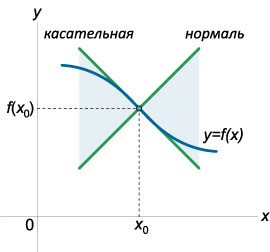
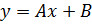 имеет угловой коэффициент
имеет угловой коэффициент  и проходит через точку
и проходит через точку 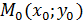 ,
, 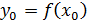 , данная прямая – касательная к графику функции в точке
, данная прямая – касательная к графику функции в точке 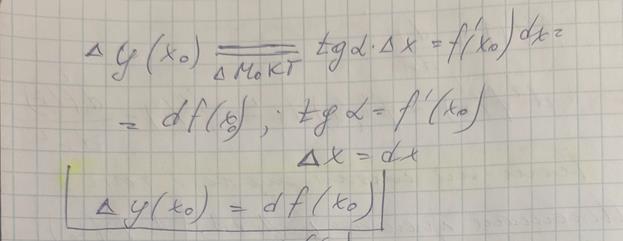
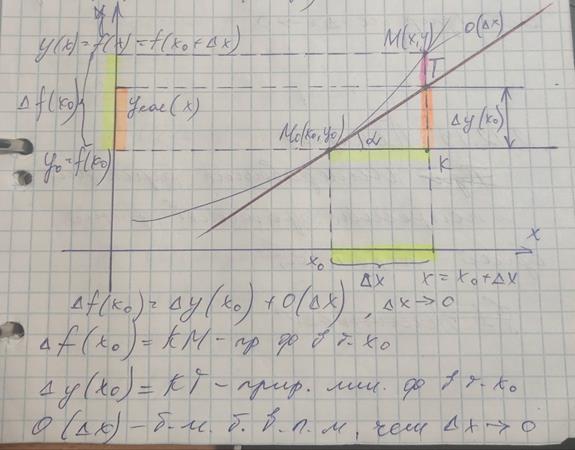 Дифференциал функции в точке
Дифференциал функции в точке 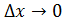
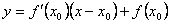 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.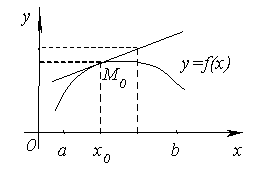
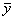 ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда 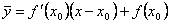 . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 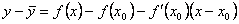 .
.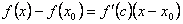 , где c между x и x 0.
, где c между x и x 0.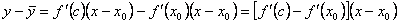 .
.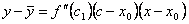 , где c 1 между c 0 и x 0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
, где c 1 между c 0 и x 0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. (x – x 0) > 0 и (c – x 0) > 0. Поэтому
(x – x 0) > 0 и (c – x 0) > 0. Поэтому 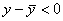 .
.
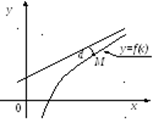
 .
. 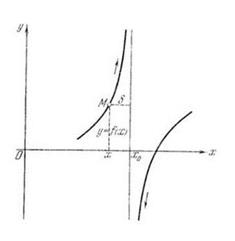
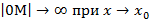
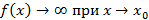 ,или хотя бы один из односторонних пределов бесконечен
,или хотя бы один из односторонних пределов бесконечен 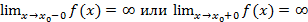 , то
, то 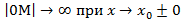 , следовательно по определению ВА
, следовательно по определению ВА 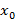
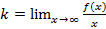 ,
, 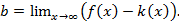
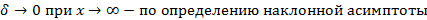
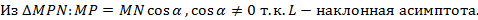
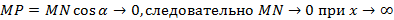
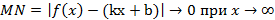
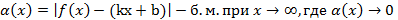
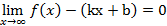
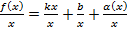 ,
, 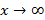
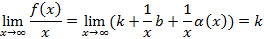
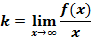
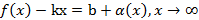
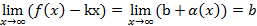
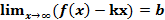
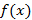 .
. 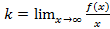 ,
, 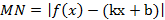
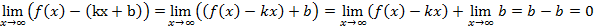
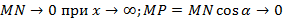 (по определению НА): L: y=kx+b – НА графика функции
(по определению НА): L: y=kx+b – НА графика функции 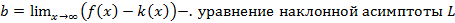
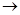 x
x  . Геометрическая интерпретация. Доказательство теоремы о разности функции и ее предела.
. Геометрическая интерпретация. Доказательство теоремы о разности функции и ее предела.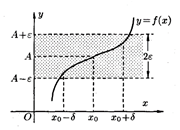
 x
x  Геометрическая интерпретация. Доказательство теоремы о связи бесконечно большой и бесконечно малой.
Геометрическая интерпретация. Доказательство теоремы о связи бесконечно большой и бесконечно малой.