Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложная функция, непрерывность сложной функции.
Пусть функция u=u(x) определена для ∀х ∈ D (D-область определения функции u=u(x)), пусть область значения функции u=u(x) - множество G, т.е. u ∈ G. Рассмотрим в области G функцию y=f(u), причем множество значений u содержится в области определения функции f(u), тогда каждому x по правилу f(u(x)) можно сопоставить число y=(f(u(x))).
Внутренняя функция Независимая переменная Пусть функции u=u(x) непрерывна в точке x₀, а функция y=f(u) непрерывна в точке u₀=u(x₀). Тогда сложная функция f(u(x)), состоящая из непрерывных функций, непрерывна в точке x₀.
Это и доказывает, что сложная функция y=f(u(x)) непрерывна в точке x₀. 11. Определение производной функции y=f(x), ее геометрический смысл (обоснование). Уравнение касательной и нормали к кривой y=f(x) ❶ Определение
Обозначения:y’(x); f’(x);
❷ Геометрический смысл производной Y Г M
Δ Y α β M 0 К X
x 0 Δ x x = x 0 + Δ x
Пусть кривая Г задается уравнением y=f(x). Возьмем произвольную точку на прямой Г (точка М0). М0М – секущая графика функции y=f(x). М ∈ Г. Устремим точку М к точке М0 по графику функции; получим новую секущую. Секущая М0М, меняя положение, займет в пределе положение касательной.
Подставив (2) в (1) получим: ●
Тогда:
Геометрический смысл производной: “Значение производной функции f(x) в точке x0 равно угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой x0 .” ❸ Уравнение касательной к кривой y=f(x)
Уравнение касательной к графику функции f(x)– это уравнение прямой, проходящей через точку М0 (x0,y0). По геометрическому смыслу производной в точке
❹ Уравнение нормали к кривой y=f(x)
Нормалью к графику функции f(x) в точке М0 называется перпендикуляр, проведенный к касательной в точке касания М0 (x0, y0).
Уравнение нормали к графику функции y = f(x) в точке М0 - это уравнение прямой по точке М0 (x0,y0) и угловому коэффициенту нормали, который равен
12.Вывод формулы для производных функций y=e x, y=ln x, y= sin x, y=tg x, y=a x, y=loga x. y=sinx
Воспользуемся формулой разности синусов:
y=tgx . y=a^x
Пришли к неопределенности. Для ее раскрытия введем новую переменную
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.228.88 (0.006 с.) |

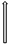
 Внешняя функция
Внешняя функция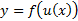
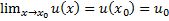 , т.е.при x→x₀ имеем u→u₀. Поэтому, вследствие непрерывности функции y=f(u) имеем:
, т.е.при x→x₀ имеем u→u₀. Поэтому, вследствие непрерывности функции y=f(u) имеем: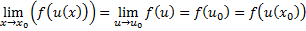
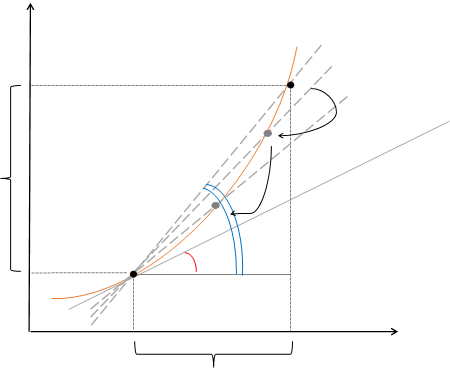 Производной функции y = f (x) в точке x называется предел отношения приращения функции в этой точке, к приращению аргумента, когда приращение аргумента стремится к нулю.
Производной функции y = f (x) в точке x называется предел отношения приращения функции в этой точке, к приращению аргумента, когда приращение аргумента стремится к нулю.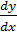 ;
; 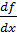
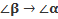 ;
; 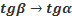 ;
; 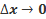 ⇒
⇒ 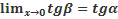 (1)
(1)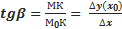 (2)
(2)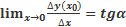
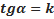 - угловой коэффициент касательной графика функции y = f (x)
- угловой коэффициент касательной графика функции y = f (x)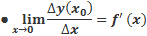
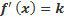
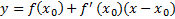
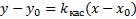
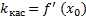 Тогда
Тогда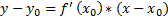
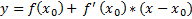 – искомое уравнение касательной.
– искомое уравнение касательной.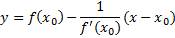
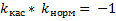 ⇒
⇒ 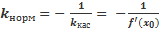
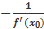 .
.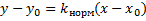
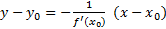
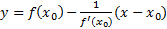 - искомое уравнение нормали
- искомое уравнение нормали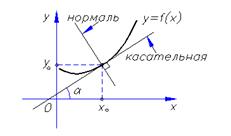
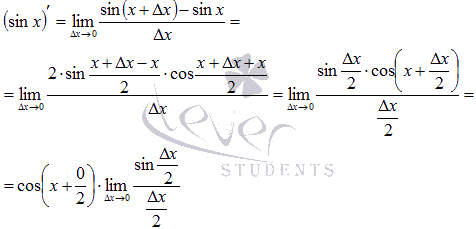
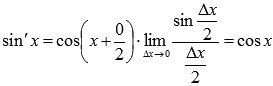
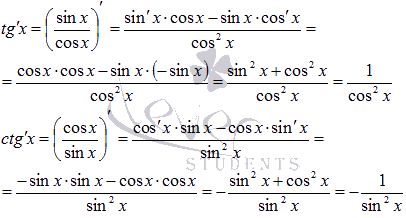
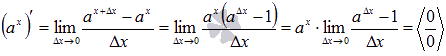
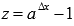 , причем
, причем 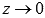 при
при 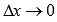 . Тогда
. Тогда 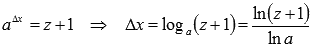 . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
. В последнем переходе мы использовали формулу перехода к новому основанию логарифма.