
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Основы дифференциального исчисления
3.1 Общие правила дифференцирования. Производные элементарных функций. Техника дифференцирования
Правила дифференцирования:
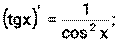
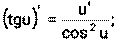
1) 2) 3) 4) Ниже приведена таблица производных. Левая колонка таблицы пояснений не требует, правая же представляет собой производные сложных функций. Смысл формул, стоящих справа, можно выразить таким образом: производная сложной функции равна произведению производной внешней функции по своему аргументу на производную внутренней функции по своему аргументу.
Здесь u=u(x) и v=v(x) – дифференцируемые функции.
Пример 15. Найдите производные функций: 1) 2) 3) 4) Решение: 1) Сначала преобразуем функцию, используя определения степени с рациональным показателем.
Теперь для вычисления производной используем формулы (1), (3), (7)
2) Воспользуемся формулами (1), (5), (6), (14)
3) Функция f(x) представляет из себя произведение двух функций u(x)= v(x)=
далее необходимо применить формулы (1), (3),(8), (13), (16)
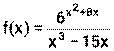
4) Функция f(x) представляет из себя частное двух функций u(x)= v(x)=
Далее необходимо применить формулы (1), (5), (6), (9)
Литература: [1] стр. 154-168, [2] стр. 148-151, 155-167,170-176, 178 [3] стр. 205-207, 210-213, 215, [4] стр. 204-231, [5] стр. 87-91 3.2Производные высших порядков. Физический смысл производной
Пусть материальная точка движется прямолинейно по закону S=S(t), тогда 1) Скорость прямолинейного движения материальной точки в момент времени t равно первой производной от пути по времени.
2) Ускорение прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или второй производной от пути по времени
Пример 16. Тело движется прямолинейно по закону
Решение: 1)
2)
Ответ: в момент времени t=1 скорость тела равна 5 м/с, а ускорение равно 3 м/с2.
Литература: [1] стр. 173-175, [2] стр. 179-180, [3] стр. 209, 218 -219, [4] стр. 237-242, [5] стр. 120-121
3.3 Геометрический смысл производной. Уравнение касательной и нормали к плоской кривой
Производная функции в точке равна угловому коэффициенту касательной, проведённой к графику функции в этой точке. Уравнение касательной к графику функции у = f(х) в точке с абсциссой х0 имеет вид:
Уравнение нормали к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
Алгоритм составления уравнения касательной и нормали 1. Обозначьте абсциссу точки касания х0. 2. Вычислите f(х0). 3. Найдите 4. Найденные значения х0, f(х0), 5. Выполните упрощение, полученных уравнений.
Пример 17. Составьте уравнение касательной к графику функции f(х)=х2+6х+5 в точке с абсциссой х0 = -2. Решение. 13) х0=-2 14) f(х0)=(-2)2+6(-2)+5= -3 15) 16) касательная: у= -3+2(х-(-2)) у= -3+2(х+2) у= -3+2х+2 у=2х+1 5. нормаль: Ответ: у=2х+1 – уравнение касательной,
Литература: [1] стр. 139-144, [2] стр. 199-201, [3] стр. 207-209, [4] стр. 231-236, [5] стр. 87-91
3.4 Исследование функции с помощью производной. Построение графика функции. Справочный материал
Достаточные условия монотонности (возрастания, убывания) функции: 1. Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке возрастает. 2. Если производная дифференцированной функции отрицательна на промежутке, то функция на этом промежутке убывает.
Необходимое и достаточные условия экстремума функции: 1. Если функция имеет экстремум в точке, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует 2. Если в стационарной точке х=а производная функции меняет свой знак с плюса на минус (с возрастания на убывание), то функция в этой точке имеет максимум, если с минуса на плюс, то функция имеет минимум.
Алгоритм определения промежутков монотонности и экстремумов функции 1. Найдите область определения функции.
2. Найдите производную функции. 3. Найдите стационарные и критические точки, т. е точки в которых производная функции равна нулю или не существует. 4. Отметьте стационарные и критические точки на числовой прямой и определите знаки производной на получившихся промежутках. 5. Сделайте выводы (стрелками) о монотонности функции. 6. Сделайте выводы о точках экстремума функции.
Достаточные условия выпуклости и вогнутости графика функции: 1. Если для дважды дифференцируемой функции вторая её производная отрицательна внутри промежутка, то график функции является выпуклым на данном промежутке. 2. Если же вторая производная положительна внутри промежутка, то график функции является вогнутым на данном промежутке.
Алгоритм определения промежутков выпуклости и вогнутости графика функции 1. Найдите вторую производную функции. 2. Найдите стационарные и критические точки второго рода, т. е. точки в которых вторая производная равна нулю или не существует. 3. Отметьте стационарные и критические точки второго рода на числовой прямой и определите знаки второй производной на получившихся промежутках. 4. Сделайте выводы о промежутках выпуклости, вогнутости и точках перегиба графика функции.
Схема исследования функции 1. Найдите область определения функции. 2. Определите четность, нечетность функции. 3. Найдите производную функции. 4. Определите стационарные и критические точки производной. 5. Определите промежутки монотонности и экстремумы функции. 6. Найдите значения функции в стационарных и критических точках. 7. Найдите вторую производную и исследуйте функцию на выпуклость и вогнутость. 8. Для построения графика найдите необходимые дополнительные точки.
Пример 18. Исследуйте функцию и постройте график f(x)=3х2-х3 1) 2) f(-x)=3(-х)2-(-х)3=3х2+х3 – функция общего вида, т.к. f(-x)≠ f(x) f(-x)≠ f(-x) 3) 4) х=0; х=2 – стационарные точки, критических точек нет 5)
6) х=0 точка минимума, х=2 точка максимума f(0)=0; f (2)==4 7) =0, 6-6х=0 6(1-х)=0 х=1
‹ 0 › 0 х=1 – точка перегиба f(1)==2
8) Дополнительные точки f(-1)= f(3)=
9) Построим график функции. Для этого сначала на координатной плоскости отметим точки максимума и минимума, дополнительные точки, точки перегиба, а затем построим график.
Литература: [1] стр. 183-187, 191-192,196-198, [2] стр. 182-187, [3] стр. 220-236, [4] стр. 255-268, [5] стр. 87-91 3.5 Асимптоты графика функции Вертикальные асимптоты:
Вертикальные асимптоты следует искать в точках разрыва второго рода функции или на границе области допустимых значений аргумента. Если или или, то х=а - вертикальная асимптота.
Горизонтальные асимптоты:
Если, то y=b - горизонтальная асимптота (b – конечное число).
Наклонные асимптоты:
Прямая y=kx+b является наклонной асимптотой, если
Схема исследования функции
Пример 19. Исследуйте функцию и постройте график f(x)= 1) т.к. при х=0 знаменатель обращается в ноль. 2) Точка разрыва х=0 – точка разрыва второго рода, т. к. , х=0 – вертикальная асимптота 3) f(-x)= – функция общего вида, т.к. f(-x)≠ f(x) f(-x)≠ f(-x) 4) = 5) =0, х3-8=0 х=2 – стационарная точка, не существует при х=0, х=0 - критическая точка.
6) 7)
8) х=2 точка минимума f(0)=; f (2)= 9) =0 не может быть, - не существует при х=0
> 0 › 0
10) Наклонные асимптоты:
у=х – наклонная асимптота 11) Горизонтальные асимптоты:
горизонтальных асимптот нет 12) Дополнительные точки f(-1)= f(1)= f(3)= 12) Построим график функции. Для этого сначала на координатной плоскости отметим точку минимума, дополнительные точки, проведём асимптоты, а затем построим график.
Литература: [1] стр. 194-198, [3] стр. 231-236, [5] стр. 146-151 3.6 Наибольшее и наименьшее значение функции на отрезке Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке 1. Найти производную функции. 2. Определить стационарные точки функции. 3. Вычислить значения функции на концах отрезка и в стационарных точках, принадлежащих этому отрезку. 4. Выбрать наибольшее и наименьшее значения и записать ответ. Пример 20 Найдите наименьшее и наибольшие значения функции у=х3-3х2-45х+1 на отрезке. Решение Воспользуемся алгоритмом: 1. Имеем. 2. Производная существует при всех х, значит, стационарные точки находим из условия
у(0)=1 у(6)= -161 у(5)= -174
Ответ: на отрезке унаиб=у(0)=1, yнаим=у(5)= -174. Литература: [1] стр. 187-188, [2] стр. 195-205, 209-211, [3] стр. 236-267, [4] стр. 268-270, 274 -286, [5] стр. 140-146
Глава 4. Основы интегрального исчисления 4.1 Первообразная функции. Неопределённый интеграл. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F’(x) = f(x).
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Таблица интегралов: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) Пример 21.
Решение: Сначала выполним преобразования, а затем воспользуемся формулой (1)
Литература: [1] стр. 213-216, [2] стр. 229-235, 239-240, [3] стр. 247-255, [4] стр. 290-306, 274 -286, [5] стр. 159-163 4.2 Интегрирование подстановкой в неопределённом интеграле
формула замены переменной в неопределённом интеграле
План интегрирования способом подстановки.
1. Определяют к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно). 2. Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену. 3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной. 4. Производят замену под интегралом. 5. Находят полученный интеграл. 6. В результате производят обратную замену, т. е. переходят к старой переменной. Результат можно проверить дифференцированием.
Пример 22.
Решение:
Правило 1: Если подынтегральная функция имеет вид f(ax+b), то может оказаться полезной подстановка t=ax+b. Пример 23.
Иногда перед тем как сделать подстановку подынтегральное выражение надо преобразовать.
Пример 24.
Пример 25
Правило 2: Пусть подынтегральное выражение разбито на два сомножителя и в одном из них легко распознать дифференциал функции ϕ(х). Может оказаться, что после подстановки t=ϕ(х) второй сомножитель превратиться в такую функцию от t, которую легко проинтегрировать. Тогда подстановка окажется полезной.
Пример 26.
Пример 27.
Пример 28.
Литература: [1] стр. 217-218, [2] стр. 240-242, [3] стр. 255-261, [4] стр. 310-316, 274 -286, [5] стр. 163-165 4.3 Понятие определённого интеграла. Интегрирование подстановкой в определённом интеграле Определение: Если F(x)+C первообразная функции f(x), то приращение F(b)-F(a) первообразной функции при изменении аргумента х от х=а до х=b называется определённым интегралом и обозначается символом, т,е
формула Ньютона-Лейбница Теорема: Пусть функция f(t) непрерывна в любой точке t=ϕ(x), где x∈[á,â] и пусть a=ϕ(á), b=ϕ(â). Тогда если функция ϕ(х) имеет непрерывную производную, то справедлива следующая формула.
формула замены переменной в определённом интеграле
Для вычисления определённого интеграла способом подстановки поступают так же, как и при вычислении неопределённого интеграла этим способом. Однако нужно помнить одну особенность: в случае определённого интеграла нет необходимости возвращаться к первоначальной переменной, но нужно помнить, что заменяя переменную под знаком интеграла следует изменить и пределы интегрирования.
План интегрирования способом подстановки. 1. Определяют к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно). 2. Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену. 3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной. 4. Находят новые пределы интегрирования. 5. Производят замену под интегралом. 6. Находят полученный интеграл.
Правило 1: Если подынтегральная функция имеет вид f(ax+b), то может оказаться полезной подстановка t=ax+b.
Пример 29.
Иногда перед тем как сделать подстановку подынтегральное выражение надо преобразовать. Пример 30
Правило 2: Пусть подынтегральное выражение разбито на два сомножителя и в одном из них легко распознать дифференциал функции ϕ(х). Может оказаться, что после подстановки t=ϕ(х) второй сомножитель превратиться в такую функцию от t, которую легко проинтегрировать. Тогда подстановка окажется полезной. Пример 31.
Литература: [1] стр. 228-236, [2] стр. 253-255, 260-263, 266-268, [3] стр. 267-281, [4] стр. 322, 325-331, 274 -286, [5] стр. 192-195
4.4 Физические приложения определённого интеграла 4.4.1 Нахождение пути, пройденного телом при прямолинейном движении. Как известно, путь, пройденный телом при равномерном движении за время t, вычисляется по формуле S=v t. Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени, т.е. v=f(t),то для нахождения пути, пройденного телом за время от t=a до t=b, можно воспользоваться формулой
Пример 32 Найти путь, пройденный телом за три секунды и за третью секунду движения, если его скорость задается формулой v(t)=e2х м/с.
Решение: 1). Путь, пройденный за три секунды: 2).Путь, пройденный за третью секунду: Ответ: 1) за три секунды тело пройдёт путь 201,121(м); 2) за третью секунду тело пройдёт путь 198,02 (м) 4.4.2 Нахождение работы переменной силы. Пусть под действием переменной силы F(x) тело перемещается из точки х=а в точку х=b. Тогда работа силы F(x) по перемещению тела находится по формуле:
Силой в 40 Н пружина растягивается на 8 см. Первоначальная длина пружины равна 10 см. Какую работу надо совершить, чтобы растянуть пружину до 15 см? Решение: При растяжении пружины сила воздействия F(x) численно равнa силе упругости Fупр=kx, где k- жесткость пружины, х- абсолютное удлинение. Найдем жесткость пружины: k=F(x)/x= 40H/0,08м= 500 Н/м Тогда F(x) = 500x, пружину необходимо растянуть на 15-10=5см=0,05м и тогда работа равна Ответ:для растяжении пружины до 15 см необходимо совершить работу 0,625 (Н).
4.4.3Вычисление силы давления жидкости на вертикально расположенную пластину.
По закону Паскаля сила давления жидкости на вертикально расположенную пластину равна силе давления жидкости на горизонтально расположенную пластину той же площади погруженную на ту же глубину. Сила давления жидкости на вертикально расположенную пластину вычисляется по формуле:
Где у=f(x) – функция, выражающая зависимость длины поперечного сечения пластины от уровня погружения х, g- ускорение свободного падения, - плотность жидкости.
Пример 34 Определить силу давления воды на вертикальную пластинку длиной 20м и высотой 8м, верхнее основание которой находиться ниже поверхности жидкости на 2м. Решение:
f(x) =20, a=2, b=8+2=10, g=1000кг/м3, тогда сила давления жидкости Р=9,81·1000 · Ответ: Сила давления жидкости на пластинку равна 9,418∙106(Н).
Пример 35 Вычислить силу давления воды на треугольную пластину АВС с основанием АС=9м и высотой ВD=2м, вертикально погруженную в жидкость, если вершина В лежит на свободной поверхности жидкости, а АС параллельна ей. Решение: Пусть MN –поперечное сечение пластины на уровне ВЕ =х. Найдем зависимость длины MN от х.Из подобия треугольников MNB и АВС имеем: или. Отсюда MN=f(x)=4,5·x. Тогда f(x) =4,5х, a=0, b=BD=2, g=1000кг/м3 В
M E N
A C D
Ответ: Сила давления жидкости на пластинку равна 1,177∙105(Н).
Литература: [1] стр. 228-235, [2] стр. 302-305, [3] стр. 293-294, [4] стр. 355-363
4.5 Геометрические приложения определённого интеграла
4.5.1 Вычисление площади плоской фигуры Если интегрируемая на отрезке [a;b] функция f(x) неотрицательна, то определённый интеграл равен площади криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а, х= b.
Если фигура ограничена двумя кривыми y=f(x), y=g(x) и прямыми х=а, х= b, где a≤x≤b и f(x)≤g(x), то её площадь вычисляется по формуле:
Пример 36 Найти площадь фигуры, ограниченной параболой и прямой Решение: Построим графики функций:
Видно, что они пересекаются в двух точках, абсциссы которых х=-3 и х=6. На отрезке [-3;6] выше проходит график функции, поэтому
Ответ: площадь фигуры 13,5 (ед2). 4.5.2 Нахождение длины дуги кривой Пусть кривая АВ задана уравнением y=f(x) и переменная х определена на отрезке [а,b], причём f(x) – непрерывная функция на этом промежутке. Тогда длина дуги вычисляется по формуле:
Пример 37
Найти длину дуги параболы у=-х2+8х-12, если 2≤х≤5. Решение: Построим график функции.
Сделаем подстановку
Вычислим интеграл, используя формулу:
Ответ: длина дуги параболы 6,126 (ед). 4.5.3 Вычисление объёма тела вращения Поверхность, полученная путём вращения кривой y=f(x) вокруг оси ОХ, называется поверхностью вращения. Прямая ОХ называется осью поверхности вращения, а объём, рассматриваемого тела вращения, вычисляется по формуле:
Пример 38 Найти объём тела, полученного вращением вокруг оси ОХ криволинейной трапеции, соответствующей функции у=х3, х[1;3]. Решение: Построим график функции у=х3 и выполним объёмный чертёж
Вычислим объём тела вращения:
Ответ: объём тела вращения равен 981,075 (ед3).
4.5.4 Вычисление площади поверхности вращения Площадь поверхности образованной вращением кривой y=f(x) вокруг оси ОХ, вычисляется по формуле:
Пример 39
Найти площадь поверхности тела, полученного вращением вокруг оси ОХ криволинейной трапеции, соответствующей функции у=3х-5, х[2;3]. Решение: Построим график функции у=3х-5 и выполним объёмный чертёж
Ответ: площадь поверхности вращения равна 49,673 (ед2).
Литература: [1] стр. 245-252, [2] стр. 290-301, [3] стр. 278-281, 283-288, 291-293, [4] стр. 331-343, [5] стр. 197-207
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.150.59 (0.307 с.) |
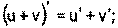
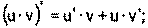
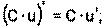
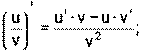
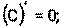
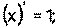
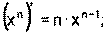
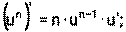
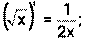
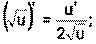
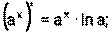
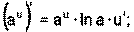
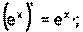
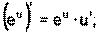
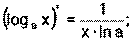
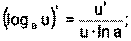
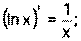

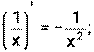
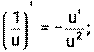
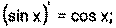
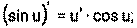
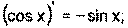

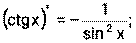
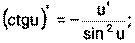
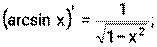
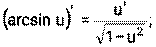
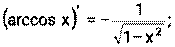
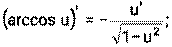
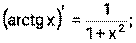
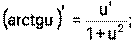
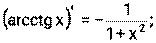
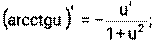
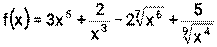 ;
;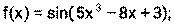
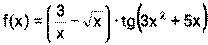 ;
; .
.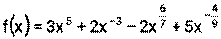 .
.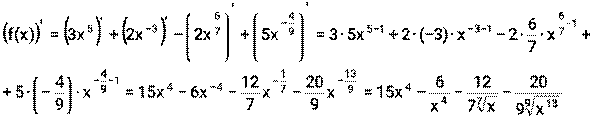
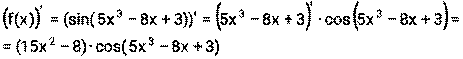
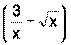 и
и , поэтому надо воспользоваться формулой (2)
, поэтому надо воспользоваться формулой (2)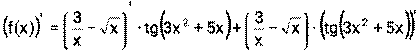
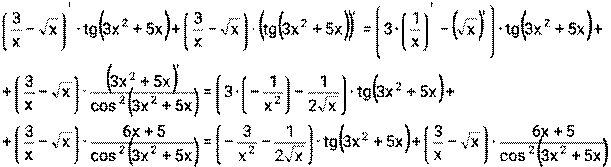
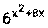 и
и , поэтому надо воспользоваться формулой (4)
, поэтому надо воспользоваться формулой (4)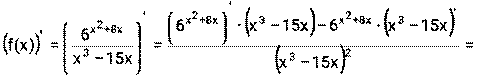
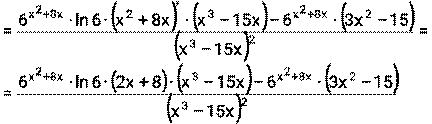
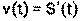
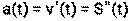
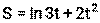 , где S – путь (м ), t- время (с). Найти скорость и ускорение тела в момент времени t=1с.
, где S – путь (м ), t- время (с). Найти скорость и ускорение тела в момент времени t=1с.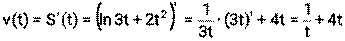
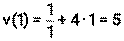 (м/с)
(м/с)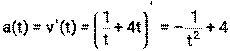
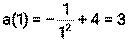 (м/с2)
(м/с2)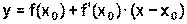
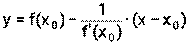
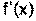 и вычислите
и вычислите 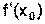 .
.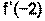 =2(-2)+6=2
=2(-2)+6=2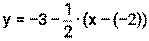
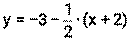
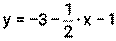
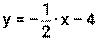
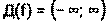 .
.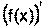 =(3х2-х3)=6х-3х2=3х(2-х)
=(3х2-х3)=6х-3х2=3х(2-х)


