
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Вычисление геометрических величинСтр 1 из 6Следующая ⇒
МАТЕМАТИКА
Методические указания и контрольные задания для студентов-заочников
Составители: Масыгина И. А., Корчуганова И.Б. преподаватели колледжа
Череповец
2016 Математика. Методические указания и контрольные задания для студентов-заочников. /Составители: Масыгина И. А., Корчуганова И.Б./ Череповец: Череповецкий металлургический колледж, 2016, 77с.
Рецензенты
Данные методические рекомендации рассмотрены и одобрены цикловой комиссией математических и естественно-научныных дисциплин
Председатель /Масыгина И. А./ СОДЕРЖАНИЕ
Рекомендации по выполнению и оформлению контрольной работы
Цель преподавания математики в колледже – познакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач, привить студентам умение самостоятельно изучать учебную литературу по математике, развить логическое мышление и повысить общий уровень математической культуры.
Настоящее пособие для студентов-заочников содержит методические указания и контрольные задания по темам, изучаемым в рамках дисциплины «Математика».
Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по учебным пособиям, рекомендуемым в данной книге. В настоящем пособии указаны учебники, имеющиеся в библиотеке колледжа, или недавно вышедшие и поэтому имеющиеся в книжных магазинах, естественно студент вправе использовать и другую литературу: учебники для техникумов, колледжей, ВУЗов, лекции, справочники, возможно также использование Интернет-ресурсов – главное правильность выполнения заданий. В настоящем пособии даются некоторые начальные теоретические сведения и приводятся решения типовых примеров.
Каждый студент выполняет тот вариант контрольной работы, который соответствует его порядковому номеру в алфавитном списке. Решение задач необходимо приводить в той же последовательности, что и в условиях задач. Перед этим условие задачи должно быть полностью переписано перед её решением.
В прорецензированной контрольной работе студент должен исправить отмеченные рецензентом ошибки и учесть его рекомендации и советы.
ЖЕЛАЕМ УСПЕХА! Пример 3
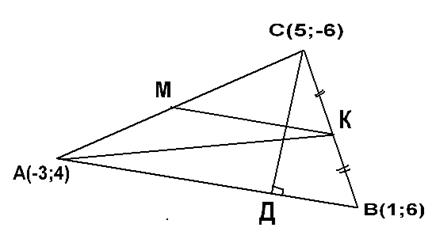
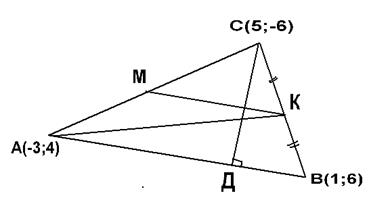
Дан треугольник АВС А(-3;4), В(1;6), С(5;-6). Найдите а) длину медианы АК, б) длину средней линии КМ║АВ, в) координаты точки N пересечения медиан, г) периметр, д) площадь, е)высоту СД.
Решение: 1) Выполним рисунок. На рисунке отметим координаты данных точек.
1) Длина медианы АК: По определению медианы: К – середина стороны ВС Длина отрезка АК: 2) Длина средней линии КМ║АВ По свойству средней линии, её длина равна половине той стороны, которой она параллельна. Найдём длину стороны АВ
Найдём длину КМ
3) Координата точки N пересечения медиан Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины. Значит точка N делит медиану АК в отношении 2:1, т.е.
4) Периметр – это сумма длин всех сторон треугольника.
6) Площадь можно найти по формуле Герона S=
5) Высота СД опущена на сторону АВ.
Литература: [1] стр. 4-9, [2] стр. 71-73, [3] стр. 4-5, 8-13, [4] стр. 125-406 [5] стр. 34-43
1.4 Линейные действия над векторами в координатной форме Если началом вектора является точка А(ха;уа;za), а концом точка В(хb;уb;zb), то координаты этого вектора вычисляются по формуле;
Длина вектора Координаты суммы двух и более векторов равны суммам соответствующих координат слагаемых, т. е. если Координаты разности двух и более векторов равны разностям соответствующих координат этих векторов, т. е. если Координаты произведения вектора на число равны произведениям соответствующих координат данного вектора на это число, т. е. если
Пример 4
Даны точки А(5,6,-9), В(-7,4,-2), С(-6,11,0). Найти координаты векторов Решение:
Литература: [1] стр. 50-51, [2] стр. 67-68, [3] стр. 478-482, [4] стр. 141-152 [5] стр. 222-231
1.5 Линейные действия над векторами в геометрической форме
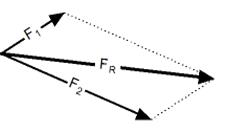
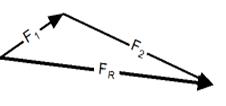
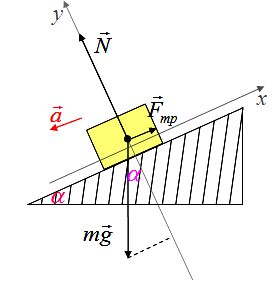
Правило параллелограмма. Процедура сложения векторов по правилу параллелограмма заключается в следующем: ● нарисовать первый вектор, учитывая его величину и направление ● от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление ● дополнить рисунок до параллелограмма, считая, что два нарисованных вектора - это его стороны ● результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора Правило треугольника Сложение векторов по правилу треугольника заключается в следующем: ● нарисовать первый вектор, используя данные о его длине (числовой величине) и направлении ● от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление ● результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец - с концом второго . Эти правила используются в механике для нахождения равнодействующей силы. Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
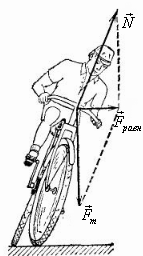
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Любой вектор
Пример 5. Найти длины проекций вектора Решение:
1.6 Уравнение прямой на плоскости Уравнение прямой на плоскости Ах+Ву+С=0
Направляющий вектор Нормальный вектор
Чтобы написать уравнение прямой надо: 1) Найти координаты направляющего или нормального вектора прямой. 2) Используя их, определить А и В (
3) Найти С=-(А∙х+В∙у), где х, и у –координаты точки через которую проходит прямая.
Пример 6 Дан треугольник АВС А(-3;4), В(1;6), С(5;-6). Найдите а) уравнение стороны ВС, б) уравнение медианы АК, в) уравнение средней линии КМ║АВ,, д) уравнение высоты СД. Решение: 1) Выполним рисунок. На рисунке отметим координаты данных точек.
2) Уравнение стороны ВС: направляющим вектором стороны ВС является вектор Уравнение стороны ВС: -12х - 4у+36=0 3) Уравнение медианы АК: направляющим вектором медианы АК является вектор
точку А, Значит С= - (- 4∙(-3)+(-6)∙4)= - (-12)=12. Уравнение медианы АК: - 4х - 6у+12=0, или – 2х - 3у+6=0 4) Уравнение средней линии КМ║АВ: направляющим вектором средней линии КМ║АВ является вектор точку К, Значит С= - (2∙3+(-4)∙0)= - 6. Уравнение средней линии КМ║АВ: 2х - 4у – 6=0 5) Уравнение высоты СД: нормальным вектором высоты СД является вектор точку С, Значит С= - (4∙5+2∙(-6))= - 8. Уравнение высоты СД: 4х +2у -8=0.
Литература: [1] стр. 9-20, [2] стр. 122-132, [3] стр.333-334, [4] стр. 125-133 [5] стр. 43-69 Пример 8. Для комплексных чисел z1=5-8i, z2=3+4i вычислить а) z1+ z2, б) z1- z2, в) z1∙ z2 Решение: а) z1+ z2=(5-8i)+(3+4i)= 5-8i +3+4i=(5+3)+(-8i+4i)=8+(-8+4)∙i=8-4i; б) z1- z2=(5-8i)- (3+4i)= 5-8i- 3-4i=(5-3)+(-8i -4i)=2+(-8-4)∙i=2-12i; в) z1∙ z2=(5-8i)∙(3+4i)=15+20i-24i-32i2=15-4i+32=47-4i. Чтобы выполнить деление комплексных чисел производят дополнительное действие: умножают делимое и делитель на число сопряжённое делителю.
Пример 9. Для комплексных чисел z1=5-8i, z2=3+4i вычислить Решение:
Литература: [1] стр. 144-145, [2] стр. 83-93, [3] стр. 299-300, 283-288, 291-293, [4] стр. 107-111, [5] стр. 402-403
2.2 Три формы записи комплексных чисел
Для перехода от алгебраической формы записи комплексного числа к тригонометрической и показательной используют следующее правило: 1) Находят модуль комплексного числа по формуле 2) Определяют геометрически в какой четверти находится точка z. 3) Находят аргумент комплексного числа по формуле
4) Записывают комплексное число z в тригонометрической форме:
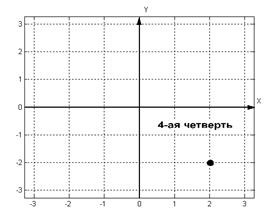
Пример 10. Комплексное число z=2-2i запишите в тригонометрической форме Решение: 1) z=2-2i, значит а=2, b=-2
2) Точка z(2;-2) находится в четвёртой четверти
3) Значит 4) Пример 11. Комплексное число z= - Решение: 1) z= -
2) Точка z(-
3) Значит 4) Для перевода комплексного числа из показательной формы в алгебраическую необходимо записать число в тригонометрической форме и выполнить вычисления. Пример 12.
Комплексное число Решение:
Литература: [1] стр. 145-146, 148,[2] стр. 96-103, 111-114, [3] стр. 300-302, [4] стр. 112-116, [5] стр. 404-405 2.3 Действия с комплексными числами в показательной и тригонометрической формах
Справедливы следующие равенства: 1) 2) 3) 4) 5) 6)
Пример 13. Для комплексных чисел z1= а) z1∙ z2, б) z1: z2, в) z13 Решение: а) б) в) Пример 14. Для комплексных чисел а) z1∙ z2, б) z1: z2, в) z14 Решение: а) б) в) Литература: [1] стр. 146-148, [2] стр. 103-107, 111-114, [3] стр. 302-303, [4] стр. 117-121
Пример 15. Найдите производные функций: 1) 2) 3) 4) Решение: 1) Сначала преобразуем функцию, используя определения степени с рациональным показателем.
Теперь для вычисления производной используем формулы (1), (3), (7)
2) Воспользуемся формулами (1), (5), (6), (14)
3) Функция f(x) представляет из себя произведение двух функций u(x)= v(x)=
далее необходимо применить формулы (1), (3),(8), (13), (16)
4) Функция f(x) представляет из себя частное двух функций u(x)= v(x)=
Далее необходимо применить формулы (1), (5), (6), (9)
Литература: [1] стр. 154-168, [2] стр. 148-151, 155-167,170-176, 178 [3] стр. 205-207, 210-213, 215, [4] стр. 204-231, [5] стр. 87-91 3.2Производные высших порядков. Физический смысл производной
Пусть материальная точка движется прямолинейно по закону S=S(t), тогда 1) Скорость прямолинейного движения материальной точки в момент времени t равно первой производной от пути по времени.
2) Ускорение прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или второй производной от пути по времени
Пример 16. Тело движется прямолинейно по закону
Решение: 1)
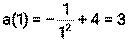
2)
Ответ: в момент времени t=1 скорость тела равна 5 м/с, а ускорение равно 3 м/с2.
Литература: [1] стр. 173-175, [2] стр. 179-180, [3] стр. 209, 218 -219, [4] стр. 237-242, [5] стр. 120-121
3.3 Геометрический смысл производной. Уравнение касательной и нормали к плоской кривой
Производная функции в точке равна угловому коэффициенту касательной, проведённой к графику функции в этой точке. Уравнение касательной к графику функции у = f(х) в точке с абсциссой х0 имеет вид:
Уравнение нормали к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
Пример 17. Составьте уравнение касательной к графику функции f(х)=х2+6х+5 в точке с абсциссой х0 = -2. Решение. 13) х0=-2 14) f(х0)=(-2)2+6(-2)+5= -3 15) 16) касательная: у= -3+2(х-(-2)) у= -3+2(х+2) у= -3+2х+2 у=2х+1 5. нормаль: Ответ: у=2х+1 – уравнение касательной,
Литература: [1] стр. 139-144, [2] стр. 199-201, [3] стр. 207-209, [4] стр. 231-236, [5] стр. 87-91
3.4 Исследование функции с помощью производной. Построение графика функции. Справочный материал
Достаточные условия монотонности (возрастания, убывания) функции: 1. Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке возрастает. 2. Если производная дифференцированной функции отрицательна на промежутке, то функция на этом промежутке убывает.
Необходимое и достаточные условия экстремума функции: 1. Если функция имеет экстремум в точке, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует 2. Если в стационарной точке х=а производная функции меняет свой знак с плюса на минус (с возрастания на убывание), то функция в этой точке имеет максимум, если с минуса на плюс, то функция имеет минимум.
Алгоритм определения промежутков монотонности и экстремумов функции 1. Найдите область определения функции. 2. Найдите производную функции. 3. Найдите стационарные и критические точки, т. е точки в которых производная функции равна нулю или не существует. 4. Отметьте стационарные и критические точки на числовой прямой и определите знаки производной на получившихся промежутках. 5. Сделайте выводы (стрелками) о монотонности функции. 6. Сделайте выводы о точках экстремума функции.
Достаточные условия выпуклости и вогнутости графика функции: 1. Если для дважды дифференцируемой функции вторая её производная отрицательна внутри промежутка, то график функции является выпуклым на данном промежутке. 2. Если же вторая производная положительна внутри промежутка, то график функции является вогнутым на данном промежутке.
Алгоритм определения промежутков выпуклости и вогнутости графика функции 1. Найдите вторую производную функции. 2. Найдите стационарные и критические точки второго рода, т. е. точки в которых вторая производная равна нулю или не существует. 3. Отметьте стационарные и критические точки второго рода на числовой прямой и определите знаки второй производной на получившихся промежутках. 4. Сделайте выводы о промежутках выпуклости, вогнутости и точках перегиба графика функции.
Схема исследования функции 1. Найдите область определения функции. 2. Определите четность, нечетность функции. 3. Найдите производную функции. 4. Определите стационарные и критические точки производной. 5. Определите промежутки монотонности и экстремумы функции. 6. Найдите значения функции в стационарных и критических точках. 7. Найдите вторую производную и исследуйте функцию на выпуклость и вогнутость. 8. Для построения графика найдите необходимые дополнительные точки.
Пример 18. Исследуйте функцию и постройте график f(x)=3х2-х3 1) 2) f(-x)=3(-х)2-(-х)3=3х2+х3 – функция общего вида, т.к. f(-x)≠ f(x) f(-x)≠ f(-x) 3) 4) х=0; х=2 – стационарные точки, критических точек нет 5)
6) х=0 точка минимума, х=2 точка максимума f(0)=0; f (2)==4 7) =0, 6-6х=0 6(1-х)=0 х=1
‹ 0 › 0 х=1 – точка перегиба f(1)==2
8) Дополнительные точки f(-1)= f(3)=
9) Построим график функции. Для этого сначала на координатной плоскости отметим точки максимума и минимума, дополнительные точки, точки перегиба, а затем построим график.
Литература: [1] стр. 183-187, 191-192,196-198, [2] стр. 182-187, [3] стр. 220-236, [4] стр. 255-268, [5] стр. 87-91 3.5 Асимптоты графика функции Вертикальные асимптоты:
Вертикальные асимптоты следует искать в точках разрыва второго рода функции или на границе области допустимых значений аргумента. Если или или, то х=а - вертикальная асимптота.
Горизонтальные асимптоты:
Если, то y=b - горизонтальная асимптота (b – конечное число).
Наклонные асимптоты:
Прямая y=kx+b является наклонной асимптотой, если
Схема исследования функции
Пример 19. Исследуйте функцию и постройте график f(x)= 1) т.к. при х=0 знаменатель обращается в ноль. 2) Точка разрыва х=0 – точка разрыва второго рода, т. к. , х=0 – вертикальная асимптота 3) f(-x)= – функция общего вида, т.к. f(-x)≠ f(x) f(-x)≠ f(-x) 4) = 5) =0, х3-8=0 х=2 – стационарная точка, не существует при х=0, х=0 - критическая точка.
6) 7)
8) х=2 точка минимума f(0)=; f (2)= 9) =0 не может быть, - не существует при х=0
> 0 › 0
10) Наклонные асимптоты:
у=х – наклонная асимптота 11) Горизонтальные асимптоты:
горизонтальных асимптот нет 12) Дополнительные точки f(-1)= f(1)= f(3)= 12) Построим график функции. Для этого сначала на координатной плоскости отметим точку минимума, дополнительные точки, проведём асимптоты, а затем построим график.
Литература: [1] стр. 194-198, [3] стр. 231-236, [5] стр. 146-151 3.6 Наибольшее и наименьшее значение функции на отрезке Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке 1. Найти производную функции. 2. Определить стационарные точки функции. 3. Вычислить значения функции на концах отрезка и в стационарных точках, принадлежащих этому отрезку. 4. Выбрать наибольшее и наименьшее значения и записать ответ. Пример 20 Найдите наименьшее и наибольшие значения функции у=х3-3х2-45х+1 на отрезке. Решение Воспользуемся алгоритмом: 1. Имеем. 2. Производная существует при всех х, значит, стационарные точки находим из условия
у(0)=1 у(6)= -161 у(5)= -174
Ответ: на отрезке унаиб=у(0)=1, yнаим=у(5)= -174. Литература: [1] стр. 187-188, [2] стр. 195-205, 209-211, [3] стр. 236-267, [4] стр. 268-270, 274 -286, [5] стр. 140-146
Глава 4. Основы интегрального исчисления 4.1 Первообразная функции. Неопределённый интеграл. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F’(x) = f(x). Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Таблица интегралов: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) Пример 21.
Решение: Сначала выполним преобразования, а затем воспользуемся формулой (1)
Литература: [1] стр. 213-216, [2] стр. 229-235, 239-240, [3] стр. 247-255, [4] стр. 290-306, 274 -286, [5] стр. 159-163 4.2 Интегрирование подстановкой в неопределённом интеграле
формула замены переменной в неопределённом интеграле
План интегрирования способом подстановки.
1. Определяют к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно). 2. Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену. 3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной. 4. Производят замену под интегралом. 5. Находят полученный интеграл. 6. В результате производят обратную замену, т. е. переходят к старой переменной. Результат можно проверить дифференцированием.
Пример 22.
Решение:
Правило 1: Если подынтегральная функция имеет вид f(ax+b), то может оказаться полезной подстановка t=ax+b. Пример 23.
Иногда перед тем как сделать подстановку подынтегральное выражение надо преобразовать.
Пример 24.
Пример 25
Правило 2: Пусть подынтегральное выражение разбито на два сомножителя и в одном
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.102.225 (0.435 с.) |
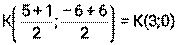
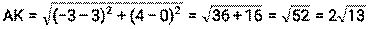
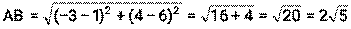
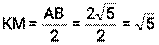
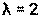
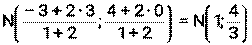
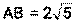
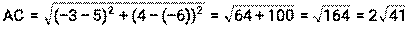
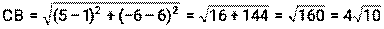
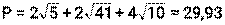
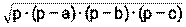 , где
, где 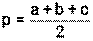 , a,b,c – длины сторон треугольника
, a,b,c – длины сторон треугольника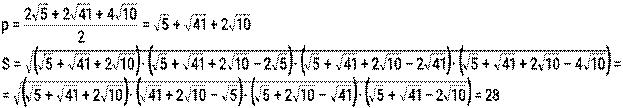
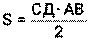 , значит
, значит 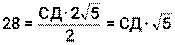
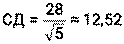
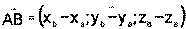
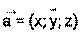 вычисляется по формуле
вычисляется по формуле 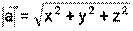
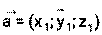 ,
, 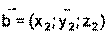 , то
, то 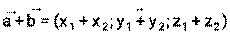
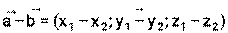
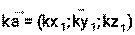
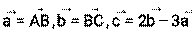 и длину вектора
и длину вектора 
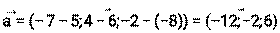
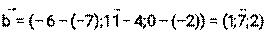
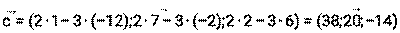
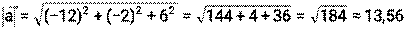
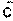 может быть разложен по двум перпендикулярным осям. В этом случае составляющие вектора называют проекциями вектора на ось и вычисляют по формулам
может быть разложен по двум перпендикулярным осям. В этом случае составляющие вектора называют проекциями вектора на ось и вычисляют по формулам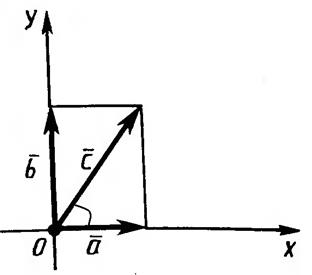
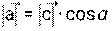
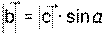
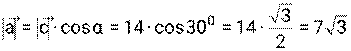
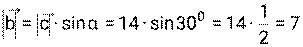
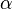
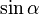


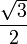
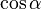
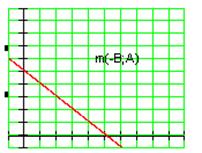

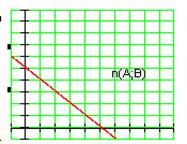

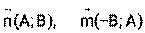 ).
).
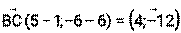 , значит –В=4, В= - 4, А=-12. Прямая ВС проходит через точку В, Значит С= - (-12∙1+(-4)∙6)= - (-36)=36.
, значит –В=4, В= - 4, А=-12. Прямая ВС проходит через точку В, Значит С= - (-12∙1+(-4)∙6)= - (-36)=36.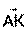 , точка К – середина стороны ВС
, точка К – середина стороны ВС 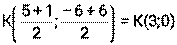 , значит
, значит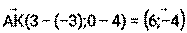 , отсюда –В=6, В= - 6, А= - 4. Прямая АК проходит через
, отсюда –В=6, В= - 6, А= - 4. Прямая АК проходит через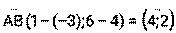 , значит –В= 4, В= - 4, А = 2. Прямая КМ проходит через
, значит –В= 4, В= - 4, А = 2. Прямая КМ проходит через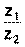
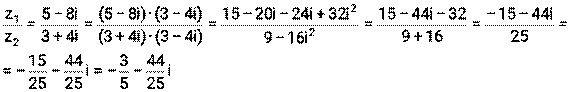
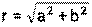 .
.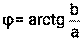 , если z находится в первой или четвёртой четвертях, или по формуле
, если z находится в первой или четвёртой четвертях, или по формуле 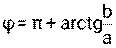 , если z находится во второй или третьей четвертях. При этом следует помнить, что
, если z находится во второй или третьей четвертях. При этом следует помнить, что 
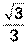
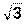
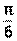
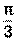
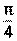
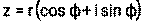 или в показательной форме:
или в показательной форме: 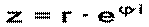
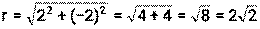
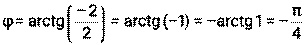
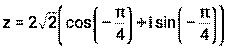
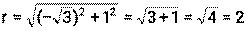
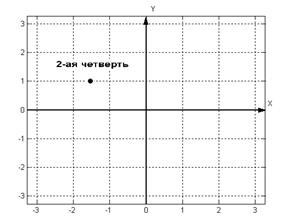
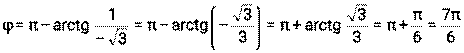
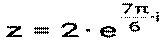
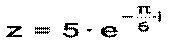 запишите в алгебраической форме
запишите в алгебраической форме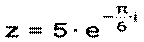 =
= 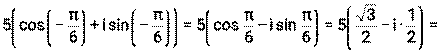
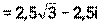
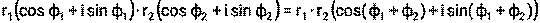
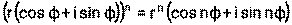
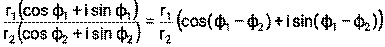
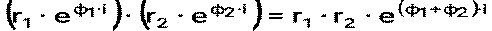
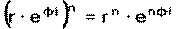
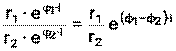
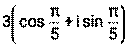 , z2=
, z2= 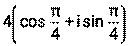 вычислить
вычислить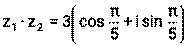 ∙
∙ 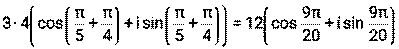
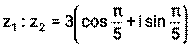 :
: 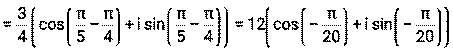
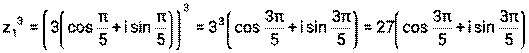
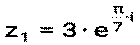 ,
, 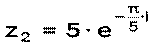 вычислить
вычислить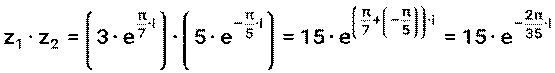
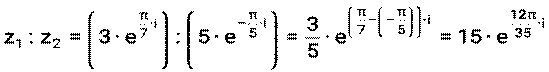
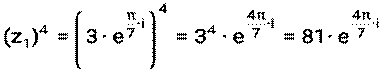
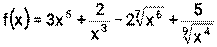 ;
;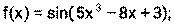
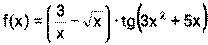 ;
;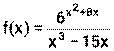 .
.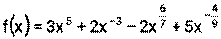 .
.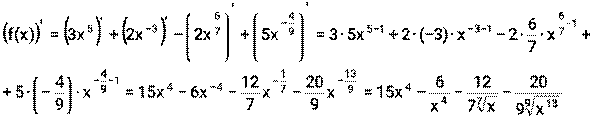
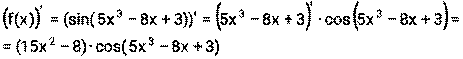
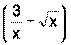 и
и , поэтому надо воспользоваться формулой (2)
, поэтому надо воспользоваться формулой (2)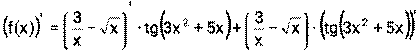
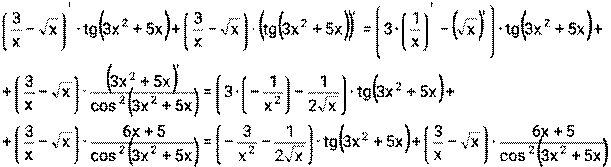
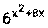 и
и , поэтому надо воспользоваться формулой (4)
, поэтому надо воспользоваться формулой (4)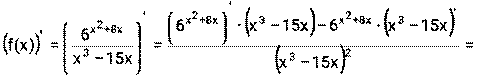
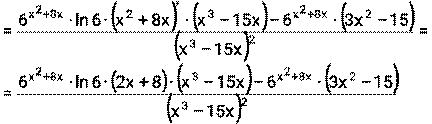
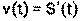
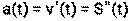
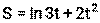 , где S – путь (м ), t- время (с). Найти скорость и ускорение тела в момент времени t=1с.
, где S – путь (м ), t- время (с). Найти скорость и ускорение тела в момент времени t=1с.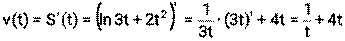
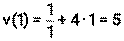 (м/с)
(м/с)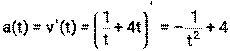
 (м/с2)
(м/с2)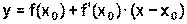
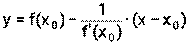
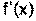 =2х+6
=2х+6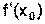 =
= 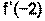 =2(-2)+6=2
=2(-2)+6=2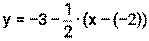
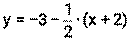
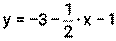
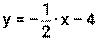
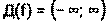 .
.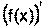 =(3х2-х3)=6х-3х2=3х(2-х)
=(3х2-х3)=6х-3х2=3х(2-х)


