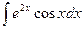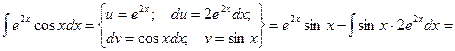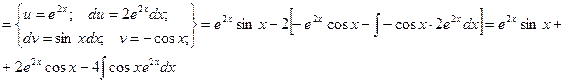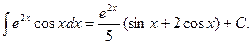Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие неопределенного интеграла
Функция F (x) называется первообразной от функции f (x) на отрезке [ a; b ], если во всех точках этого отрезка выполняется равенство: F ′(x) = f (x). Если функция F (x) является первообразной для функции f (x), то выражение F (x) + C называется неопределенным интегралом от функции f (x) и обозначается: ∫ f (x) dx. Свойства неопределенного интеграла: 1) (ò f (x) dx)′ = f (x) 2) ò a∙f(x)dx=a∙ ò f(x)dx (a=const) 3) ò (f(x) ±g(x))dx = ò f(x)dx ± ò g(x)dx.
Таблица основных интегралов
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Табличные значения производных основных функций 1. (un)' = n × un - 1 × u ' (n Î R) 2. (au)' = au × lna × u' 3. (eu)' = eu × u' 4.(log a u)' = 5. (ln u)' = 6. (sin u)' = cos u × u' 7. (cos u)' = - sin u × u' 8. (tg u)' = 9. (ctg u)' = - 10. (arcsin u)' = 11. (arccos u)' = - 12. (arctg u)' = 13. (arcctg u)' = - Методы интегрирования Непосредственное интегрирование
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы. Пример 1. Решение. Для вычисления интеграла сначала воспользовались 2 и 3 свойствами неопределенного интеграла, а затем применили 4, 1 и 10 табличные интегралы. Пример 2. Пример 3.
Метод замены переменной (метод подстановки)
Этот метод является одним из наиболее эффективных и распространенных приемов интегрирования, позволяющих во многих случаях упростить вычисление интеграла. Суть этого метода состоит в том, что путем введения новой переменной интегрирования заданный интеграл сводится к новому интегралу, который легко вычисляется непосредственным интегрированием.
Пример 4. Вычислить: ∫ (2 x +3)5 dx Решение. Введем новую переменную t = 2 x + 3, тогда dt = t ′ ∙ dx = (2 x +3)′ ∙ dx = 2 dx, откуда dx = ∫(2 x +3)5 dx = ∫ t 5 ∙ Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение (2 x +3) и получим окончательный ответ: ∫(2 x +3)5 dx =
Пример 5. Вычислить:
Решение. Введем новую переменную t = 5+ ex, dt = (5+ ex)′∙ dx = ex ∙ dx, dx =
Интегрирование по частям
Этот метод применяется, когда подынтегральная функция имеет вид:
где u и dv выбираются в соответствии с правилами:
1. Если 2. Если 3. Интегралы вида
Пример 6. Вычислить Решение. Данный интеграл относится к 1 типу. Положим
Пример 7. Вычислить Решение. Данный интеграл относится ко 2 типу. Выполним замену:
Пример 8. Вычислить Решение. Данный интеграл относится к 1 типу. Выполним замену:
(Получили интеграл, который решается интегрированием по частям. Выполним замену еще раз:
Пример 9. Вычислить
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
Практическое занятие №18 Наименование занятия: Интегрирование рациональных функций Цель занятия: Научиться вычислять неопределенные интегралы от рациональных функций. Формировать ОК-1, ОК-2, ОК-3, ОК-4, ОК-5, ОК-6, ОК-7, овладеть знаниями и умениями, необходимыми для освоения ПК-1.1, ПК-1.2 (спец. 09.02.03), ПК-1.1, ПК-1.2 (спец. 09.02.04) Подготовка к занятию: Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной» Литература:
Задание на занятие:
|
||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.221.113 (0.016 с.) |
 , (n ≠ -1)
, (n ≠ -1)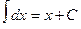



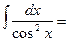 tg x + C
tg x + C -ctg x+ C
-ctg x+ C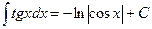


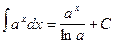
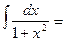 arctg x +C
arctg x +C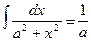 arctg
arctg 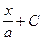
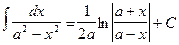
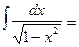 arcsin x + C
arcsin x + C arcsin
arcsin 
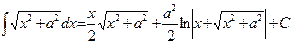

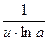 × u'
× u'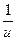 × u '
× u '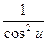 × u'
× u'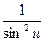 × u'
× u' × u'
× u' × u'
× u'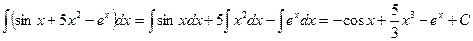
 .
.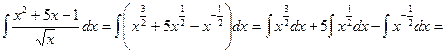
 .
. . Подставим новую переменную в интеграл (вместо выражения 2 x + 3 подставим t, вместо dx подставим
. Подставим новую переменную в интеграл (вместо выражения 2 x + 3 подставим t, вместо dx подставим 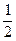 ∙∫ t 5 dt =
∙∫ t 5 dt = 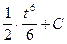 =
= 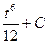 .
.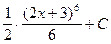 =
= 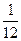 (2 x +3)6 + С.
(2 x +3)6 + С.
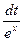 . Подставим новую переменную в интеграл:
. Подставим новую переменную в интеграл: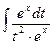 =
=  =
= 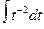 =
= 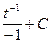 = -
= - 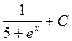
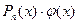 , где
, где 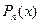 - это многочлен степени п, а
- это многочлен степени п, а  является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией. Формула метода:
является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией. Формула метода: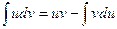 ,
,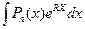 ,
,  ,
, 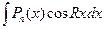 ), то для того чтобы найти эти интегралы, нужно сделать замену
), то для того чтобы найти эти интегралы, нужно сделать замену 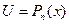
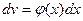 и применить формулу интегрирования по частям.
и применить формулу интегрирования по частям. ,
, 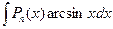 ,
, 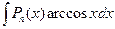 ,
, 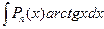 ,
, 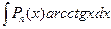 ) то для того, чтобы найти эти интегралы нужно сделать замену:
) то для того, чтобы найти эти интегралы нужно сделать замену:  ,
, 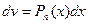 .
.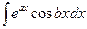 ,
, 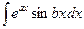 (a, b — числа) вычисляются двукратным интегрированием по частям.
(a, b — числа) вычисляются двукратным интегрированием по частям.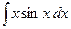 .
.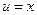 ,
, 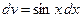 ; тогда
; тогда 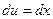 ,
, 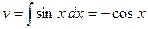 . Подставим в формулу интегрирования по частям:
. Подставим в формулу интегрирования по частям: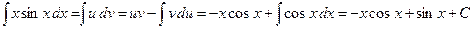 .
.
 ,
, 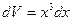 ,
,  ,
, 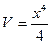
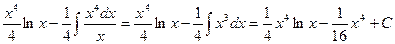

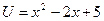 ,
, 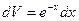 ,
,  ,
, 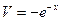
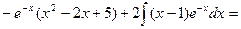
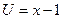 ,
,  ,
, 
 .
.