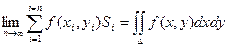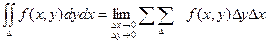Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные функций нескольких переменных
Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение D х к переменной х. Тогда величина D x z = f (x + D x, y) – f (x, y) называется частным приращением функции по х. Можно записать
Тогда Обозначается: Аналогично определяется частная производная функции по у.
Пример 1. Найти частные производные функции
Пример 2. Найдем частные производные функции
Полное приращение и полный дифференциал Выражение
Полным дифференциалом функции z = f(x, y) называется главная линейная относительно D х и D у приращения функции D z в точке (х, у).
Для функции произвольного числа переменных:
Пример 3. Найти полный дифференциал функции
Пример 4. Найти полный дифференциал функции
Практическое занятие №24 Наименование занятия: Вычисление двойных интегралов Цель занятия: Научиться вычислять двойные интегралы. Формировать ОК-2, ОК-5. Подготовка к занятию: Повторить теоретический материал по теме «Интегральное исчисление функции нескольких действительных переменных». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Двойные интегралы
Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0.
0 x
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называться незамкнутой область ю D. С геометрической точки зрения D - площадь фигуры, ограниченной контуром. Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние D х i, а по оси у – на D у i. Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны Si = D xi × D yi. В каждой частичной области возьмем произвольную точку Р(х i, yi) и составим интегральную сумму
где f – функция непрерывная и однозначная для всех точек области D. Если бесконечно увеличивать количество частичных областей D i, тогда площадь каждого частичного участка Si стремится к нулю. Если при стремлении к нулю шага разбиения области D интегральные суммы
С учетом того, что Si = D xi × D yi получаем:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.12.170 (0.015 с.) |
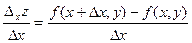 .
.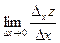 называется частной производной функции z = f(x, y) по х.
называется частной производной функции z = f(x, y) по х.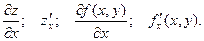
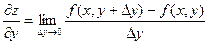
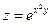 .
. ,
, 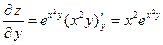 .
.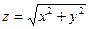 :
: .
.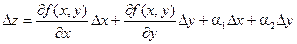 называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при D х ® 0 и D у ® 0 соответственно.
называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при D х ® 0 и D у ® 0 соответственно.
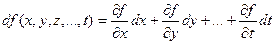
 .
.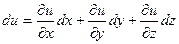
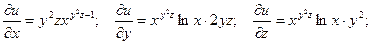
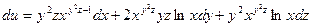

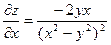

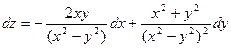

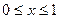

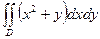
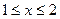
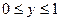

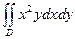
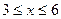

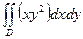
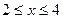
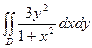

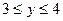
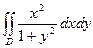
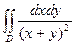

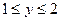
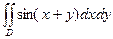
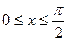


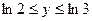
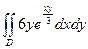
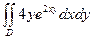
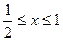

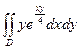
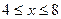
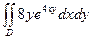


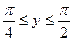
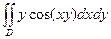
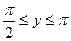

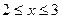

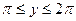


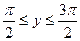
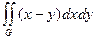 G: x = 0, y = 0, x + y = 2
G: x = 0, y = 0, x + y = 2
 G: x = 1, y = х 2, y =
G: x = 1, y = х 2, y = 
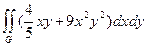 G: x = 1, y = - х 3, y =
G: x = 1, y = - х 3, y = 
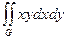 G: y = 0, y = x, х = 1
G: y = 0, y = x, х = 1
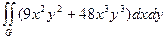 G: x = 1, y = - х 2, y =
G: x = 1, y = - х 2, y =  G: x = 1, y = х 3, y =
G: x = 1, y = х 3, y = 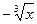
 G: x = 1, y = х 3, y =
G: x = 1, y = х 3, y = 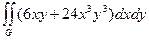 G: x = 1, y = - х 2, y =
G: x = 1, y = - х 2, y =  G: y = х 3, x = 0, x + y = 2
G: y = х 3, x = 0, x + y = 2
 G: x = 1, y = - х 3, y =
G: x = 1, y = - х 3, y = 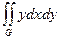 G: y = 0, y = cos x, y = x + 1
G: y = 0, y = cos x, y = x + 1
 G: x = 1, y = х 2, y =
G: x = 1, y = х 2, y = 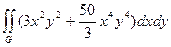 G: x = 1, y = - х 2, y =
G: x = 1, y = - х 2, y = 
 y
y
 имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.