
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.
Общее решение:
Линейные неоднородные дифференциальные уравнения
Для интегрирования линейных неоднородных уравнений (Q(x) ¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа. Метод Бернулли Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций При этом
Подставляя в исходное уравнение, получаем:
Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению. Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение Таким образом, можно получить функцию u, проинтегрировав полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение
Интегрируя, можем найти функцию v:
Т.е. была получена вторая составляющая произведения Подставляя полученные значения, получаем:
Окончательно получаем формулу:
где С2 - произвольный коэффициент.
Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
Пример 1. Решить уравнение Решение. Сначала приведем данное уравнение к стандартному виду: Применим полученную выше формулу:
Пример 2. Решить уравнение
Решение. Разделим уравнение на xy2: Полагаем
Полагаем
Произведя обратную подстановку, получаем:
Практическое занятие №28 Наименование занятия: Решение дифференциальных уравнений высших порядков
Цель занятия: Научиться решать дифференциальные уравнения 2-го порядка. Формировать ОК-2, ОК-6, ОК-8. Подготовка к занятию: Повторить теоретический материал по теме «Обыкновенные дифференциальные уравнения». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие:
Вариант 2 |
Вариант 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 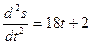 ,
если ,
если 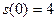 , , 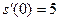
|
если |
если | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 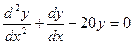 ,
если ,
если 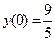 , , 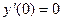
|
если |
если | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 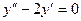 ,
если ,
если 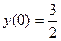 , , 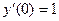
|
если |
если | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 4 |
Вариант 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Дать определение дифференциального уравнения второго порядка.
- Как решаются дифференциальные уравнения, допускающие понижение степеней?
- Записать схему решения линейных однородных и неоднородных уравнений 2-го порядка с постоянными коэффициентами.
ПРИЛОЖЕНИЕ
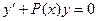 .
.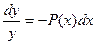 ;
; 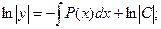
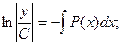
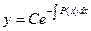
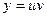 .
.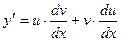 - дифференцирование по частям.
- дифференцирование по частям.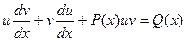
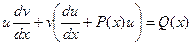
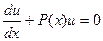 .
.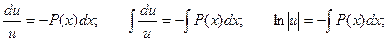
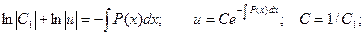
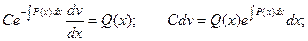
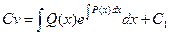 ;
;  ;
;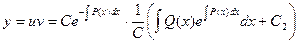
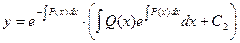 ,
, 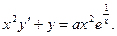
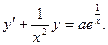
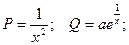
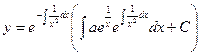
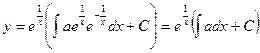
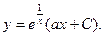
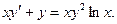

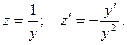
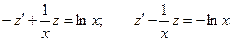 .
.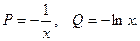
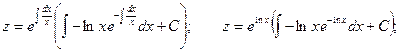
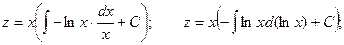
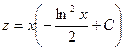
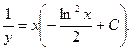
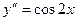
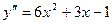
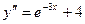
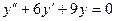
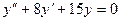
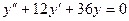
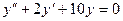
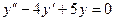
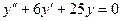
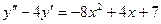
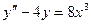
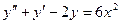

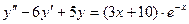
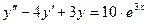
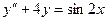
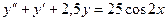
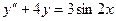


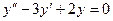
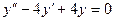
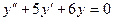
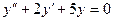
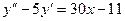
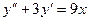
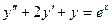
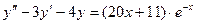
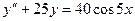
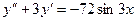
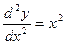 ,
,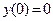 ,
, 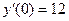
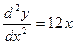 ,
,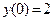 ,
, 
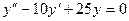 ,
,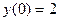 ,
, 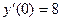
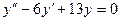 ,
,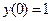 ,
, 
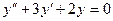 ,
,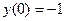 ,
, 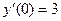
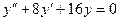 ,
,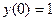 ,
, 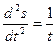 , если
, если 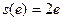 ,
, 
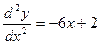 , если
, если 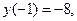
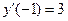
 если у (0) = 4, у′ (0) = -4
если у (0) = 4, у′ (0) = -4 если
если 


