
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и условная сходимость рядов⇐ ПредыдущаяСтр 16 из 16
Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд (2), составленный из модулей его членов. Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают. Пример 9. Исследовать на сходимость ряд Решение. Ряд удовлетворяет условиям признака Лейбница, т.к.
Ряд, составленный из модулей его членов
Ряд (1) называется условно сходящимся, если он сходится, а ряд (2), составленный из модулей его членов, расходится. Пример 10. Исследовать на сходимость ряд Решение. Ряд удовлетворяет условиям признака Лейбница, т.к.
Признаки Даламбера и Коши для знакопеременных рядов
Пусть дан знакопеременный ряд. Признак Даламбера. Если существует предел Признак Коши. Если существует предел
Практическое занятие №30 Наименование занятия: Нахождение области сходимости степенного ряда. Разложение элементарных функций в ряд Маклорена Цель занятия: Научиться находить область сходимости степенных рядов, раскладывать элементарные функции в ряд Маклорена. Формировать ОК-1, ОК-2, ОК-5, ОК-9, овладеть знаниями и умениями, необходимыми для освоения ПК-1.2 (спец. 09.02.03), ПК-1.2 (спец. 09.02.04). Подготовка к занятию: Повторить теоретический материал по теме «Теория рядов». Литература:
Задание на занятие: Найти области сходимости степенных рядов
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Степенные ряды
Степенным рядом называется ряд вида
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример 1. Исследовать на сходимость ряд Решение. Применяем признак Даламбера:
Получаем, что этот ряд сходится при Теперь определим сходимость в граничных точках –1 и 1. При х = –1 получим ряд: При х = 1 получим ряд: Теорема Абеля. Если степенной ряд Следствие. Если при х = х 1 ряд расходится, то он расходится для всех
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
Пример 2. Найти область сходимости ряда Решение. Находим радиус сходимости ряда
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
Теорема. Если степенной ряд
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.237.122 (0.009 с.) |

 и
и 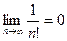 , то данный ряд сходится.
, то данный ряд сходится.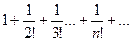 , по признаку Даламбера сходится, следовательно, данный ряд является абсолютно сходящимся.
, по признаку Даламбера сходится, следовательно, данный ряд является абсолютно сходящимся.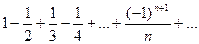
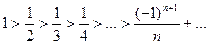 и
и 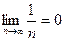 , то данный ряд сходится. Рассмотрим ряд, составленный из модулей его членов:
, то данный ряд сходится. Рассмотрим ряд, составленный из модулей его членов: 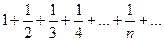 Это гармонический ряд, который расходится. Следовательно, данный ряд является условно сходящимся.
Это гармонический ряд, который расходится. Следовательно, данный ряд является условно сходящимся. , то при r<1 данный ряд будет абсолютно сходящимся, а при r>1 - расходящимся. При r=1 признак не дает ответа о сходимости ряда.
, то при r<1 данный ряд будет абсолютно сходящимся, а при r>1 - расходящимся. При r=1 признак не дает ответа о сходимости ряда.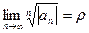 , то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
, то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.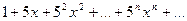
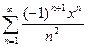
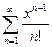
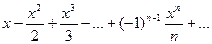
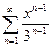

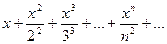
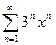
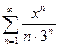

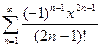

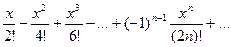
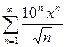
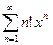

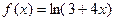
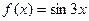
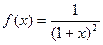


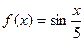
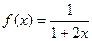
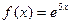
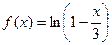


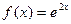
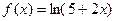
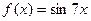
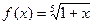




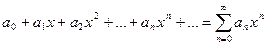 .
.
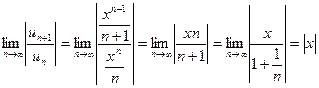 .
.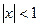 и расходится при
и расходится при 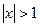 .
.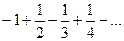 Данный ряд сходится по признаку Лейбница
Данный ряд сходится по признаку Лейбница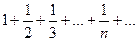 Данный ряд расходится (гармонический ряд).
Данный ряд расходится (гармонический ряд). .
. ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех 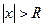 ряд расходится. При этом число R называется радиусом сходимости. Интервал (- R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (- R, R) называется интервалом сходимости.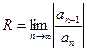
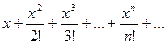
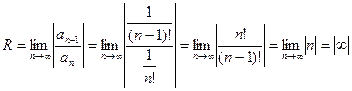 .
.
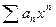 сходится для положительного значения х = х 1, то он сходится равномерно в любом промежутке внутри
сходится для положительного значения х = х 1, то он сходится равномерно в любом промежутке внутри  .
.


