Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование случайной величины, распределённой по заданному законуПостроение гистограммы распределения
Дана функция (2.1), в которой необходимо сначала определить неизвестный коэффициент, а затем вычислить функцию распределения.
f(x)=b(3-x), b>0, 1<x<2, (2.1)
Для этих вычислений воспользуемся методом обратной функции. Для вычисления неизвестного коэффициента (параметра) воспользуемся проверкой условия нормировки (2.2):
Подставив данную для исследований функцию, получаем:
Прировняв полученное выражение к единице, находим параметр b:
b=2/3 (2.4)
Подставив найденный параметр в начальную функцию, получаем:
Далее необходимо вычислить функцию распределения
где u – случайная величина, распределённая на отрезке [0;1] x1 – нижний предел функции f(x) Для функции (2.1) получаем:
При решении уравнения (2.7) получаем неопределённость:
Для выбора искомой функции, необходимо проверить принадлежность х интервалу (1;2) при крайних значениях u. После проверки один вариант функции (2.8) отсеялся, функция (2.8) приняла вид:
Получили закон распределения
Тогда за теоретическую плотность распределения принимается функция (2.5). Остальные вычисления аналогичны первому разделу. Количество интервалов в гистограмме, определенное по правилу Стургерса:
Промежуточные вычисления для построения гистограммы определяются как в предыдущем разделе:
где
n – объём выборки
Из способа построения гистограммы следует, что полная площадь всех прямоугольников равна единице:
где fs(x) - эмпирическая плотность распределения (полученная экспериментально), которую можно вычислить по формуле:
На полученную гистограмму для качественного анализа необходимо наложить теоретическую плотность распределения случайной величины, распределенной по закону:
В итоге получится гистограмма распределения (см. график 2) с отображением эмпирической и теоретической плотностей распределения, которая даёт возможность наглядно сравнить эти плотности.
График 2 – Сравнение эмпирической и теоретической плотностей распределения
Определение выборочной оценки математического ожидания и дисперсии
Вычисление выборочного среднего производиться по формуле (2.11):
Тогда выборочную дисперсию можно рассчитать по следующей формуле (2.12):
Для дисперсии в качестве несмещенной и состоятельной оценки используется величина (2.13):
Теоретические значения математического ожидания и дисперсии вычисляются по формулам (2.14-2.15):
Теоретические значения должны попадать в доверительные интервалы.
|
||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 45; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.132 (0.004 с.) |
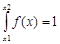 (2.2)
(2.2)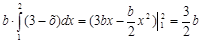 , (2.3)
, (2.3)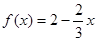 (2.5)
(2.5)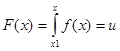 (2.6)
(2.6)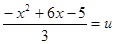 (2.7)
(2.7)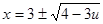 (2.8)
(2.8)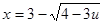 (2.9)
(2.9)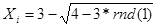 .
.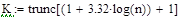 ,
, 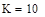 .
.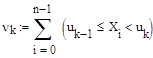 (2.6)
(2.6)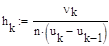 (2.7)
(2.7)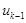 и
и 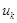 - границы интервала,
- границы интервала,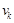 - частота попадания выборочных величин в интервал (
- частота попадания выборочных величин в интервал (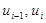 )
)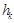 - высота прямоугольника на графике
- высота прямоугольника на графике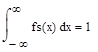 (2.8)
(2.8)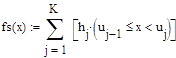 (2.9)
(2.9)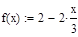 (2.10)
(2.10)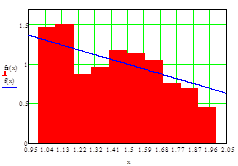
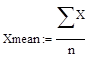
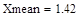 (2.11)
(2.11)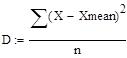
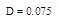 (2.12)
(2.12)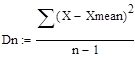 (2.13)
(2.13)
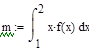 (2.14)
(2.14)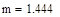
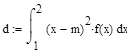 (2.15)
(2.15)