Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение гистограммы распределения
Для получения реализации последовательности независимых случайных величин с произвольным распределением используют реализации последовательности независимых случайных величин равномерно распределенных на отрезке [0,1]. Случайные равномерно распределенные величины генерируются специальной программой, входящей в математическое обеспечение компьютера, и называемой датчиком случайных чисел. При моделировании нормально распределенной случайной величины на основе равномерно распределенных величин чаще всего используется центральная предельная теорема: Пусть 1) случайная величина
2) случайная величина
На основании центральной предельной теоремы рассмотрим сумму
где Известно, что каждая из случайных величин
Тогда согласно теоремам сложения математических ожиданий и дисперсий
Следовательно, случайная величина (1.5) имеет математическое ожидание
В данной работе дано количество слагаемых в сумме N, задано математическое ожидание
Гистограмма распределения представляет собой удобный способ представления статистических данных. Гистограмма строится следующим образом: Пусть имеется выборка случайной величины объемом n:
При данных условиях
При данных условиях Весь отрезок [A,B] разбивается на K интервалов, как правило, одинаковой длины. Число интервалов при построении гистограммы не должно быть слишком большим и слишком малым. При большом количестве интервалов в гистограмме обнаруживаются незакономерные колебания. На практике рекомендуется в каждом интервале иметь не менее 5-10 точек. Предварительный выбор количества интервалов можно сделать по правилу Стургенса:
где n – объём выборки,
Найдя количество интервалов разбиения, можно вычислить длину каждого интервала по формуле:
Для построения гистограммы нужно частоту попадания случайных величин xk в каждый интервал [
где
n – объём выборки
Из способа построения гистограммы следует, что полная площадь всех прямоугольников равна единице:
где fs(x) - эмпирическая плотность распределения (полученная экспериментально), которую можно вычислить по формуле:
На полученную гистограмму для качественного анализа необходимо наложить теоретическую плотность распределения случайной величины, распределенной по закону
В итоге получится гистограмма распределения (см. график 1) с отображением эмпирической и теоретической плотностей распределения, которая даёт возможность наглядно сравнить эти плотности.
График 1 – Сравнение эмпирической и теоретической плотностей распределения
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.78.106 (0.009 с.) |
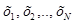 последовательность взаимно независимых случайных величин, имеющих одно и то же распределение вероятностей с конечным математическим ожиданием
последовательность взаимно независимых случайных величин, имеющих одно и то же распределение вероятностей с конечным математическим ожиданием 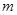 . Тогда при
. Тогда при 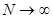 имеем:
имеем: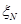 , вычисляемая по формуле (1.1), сходится по вероятности к
, вычисляемая по формуле (1.1), сходится по вероятности к 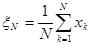 (1.1)
(1.1)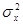 величин
величин 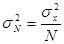 (1.2)
(1.2)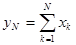 ,
,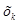 с распределением R[0,1] имеет математическое ожидание (1.3) и дисперсию (1.4).
с распределением R[0,1] имеет математическое ожидание (1.3) и дисперсию (1.4).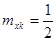 (1.3)
(1.3)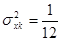 (1.4)
(1.4)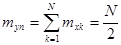 ,
,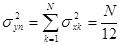 .
.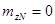 и дисперсию
и дисперсию 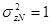 и при
и при 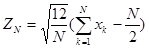 (1.5)
(1.5)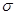 выходной случайной величины y. Если известна случайная величина с распределением N[0,1], то случайная величина с распределением N[
выходной случайной величины y. Если известна случайная величина с распределением N[0,1], то случайная величина с распределением N[ 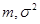 ] получается в результате линейного преобразования
] получается в результате линейного преобразования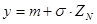 (1.6)
(1.6)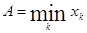 (1.7)
(1.7)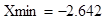
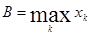 (1.8)
(1.8)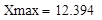
 (1.9)
(1.9)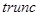 () – операция взятия целой части от действительного числа Если число точек в интервале слишком мало (порядка 1-2), то имеет смысл объединить некоторые интервалы и пересчитать гистограмму.
() – операция взятия целой части от действительного числа Если число точек в интервале слишком мало (порядка 1-2), то имеет смысл объединить некоторые интервалы и пересчитать гистограмму.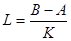 или
или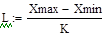 (1.10)
(1.10)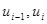 ) разделить на его длину
) разделить на его длину 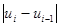 и полученную величину взять в качестве высоты прямоугольника на графике. Причем последний интервал необходимо рассмотреть как отрезок. Таким образом, описанное правило можно изобразить математически:
и полученную величину взять в качестве высоты прямоугольника на графике. Причем последний интервал необходимо рассмотреть как отрезок. Таким образом, описанное правило можно изобразить математически: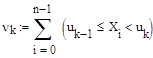 (1.11)
(1.11)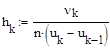 (1.12)
(1.12)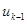 и
и 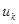 - границы интервала,
- границы интервала, - частота попадания выборочных величин в интервал (
- частота попадания выборочных величин в интервал (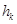 - высота прямоугольника на графике
- высота прямоугольника на графике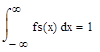 (1.13)
(1.13)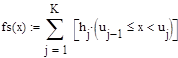 (1.14)
(1.14)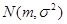
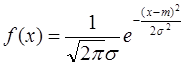 (1.15)
(1.15)