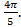Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление длины дуги кривой, заданной в полярных координатах. ⇐ ПредыдущаяСтр 7 из 7
Длина дуги кривой вычисляется по формуле
Предположим, что
Замечание: В практических примерах при нахождении длины дуги, как правило, не нужно строить чертеж. Иллюстрация приведена только для некоторых примеров (для наглядности).
Пример 5.8. Найти длину дуги кривой: а)
Решение. а) Уравнение Для этого найдем
Тогда б)
=
Замечание: В случаи симметричной фигуры заданной параметрически или в полярных координатах необходимо найти часть длины дуги, иначе мы можем прийти к противоречию -нулевому результату(поскольку работаем с тригонометрическими функциями), покажем это на примере в).
в) для этого найдем
1способ: (Найдем
2 способ: (найдем Заметим, что фигура симметрична относительно координатных осей, поэтому для начала найдем
следовательно г) Кардиоида
5.3. Вычисление объемов тел вращения Представьте некоторую плоскую фигуру на координатной плоскости. Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами: вокруг оси абсцисс, вокруг оси ординат. В данном разделе будут разобраны оба случая. Рассмотрим кривую, заданную уравнением
Так как, каждое сечение этого тела плоскостью,перпендикулярной оси
Итак объем тела, полученного вращением вокруг оси
Замечание: В практических заданиях плоская фигура иногда может располагаться и ниже оси (
Аналогично размышляя,получим формулу
Объём кольца, образованного вращением вокруг оси плоской фигуры, ограниченной непрерывными неотрицательными на
Замечание: Если вращается криволинейной трапеции вокруг оси
Пример 5.9. Вычислить объем тела, полученного вращением вокруг оси Решение.
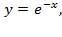
Объем тела вращения вычисляем по формуле
Решение.
На рис.24, плоская фигура заштрихована, именно она и вращается вокруг оси
Замечание: Пределы интегрирования по оси следует расставлять строго снизу вверх. Пример 5.11. Вычислить объем тела, полученного вращением вокруг оси Решение.
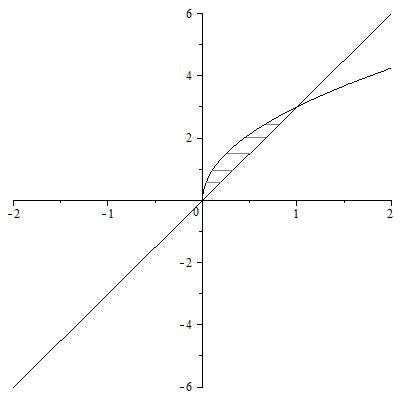
Для построения чертежа плоской фигуры найдем точки пересечения параболы
Следовательно, имеется две точки пересечения (0;0), (1;3), отмечаем данные точки на чертеже и через точки пересечения проводим кривые. Кривые в пересечении образуют область заключенную между линиями
В итоге искомый объём равен:
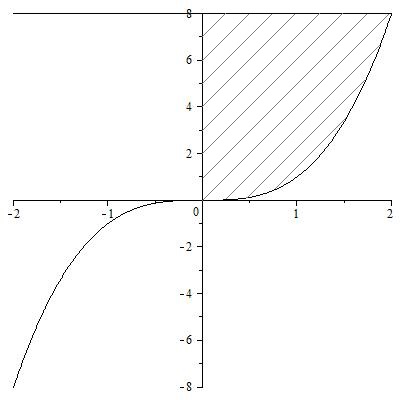
Пример 5.12. Вычислить объем тела, образованного вращением вокруг оси
Решение. Выполним чертеж, для этого найдем точки пересечения заданных линий:
При При
Итак, имеется две точки пересечения (1;1), (-1;1), отмечаем данные точки, при этом заметим, что функции
Для нахождения объема тела вращения достаточно использовать правую половину фигуры, так как полученная фигура симметрична относительно начала координат. Таким образом, заштрихованная правая часть, вращаясь вокруг оси Перейдем к обратным функциям, то есть, выразим Аналогично для
Таким образом,
Задания для самостоятельного решения 13. Вычислить площадь фигуры, ограниченной линиями:
Ответы: 13. 1. 13. 23. 14. Вычислить длину дуги линии:
Ответы:
14. 1. 14. 12. 14. 17. 15. Найти объем тела, полученного вращением плоской фигуры, ограниченной линиями:
Ответы: 15.1. 15.16.
Литература 1. Б.В.Соболь, Н. Т. Мишняков, В.М. Поркшеян, Практикум по высшей математике.3-е изд. Ростов н \ Д:Феникс, 2010. 2. Д.Т.Письменный, Конспект лекций по высшей математике (полный курс). 2-е изд. Москва: «Айрис-пресс», 2014. 3. Данко П.Е., Попов, А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах (1 том). — М.: Высш. шк., 2002.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.125 (0.065 с.) |
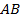 заданной в полярных координатах уравнением
заданной в полярных координатах уравнением 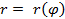 ,
, 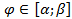
 (5.12)
(5.12) 
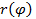 и
и 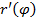 непрерывны на отрезке
непрерывны на отрезке 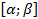 .Если в равенствах связывающих полярные и декартовы координаты
.Если в равенствах связывающих полярные и декартовы координаты 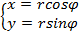 ,угол
,угол 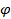 считать параметром,то кривую
считать параметром,то кривую 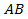 можно задать параметрически
можно задать параметрически 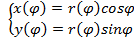 ,тогда
,тогда 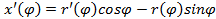 ,
,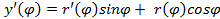 , применяем формулу (5.9) для нахождения длины дуги имеем:
, применяем формулу (5.9) для нахождения длины дуги имеем: 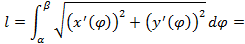
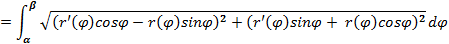
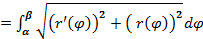 , где
, где 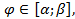 что и требовалось показать.
что и требовалось показать.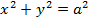 ;б)
;б) 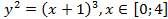 ;в)
;в) 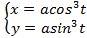
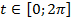 ;г)
;г) 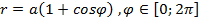 .
.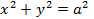 задаёт окружность,с центром в начале координат и радиусом
задаёт окружность,с центром в начале координат и радиусом 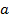 в декартовой системе координат, поэтому длину её дуги будем вычислять по формуле (5.8),поскольку она симметрично задана,достаточно вычислить четвертую часть длины дуги
в декартовой системе координат, поэтому длину её дуги будем вычислять по формуле (5.8),поскольку она симметрично задана,достаточно вычислить четвертую часть длины дуги 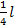
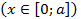 и результат умножить на четыре.
и результат умножить на четыре.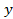 из уравнения
из уравнения 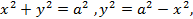
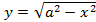 и
и 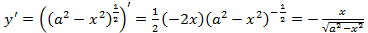 и подставим в формулу (5.8):
и подставим в формулу (5.8):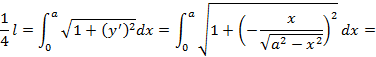
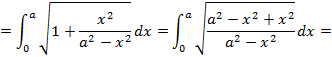
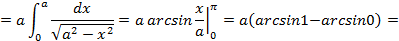
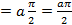 .
.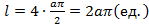 , получили общеизвестную формулу длины окружности, формулу для вычисления длины дуги окружности с центром в начале координат произвольного радиуса. Если в данном примере положить
, получили общеизвестную формулу длины окружности, формулу для вычисления длины дуги окружности с центром в начале координат произвольного радиуса. Если в данном примере положить 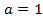 ,получим окружность с единичным радиусом, длина дуги которой будет равна
,получим окружность с единичным радиусом, длина дуги которой будет равна 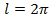 . При различных значениях параметра
. При различных значениях параметра 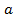 (радиуса)длина окружности будет изменяться;
(радиуса)длина окружности будет изменяться;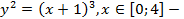 кривая задана в декартовых координатах, поэтому найдем
кривая задана в декартовых координатах, поэтому найдем 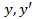 и подставим в формулу(5.8):
и подставим в формулу(5.8):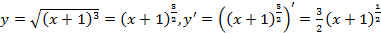 ,
,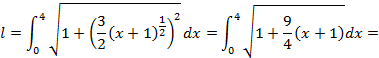
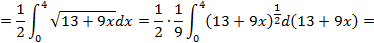
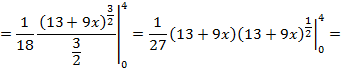
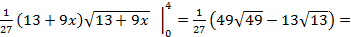
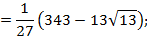
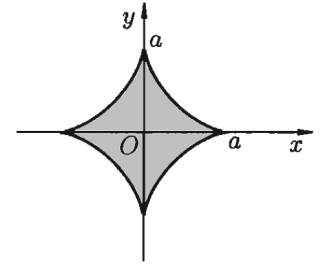
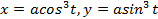 - это кривая называется астроида (рис.20) задана параметрически, поэтому длину дуги будем находить по формуле (5.10),
- это кривая называется астроида (рис.20) задана параметрически, поэтому длину дуги будем находить по формуле (5.10),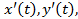
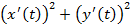 , и подставим в формулу:
, и подставим в формулу: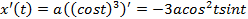 ,
,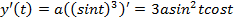
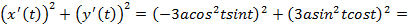
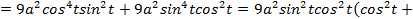
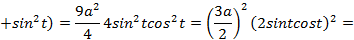
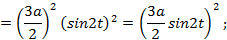
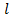 ,
, 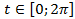 ;)
;) 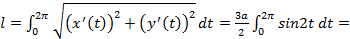
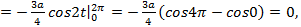 пришли к противоречию;
пришли к противоречию;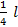 ,
, 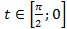 )
)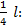
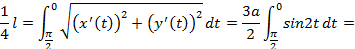
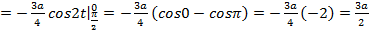 ,
,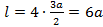 ;
;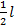 , для этого вычислим
, для этого вычислим 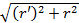 , и подставим в формулу (5.12):
, и подставим в формулу (5.12):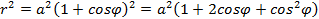 ,
,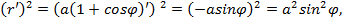
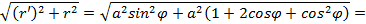
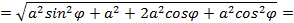
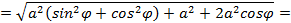
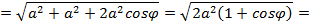
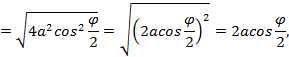


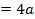 , отсюда
, отсюда 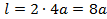 .
.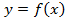 . Предположим, что функция
. Предположим, что функция 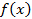 непрерывна на отрезке
непрерывна на отрезке 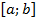 . Если соответствующую ей криволинейную трапецию с основаниями
. Если соответствующую ей криволинейную трапецию с основаниями 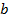 вращать вокруг оси
вращать вокруг оси 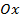 ,то получим так называемое тело вращения.
,то получим так называемое тело вращения.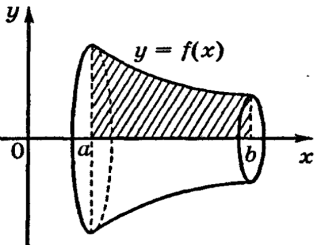
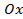 ,то есть плоскостью
,то есть плоскостью  , представляет собой круг радиуса
, представляет собой круг радиуса 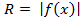 ,c площадью
,c площадью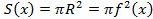 ,то объем тела вращения может быть найден по формуле
,то объем тела вращения может быть найден по формуле 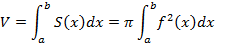
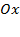 криволинейной трапеции, ограниченной линиями
криволинейной трапеции, ограниченной линиями 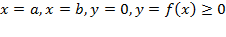 (рис.21),вычисляется по формуле
(рис.21),вычисляется по формуле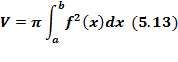
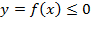 ).Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат
).Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат 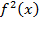 (интеграл всегда неотрицателен).
(интеграл всегда неотрицателен).
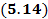 для вычисления объема тела, полученного вращением вокруг оси
для вычисления объема тела, полученного вращением вокруг оси  криволинейной трапеции, ограниченной линиями
криволинейной трапеции, ограниченной линиями 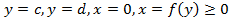 (рис. 22.),
(рис. 22.),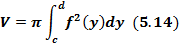
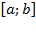 функциями
функциями 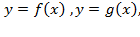
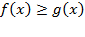 , и прямыми
, и прямыми 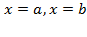 вычисляется по формуле
вычисляется по формуле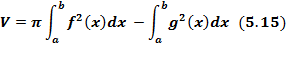
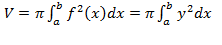 подставляем параметрические функции
подставляем параметрические функции 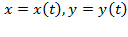 , а также соответствующие пределы интегрирования
, а также соответствующие пределы интегрирования 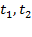 :
: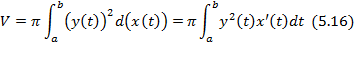
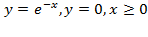 .
.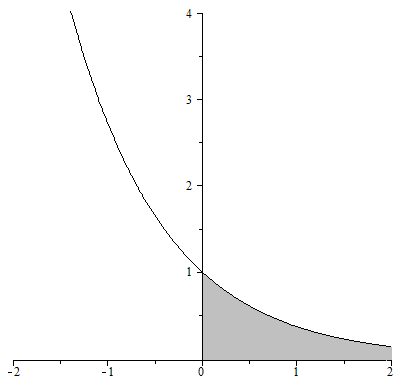
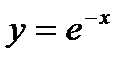
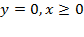 .Искомая плоская фигура заштрихована(рис.23), именно она и вращается вокруг оси
.Искомая плоская фигура заштрихована(рис.23), именно она и вращается вокруг оси 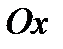 . В результате вращения получается воронка, которая симметрична относительно оси
. В результате вращения получается воронка, которая симметрична относительно оси 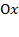 .
.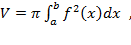 в нашем случае
в нашем случае 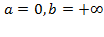 ,
,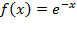 ,так как плоская фигура ограничена графиком экспоненты
,так как плоская фигура ограничена графиком экспоненты 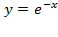 сверху. В итоге искомый объем равен:
сверху. В итоге искомый объем равен: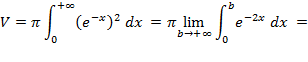
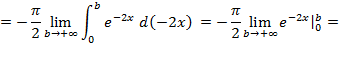
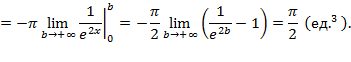
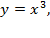
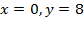 , вокруг оси
, вокруг оси  .
.
 . Так как, фигура вращается вокруг оси
. Так как, фигура вращается вокруг оси 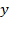 применяя формулу
применяя формулу 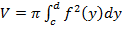 ,в нашем случае
,в нашем случае 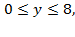 то есть
то есть 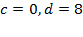 ,
, 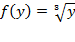 ,действительно, если выразить
,действительно, если выразить  через
через 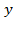 получим
получим 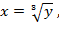 подставляя в формулу находим объем:
подставляя в формулу находим объем: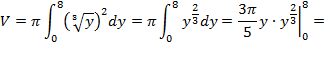
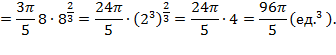
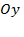
 .
.
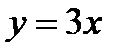
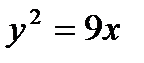
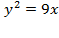 с вершиной в начале координат симметричной относительно оси
с вершиной в начале координат симметричной относительно оси 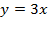 проходящей через начало координат решив уравнение:
проходящей через начало координат решив уравнение: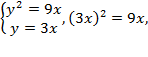
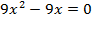 ,
, 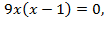
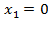 ,
, 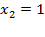
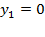 ,
, 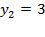 .
.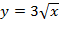 (ветвь параболы
(ветвь параболы 
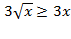 ,поэтому объем находим как разность объёмов
,поэтому объем находим как разность объёмов 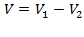 ,где
,где 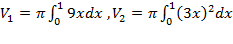 .
.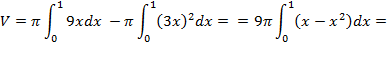
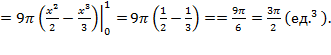
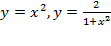 .
.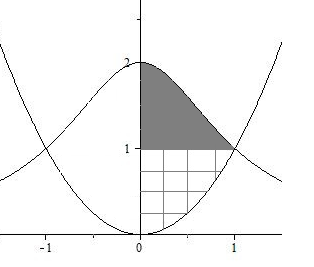
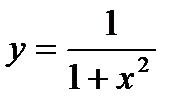
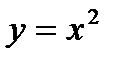
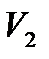
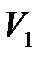
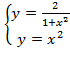 ,
,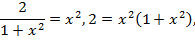
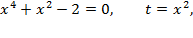
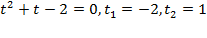
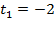 ,
, 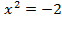 - вещественных корней нет;
- вещественных корней нет;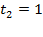 ,
, 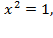
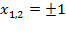 ,тогда
,тогда 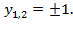
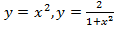 чётные, то есть симметричны относительно начала координат. Заметим, что функция
чётные, то есть симметричны относительно начала координат. Заметим, что функция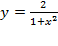 пересекает ось
пересекает ось 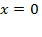 ,
, 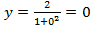 .
.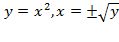 . Обратите внимание, что правой ветви параболы
. Обратите внимание, что правой ветви параболы 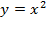 соответствует обратная функция
соответствует обратная функция 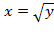 ,а левой (неиспользуемой) ветви параболы соответствует обратная функция
,а левой (неиспользуемой) ветви параболы соответствует обратная функция 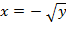 .
.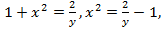
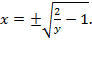 Объем тела вращения необходимо искать по формуле (5.13) как сумму объемов тел вращений:
Объем тела вращения необходимо искать по формуле (5.13) как сумму объемов тел вращений: 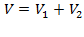 ,где
,где 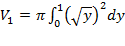 ,так как на отрезке
,так как на отрезке 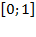 расположен график функции
расположен график функции 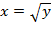 ;
;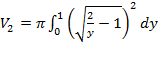 , так как на отрезке
, так как на отрезке 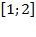 расположен график функции
расположен график функции 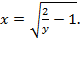
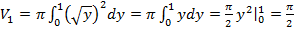 ;
;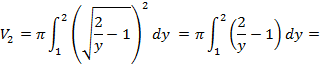
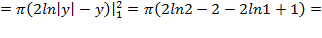
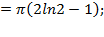
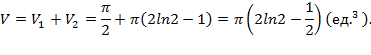
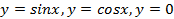
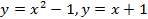
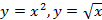
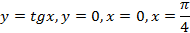
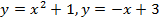
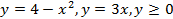
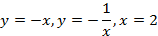
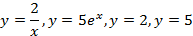
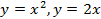
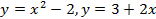
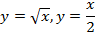
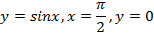
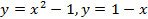
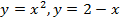
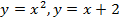
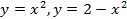

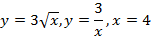
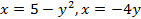
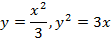
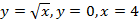
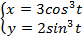
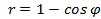
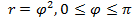
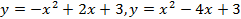
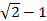 ; 13.2.
; 13.2. 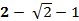 ; 13.3.
; 13.3. 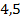 ; 13.4.
; 13.4.  ; 13.5.
; 13.5. 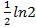 13.6.
13.6. 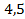 ; 13.7.
; 13.7. 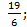 13. 8.
13. 8. 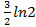 ; 13.9.
; 13.9. 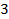 ; 13.10.
; 13.10.  . 13.11.
. 13.11. 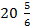 ; 13.12.
; 13.12. 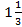 : 13.13. 1; 13.14. 4,5; 13.15.
: 13.13. 1; 13.14. 4,5; 13.15.  ; 13.16. 4,5; 13.17.
; 13.16. 4,5; 13.17. 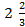 ; 13.18.
; 13.18. 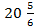 ; 13.19.
; 13.19. 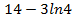 ; 13.20. 30; 13.21. 3; 13.22.
; 13.20. 30; 13.21. 3; 13.22. 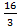 ;
;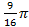 ; 13.24.
; 13.24. 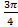 ; 13. 25.
; 13. 25. 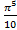 ; 13.26.
; 13.26. 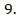








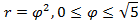
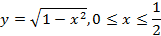
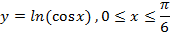
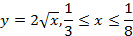

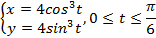
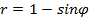 ,
, 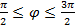
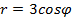 ,
, 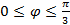
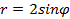 ,
, 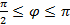
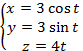 ,
, 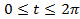
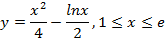

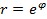 ,
, 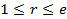
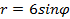 ,
, 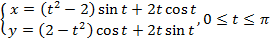

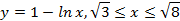
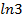 ; 14. 2.
; 14. 2. 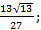 14. 3.
14. 3. 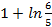 ; 14. 4. 8; 14. 5.
; 14. 4. 8; 14. 5. 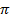 ; 14. 6.
; 14. 6.  ; 14. 7.
; 14. 7. 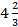 ; 14. 8. 2; 14. 9. 2; 14. 10.
; 14. 8. 2; 14. 9. 2; 14. 10. 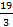 ; 14. 11.
; 14. 11. 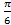 ;
;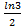 ; 14. 13.
; 14. 13. 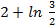 ; 14. 14.
; 14. 14. 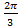 ; 14. 15.
; 14. 15. 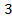 ; 14. 16. 2;
; 14. 16. 2;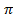 ; 14. 18.
; 14. 18. 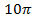 ; 14. 20.
; 14. 20. 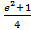 ; 14. 21.
; 14. 21. 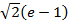 ; 14. 22.
; 14. 22. 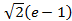 ; 14. 23.
; 14. 23. 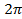 ; 14. 24.
; 14. 24. 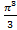 ; 14. 25.
; 14. 25. 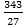 ; 14. 26.
; 14. 26. 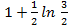 .
.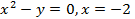 (вокруг оси
(вокруг оси 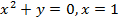 (вокруг оси
(вокруг оси 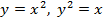 (вокруг оси
(вокруг оси 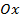 );
);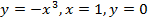 (вокруг оси
(вокруг оси 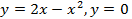 (вокруг оси
(вокруг оси 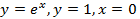 (вокруг оси
(вокруг оси 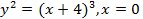 (вокруг оси
(вокруг оси 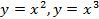 ; (вокруг оси
; (вокруг оси 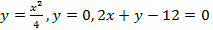 (вокруг оси
(вокруг оси 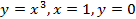 (вокруг оси
(вокруг оси 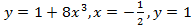 (вокруг оси
(вокруг оси 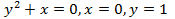 (вокруг оси
(вокруг оси  (вокруг оси
(вокруг оси 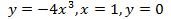 (вокруг оси
(вокруг оси 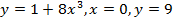 (вокруг оси
(вокруг оси  (вокруг оси
(вокруг оси 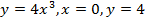 (вокруг оси
(вокруг оси 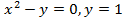 (вокруг оси
(вокруг оси 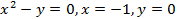 (вокруг оси
(вокруг оси 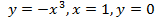 (вокруг оси
(вокруг оси 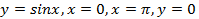 (вокруг оси
(вокруг оси 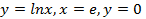 (вокруг оси
(вокруг оси 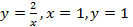 (вокруг оси
(вокруг оси 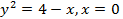 (вокруг оси
(вокруг оси 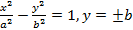 (вокруг оси
(вокруг оси 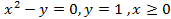 (вокруг оси
(вокруг оси 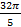 ; 15.2.
; 15.2.  ; 15.3.
; 15.3. 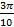 ; 15.4.
; 15.4. 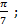 15.5.
15.5. 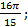 15.6.
15.6. 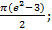 15.7.
15.7. 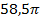 ; 15.8.
; 15.8. 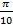 ; 15.9.
; 15.9. 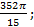 15.10.
15.10. 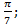 15.11.
15.11. 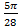 ; 15.12.
; 15.12. 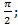 15.13.
15.13. 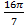 ; 15.15.
; 15.15. 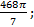
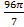 ; 15.18.
; 15.18. 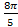 ; 15.19.
; 15.19. 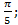 15.20.
15.20. 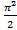 ; 15.22.
; 15.22. 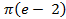 ; 15.23.
; 15.23. 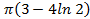 ; 15.24.
; 15.24. 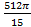 ; 15.25.
; 15.25. 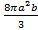 ; 15.26.
; 15.26.