
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Р азложение правильной рациональной дроби на сумму простейших.
Теорема 3.1: Всякую правильную рациональную дробь а) Каждому неповторяющемуся множителю вида б) Каждому неповторяющемуся множителю вида
в) Каждому неповторяющемуся множителю вида
г) Каждому неповторяющемуся множителю вида
Постоянные Теорема 3.2: Всякую неправильную рациональную дробь
Интегрировать простейшей дроби мы уже умеем. Рассмотрим, как проинтегрировать рациональную дробь, которая не является элементарной. Правило (интегрирования рациональных дробей): 1) Если подынтегральная дробь неправильная, то ее необходимо представить в виде суммы многочлена 2) Раскладываем знаменатель правильной дроби а) Сумму всех простейших дробей привести к общему знаменателю; б) Числитель получившейся дроби приравнять числителю исходной дроби. в)Найти коэффициенты одним из методов: методом приравнивания коэффициентов -приравнять коэффициенты при одинаковых степенях многочленов в левой и правой частях равенства, полученную систему уравнений решить относительно неизвестных коэффициентов, входящих в числители простейших дробей; либо методом произвольных значений- в уравнение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных вещественных значений
3) Простейшие дроби интегрируют по отдельности с помощью соответствующих методов их интегрирования.
Пример 3.7. Представить дробь Решение. Представлена правильная рациональная дробь, так как
Правую часть приведем к общему знаменателю:
Так как две дроби с одинаковыми знаменателями равны, то тождественно равны их числители:
Найдем коэффициенты 1 c пособ (метод произвольных значений)- находим
Следовательно, 2 способ (метод неопределенных коэффициентов) - раскрываем скобки в уравнении
Числа, обозначенные большими буквами
Решим полученную систему
Итого, Пример 3.8. Вычислить интеграл Решение. 1)Под знаком интеграла правильная рациональная дробь 2)Разложим знаменатель дроби на множители, для этого вынесем за скобки
уравнение
Получим систему
3)Возвращаясь к исходному интегралу, получим:
Проинтегрируем отдельно простейшую рациональную дробь третьего вида
Итого,
Замечание: Для упрощения решения системы, состоящей из коэффициентов, иногда полезно группировать два метода нахождения коэффициентов, рассмотренных выше. Как это сделать рассмотрим на примере 3.9. Пример 3.9. Вычислить интеграл Решение. 1)Так как, дробь неправильная(
2)Осталось проинтегрировать правильную дробь
В соответствии с теоремой 2.1. в) получим разложение на простейшие дроби:
Применяя для начала метод произвольных значений, полагая
Оставшиеся коэффициенты данным методом найти не получается (решение будет довольно громоздким), для их нахождения, применим метод неопределенных коэффициентов, раскрываем скобки в последнем уравнении и приравниваем коэффициенты при одинаковых степенях имеем:
Подставляя
3)Возвращаясь, к правильной дроби, получим:
В итоге, получим:
Пример 3.10. Вычислить Решение. 1)Дробь под знаком интеграла является правильной, так как 2) Разложим знаменатель дроби
имеем вещественный корень
Переходя к общему знаменателю и приравнивая числители, имеем:
Находим коэффициенты
Зная
3)Возвращаясь к исходному интегралу, получим:
3.2. Интегрирование тригонометрических функций. Интегралы вида Здесь Интегралы вида
В результате исходное выражение приводится к интегралу от рациональной функции переменной
Замечание: Универсальная подстановка весьма громоздка, поэтому на практике применяют и другие более простые подстановки, в зависимости от вида подынтегральной функции, позволяющие рационализировать исходный интеграл.
Рассмотрим различные виды интегральных функции и запишем соответствующие им подстановки: 1) Подынтегральная функция нечетная относительно В частности, интегралы вида
2) Подынтегральная функция нечетная относительно В частности, интегралы вида
3) Функция под знаком интеграла четная относительно
Для данной подстановки имеем:
Таким образом:
В частности, при вычислении интегралов вида
Замечание: Иногда при интегрировании тригонометрических функций данного вида (четных относительно 4) Интегралы произведения синусов и косинусовразличных аргументов
5) Для интегралов вида
Пример 3.11. Вычислить интеграл: б) е) з) Решение. а)Так как подынтегральная функция
б) Так как, подынтегральная функция
в)Под знаком интеграла четная относительно
г)Функция под знаком интеграла чётная относительно
д)
е) Преобразовывая произведение синусов в разность косинусов
ё)Так как подынтегральная функция
ж)
з)Интеграл имеет вид
и) й) Подынтегральная функция общего вида (ни чётная, ни нечётная),то есть не обладает ни одним из перечисленных выше свойств, поэтому применяем универсальную подстановку
к) Аналогично, применяем универсальную подстановку:
3.3. Интегрирование некоторых иррациональных функций. Перед тем как находить интеграл от иррациональной функции, вспомним ее определение. Функция называется иррациональной, если переменная величина находится под знаком корня. Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой, может быть найден как известно всегда. Рассмотрим подстановки для интегрирования различных типов иррациональных функций: 1) Рассмотрим интеграл
Подстановка, рационализирующая подынтегральную функцию имеет вид: чисел
Пример 3.12. Вычислить интеграл Решение. Переходя от корня к степени имеем:
Замечание: Аналогично рационализируются интегралы вида Пример 3.13. Найти интеграл Решение. Переходя от корня к степени имеем:
2) Интегралы вида а) Для
б)
в) Пример 3.14. Вычислить интеграл Решение. Интеграл имеет вид
=
Пример 3.15. Вычислить интеграл Решение. Интеграл имеет вид
=
3) Интегралы вида Правило: Выделяем полный квадрат в квадратном трехчлене
Пример 3.16. Вычислить интеграл Решение. Преобразуем подынтегральную функцию выделяя полный квадрат под корнем:
Заметим, что интеграл имеет вид
3.4. «Берущиеся» и «не берущиеся» интегралы. Как уже отмечалось выше, операция интегрирования функций значительно сложнее операции дифференцирования функций. Не всегда выбранный путь интегрирования является наилучшим, более коротким, простым. Интегрирование часто может быть выполнено не единственным способом. Многое зависит от знания рекомендуемых искусственных приемов интегрирования и от практических навыков решения интегралов. Пример 3.17. Вычислить Решение.
Пример 3.18. Вычислить Решение. Вряд ли стоит вычислять интеграл раскладывая подынтегральную функцию на простейшие дроби:
Заметив, что числитель
Рассмотренные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл. Говорят, что Не могут быть выражены через элементарные функции следующие интегралы (так как не существует элементарной функции, производная от которой была бы равна подынтегральному выражению): 1) 2) 3) 4) 5) Замечание: Первообразные от функций 1)-5), хорошо изучены, для них составлены подробные таблицы значений для различных значений аргумента. Задания для самостоятельного решения 7. а) Найти интегралы от правильных рациональных дробей:
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.152.162 (0.281 с.) |
||||||||||||||||||||||||
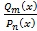 можно представить единственным образом, в виде суммы простейших дробей типов 1) — 4) этом:
можно представить единственным образом, в виде суммы простейших дробей типов 1) — 4) этом: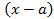 в разложении знаменателя правильной рациональной дроби соответствует одна простейшая дробь вида
в разложении знаменателя правильной рациональной дроби соответствует одна простейшая дробь вида 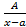 ;
;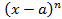 в разложении знаменателя правильной рациональной дроби соответствует сумма простейших дробей
в разложении знаменателя правильной рациональной дроби соответствует сумма простейших дробей ;
;
 в разложении знаменателя правильной рациональной дроби соответствует одна простейшая дробь вида
в разложении знаменателя правильной рациональной дроби соответствует одна простейшая дробь вида 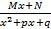 ;
; в разложении знаменателя правильной рациональной дроби соответствует сумма простейших дробей
в разложении знаменателя правильной рациональной дроби соответствует сумма простейших дробей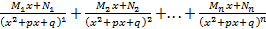 .
.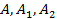 ,…,
,…, 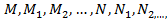 называют неопределенными коэффициентами.
называют неопределенными коэффициентами. ,можно разложить, и притом единственным образом, на сумму многочлена
,можно разложить, и притом единственным образом, на сумму многочлена 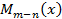 и правильной рациональной дроби
и правильной рациональной дроби 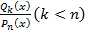 :
: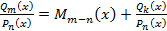 ,где
,где 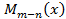 -целая часть,
-целая часть, 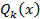 - остаток от деления
- остаток от деления 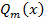 на
на 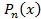 .
.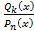 (разделив
(разделив 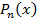 уголком, из неё выделяют целую часть
уголком, из неё выделяют целую часть 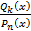
 ;
;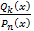 на множители и представляем ее в виде суммы простейших дробей. Правильную рациональную дробь
на множители и представляем ее в виде суммы простейших дробей. Правильную рациональную дробь  ,…,
,…, 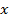 и находят коэффициенты(в качестве произвольных значений принимаются точки при которых знаменатель обращается в ноль);
и находят коэффициенты(в качестве произвольных значений принимаются точки при которых знаменатель обращается в ноль);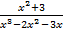 в виде суммы простейших дробей.
в виде суммы простейших дробей.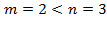 ,разложим её знаменатель на множители
,разложим её знаменатель на множители  . Получим первый корень
. Получим первый корень 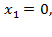 для разложения квадратного трёхчлена в скобках решим квадратное уравнение:
для разложения квадратного трёхчлена в скобках решим квадратное уравнение: 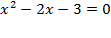
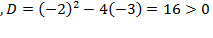 ,
,  , то есть имеем дело со случаем, когда многочлен
, то есть имеем дело со случаем, когда многочлен 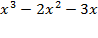 имеет простые действительные корни
имеет простые действительные корни 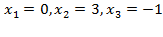 , следовательно разложение знаменателя на множители имеет вид:
, следовательно разложение знаменателя на множители имеет вид: 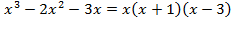 . Разложение исходной дроби в соответствии с теоремой 3.1.а) будет следующим:
. Разложение исходной дроби в соответствии с теоремой 3.1.а) будет следующим: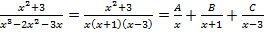 ;
; ;
;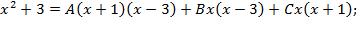
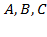 двумя способами:
двумя способами:  при которых знаменатель дроби равен нулю, подставляя их значения поочередно в левую и правую часть полученного равенства, имеем:
при которых знаменатель дроби равен нулю, подставляя их значения поочередно в левую и правую часть полученного равенства, имеем:
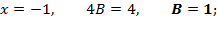

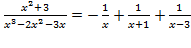 ;
;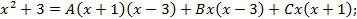
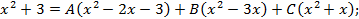
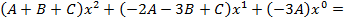

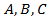 -коэффициенты, пока неизвестны. Находим их методом неопределенных коэффициентов, приравнивая коэффициенты при одинаковых степенях
-коэффициенты, пока неизвестны. Находим их методом неопределенных коэффициентов, приравнивая коэффициенты при одинаковых степенях  :
: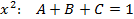
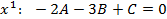
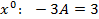
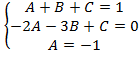 ,чтобы исключить
,чтобы исключить  из первого уравнения, вычтем из него второе уравнение и найдем
из первого уравнения, вычтем из него второе уравнение и найдем 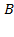 :
: 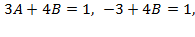
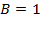 .Подставляя в первое уравнение
.Подставляя в первое уравнение 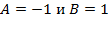 найдем
найдем 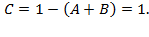
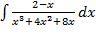 .
. ,поэтому переходим к следующему этапу;
,поэтому переходим к следующему этапу;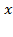 ,а затем найдем корни квадратного уравнения в скобках:
,а затем найдем корни квадратного уравнения в скобках: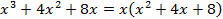 ,
,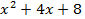 не имеет вещественных корней, так как
не имеет вещественных корней, так как 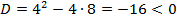 , то есть имеем дело со случаем, когда многочлен в знаменателе имеет комплексно-сопряженные корни. Оба сомножителя
, то есть имеем дело со случаем, когда многочлен в знаменателе имеет комплексно-сопряженные корни. Оба сомножителя  , переходя к общему знаменателю получим,
, переходя к общему знаменателю получим, 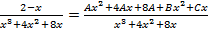 , приравнивая числители имеем:
, приравнивая числители имеем: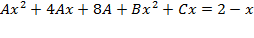 ;
;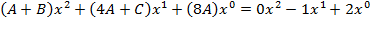 ;
;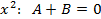
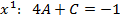
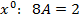
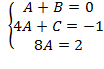 , решая её найдём
, решая её найдём 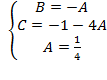 ;
;  ;
;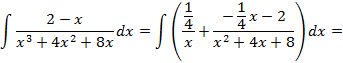

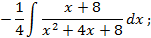
 ,используя метод замены переменной:
,используя метод замены переменной:
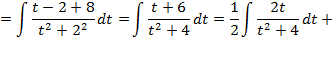
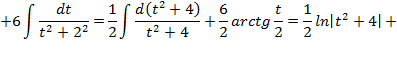
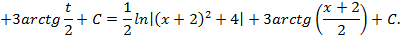
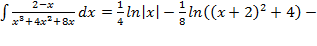
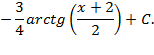
 .
.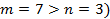 , то предварительно следует, выделить у нее целую часть путем деления многочлена на многочлен «уголком»:
, то предварительно следует, выделить у нее целую часть путем деления многочлена на многочлен «уголком»: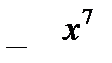
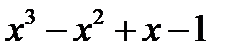
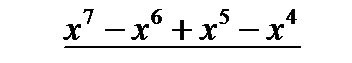


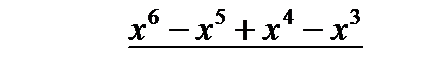

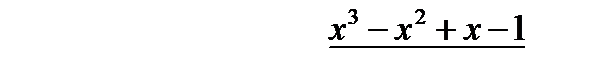
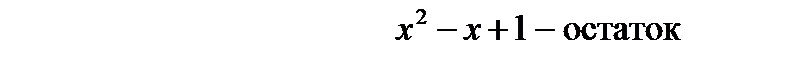
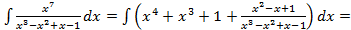
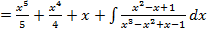 ;
; ,для этого разложим знаменатель полученной дроби на множители и найдем коэффициенты, комбинируя два способа нахождения коэффициентов:
,для этого разложим знаменатель полученной дроби на множители и найдем коэффициенты, комбинируя два способа нахождения коэффициентов: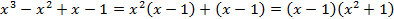 ,
,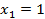 вещественный корень; уравнение
вещественный корень; уравнение 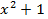 не имеет вещественных корней, действительно
не имеет вещественных корней, действительно  , то есть имеются комплексно-сопряженные корни.
, то есть имеются комплексно-сопряженные корни.
 +
+ 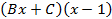
 в подчеркнутом уравнении, найдем
в подчеркнутом уравнении, найдем 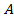 :
: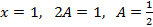 .
.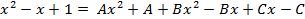 ;
; ;
;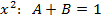
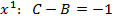

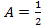 (найденное ранее методом частных значений)в полученную систему
(найденное ранее методом частных значений)в полученную систему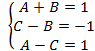 имеем:
имеем: 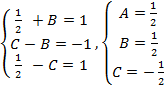 ,коэффициенты найдены;
,коэффициенты найдены;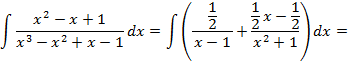

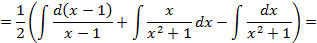
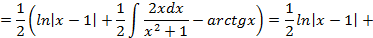
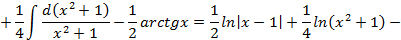
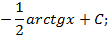
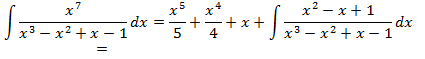
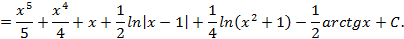
 .
.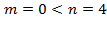 , поэтому переходим к следующему этапу;
, поэтому переходим к следующему этапу;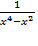 на множители:
на множители:
 (кратность корня) случай б) в теореме 3.1 и вещественные корни
(кратность корня) случай б) в теореме 3.1 и вещественные корни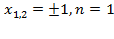 случай а) в теореме 3.1. Получим следующее разложение на простейшие дроби:
случай а) в теореме 3.1. Получим следующее разложение на простейшие дроби:
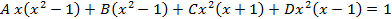 ;
; . В нашем случае (вещественном) для их нахождения, удобнее применить метод произвольных значений:
. В нашем случае (вещественном) для их нахождения, удобнее применить метод произвольных значений: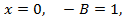

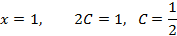
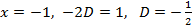 .
.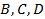 полагая, например,
полагая, например, 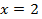 найдем
найдем 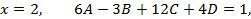
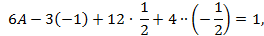
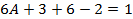 ,
,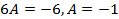 ;
;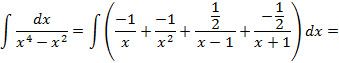
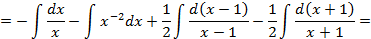
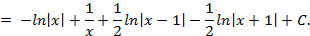
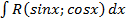 называются интегралами от тригонометрических функций.
называются интегралами от тригонометрических функций.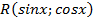 – обозначение некоторой функции от переменных
– обозначение некоторой функции от переменных 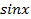 и
и 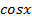 над которыми выполняются рациональные действия (сложение, вычитание, умножение и деление).
над которыми выполняются рациональные действия (сложение, вычитание, умножение и деление).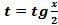 . Для данной подстановки имеем:
. Для данной подстановки имеем: 
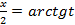 ,
, 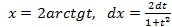 ,
,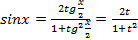 ,
, 
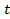 :
: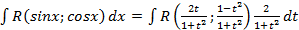 . А как интегрируются рациональные функции мы уже знаем (см. главу 3.1.)
. А как интегрируются рациональные функции мы уже знаем (см. главу 3.1.) , то есть
, то есть 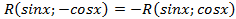 ,тогда интеграл
,тогда интеграл 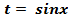 .
.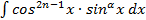 ,где
,где 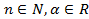 интегрируются аналогично, только при
интегрируются аналогично, только при 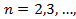 необходимо выделить множитель
необходимо выделить множитель .
.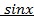 ,то есть
,то есть 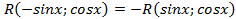 , то необходимо сделать подстановку
, то необходимо сделать подстановку 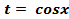 ,
,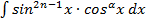 ,где
,где 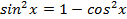 .
.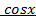 , то есть
, то есть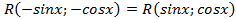 , тогда для преобразования подынтегральной функции в рациональную используется подстановка
, тогда для преобразования подынтегральной функции в рациональную используется подстановка 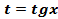 .
.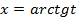 ,
, 
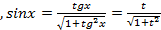 ,
, .
.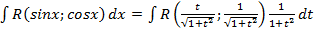 .
.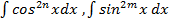 , где
, где 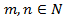 , удобнее применять формулы понижения степени:
, удобнее применять формулы понижения степени: 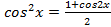 ,
, 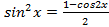 .
. ) удобно применить формулы
) удобно применить формулы  и
и 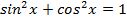 .
.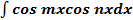 ,
, 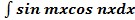 ,
,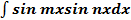 приводятся к табличным с помощью формул преобразования произведения синусов, косинусов в сумму (разность):
приводятся к табличным с помощью формул преобразования произведения синусов, косинусов в сумму (разность):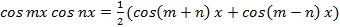 ;
;

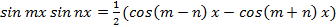 .
.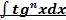 ,
, 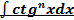 ,где
,где .Необходимо выделить множитель
.Необходимо выделить множитель 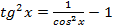 или
или  , в зависимости от вида подынтегральной функции.
, в зависимости от вида подынтегральной функции.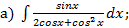
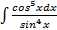 ; в)
; в) 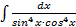 ; г)
; г)  ;д)
;д)  ;
; ; ё)
; ё) 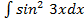 ; ж)
; ж)  ;
;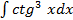 ; и)
; и) 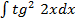 ; Й)
; Й) 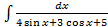 ;к)
;к) 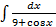 .
.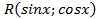 =
=  - нечетная относительно
- нечетная относительно 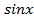 ,действительно,
,действительно, 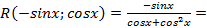
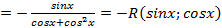 , поэтому делая подстановку
, поэтому делая подстановку 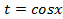 имеем:
имеем: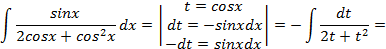
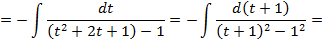
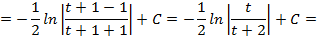
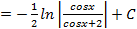 ;
;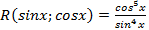 нечетная относительно косинуса,то есть
нечетная относительно косинуса,то есть 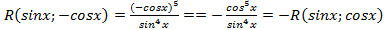 , при этом
, при этом 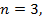 предварительно преобразовав подынтегральную функцию, выделив множитель
предварительно преобразовав подынтегральную функцию, выделив множитель  , а далее сделав подстановку
, а далее сделав подстановку 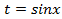 , имеем:
, имеем: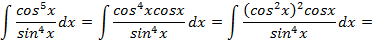
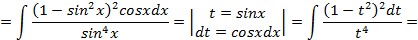

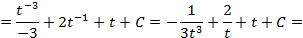
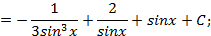
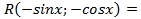
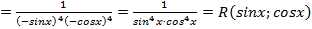 ,поэтому данное выражение рационализируется при помощи подстановки
,поэтому данное выражение рационализируется при помощи подстановки 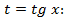
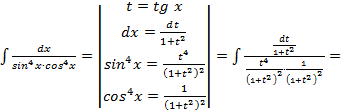
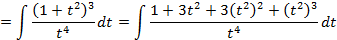
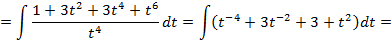
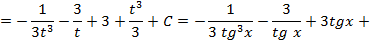
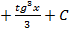 ;
;
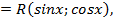 но здесь нет необходимости делать подстановку
но здесь нет необходимости делать подстановку 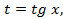 гораздо удобнее преобразовать подынтегральную функцию,
гораздо удобнее преобразовать подынтегральную функцию, 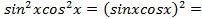
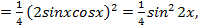 в итоге получим сводящийся к табличному интеграл:
в итоге получим сводящийся к табличному интеграл:
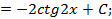
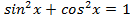 ,тогда имеем:
,тогда имеем:
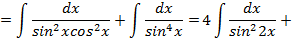
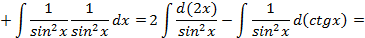


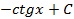 ;
;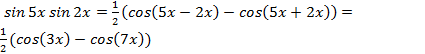 , получим:
, получим:
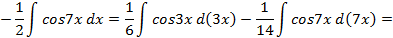

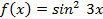 имеет вид
имеет вид 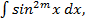 , где
, где  ,то применяя формулу понижения степени
,то применяя формулу понижения степени  ,получим:
,получим: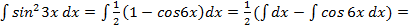
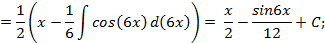
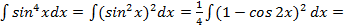
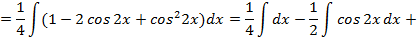
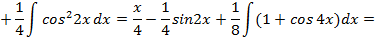
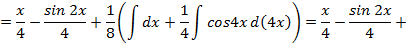
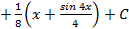 ;
;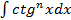 ,где
,где 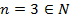 .Необходимо выделить множитель
.Необходимо выделить множитель 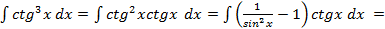
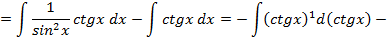

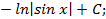
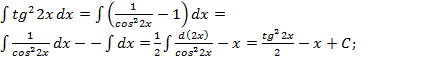
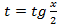 :
:
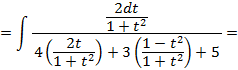

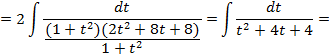
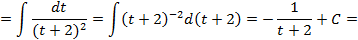
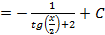 ;
;
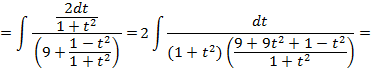
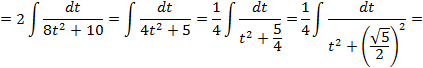

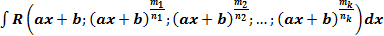 , где
, где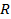 — рациональная функция,
— рациональная функция, 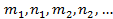 — целые числа.
— целые числа.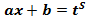 ,
,  где
где 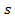 — наименьшее общее кратное (НОК)
— наименьшее общее кратное (НОК) , то есть, наименьшее натуральное число, делящееся нацело на
, то есть, наименьшее натуральное число, делящееся нацело на 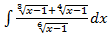 .
.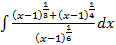 заметим,что
заметим,что 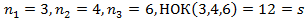 ,следовательно данное выражение рационализируется с помощью подстановки
,следовательно данное выражение рационализируется с помощью подстановки  :
: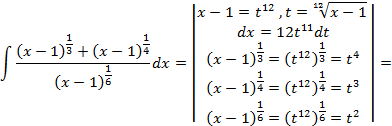
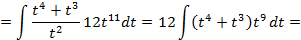
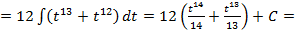
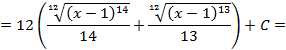

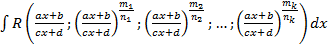 ,то есть при помощи подстановки
,то есть при помощи подстановки 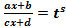 .
.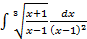
 заметим, что
заметим, что 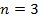 ,НОК(3)=3=s,следовательно данное выражение рационализируется с помощью подстановки
,НОК(3)=3=s,следовательно данное выражение рационализируется с помощью подстановки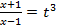 ,учитывая, что
,учитывая, что 
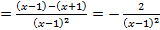 имеем:
имеем: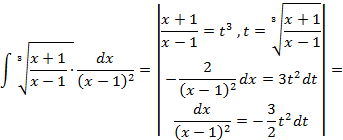
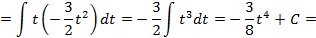
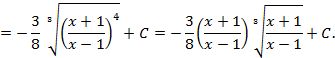
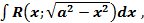
 рационализируются при помощи соответствующей тригонометрической подстановки:
рационализируются при помощи соответствующей тригонометрической подстановки:
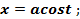
 подстановка
подстановка 
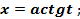
 подстановка
подстановка 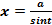 или
или 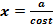 .
.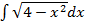 .
.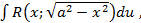 где
где  ,следовательно, интеграл рационализируется при помощи подстановки
,следовательно, интеграл рационализируется при помощи подстановки 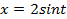 :
: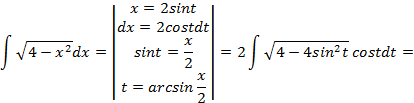
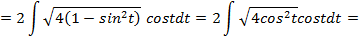

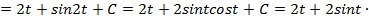
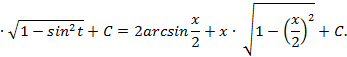
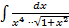 .
. ,где
,где  ,следовательно, интеграл рационализируется с помощью подстановки
,следовательно, интеграл рационализируется с помощью подстановки 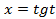 :
: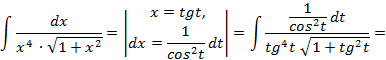
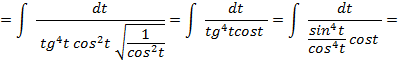
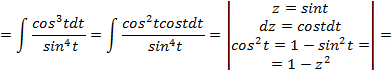


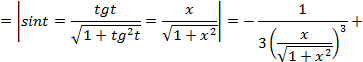

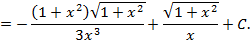
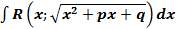 рационализируется по следующему правилу.
рационализируется по следующему правилу.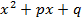 и вводим новую переменную
и вводим новую переменную 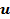 (выражение в скобках, выделенного квадрата),получим интеграл одного из трех видов (относительно новой переменной
(выражение в скобках, выделенного квадрата),получим интеграл одного из трех видов (относительно новой переменной 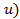 :
: 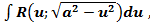

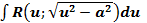 , после чего делаем соответствующие тригонометрические замены:
, после чего делаем соответствующие тригонометрические замены: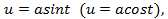

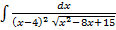
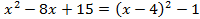 .Сделав подстановку
.Сделав подстановку 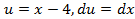 имеем:
имеем: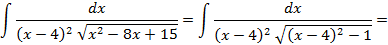
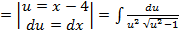 ;
; , где
, где 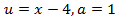 ,следовательно интеграл рационализируется с помощью подстановки
,следовательно интеграл рационализируется с помощью подстановки  :
: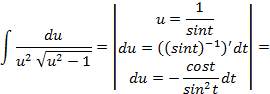
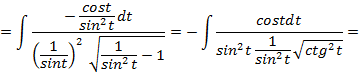
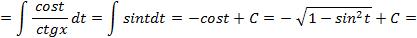
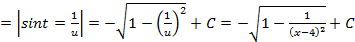 .
.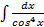 .
.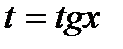 , а применив искусственный прием:
, а применив искусственный прием: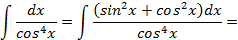
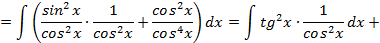

 .
.
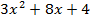 является производной знаменателя
является производной знаменателя 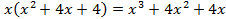 , легко получить табличный интеграл:
, легко получить табличный интеграл: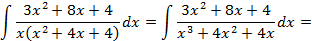
 .
.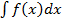 берется (вычисляется),если интеграл выражается через элементарные функции. Если интеграл не выражается через элементарные функции,то интеграл не берется (или его нельзя найти).
берется (вычисляется),если интеграл выражается через элементарные функции. Если интеграл не выражается через элементарные функции,то интеграл не берется (или его нельзя найти).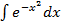 - интеграл Пуассона;
- интеграл Пуассона;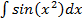 ,
,  - интегралы Френеля;
- интегралы Френеля;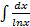 - интегральный логарифм;
- интегральный логарифм;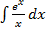 - приводится к интегральному логарифму;
- приводится к интегральному логарифму;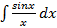 ,
, 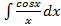 - интегральный синус и косинус соответственно.
- интегральный синус и косинус соответственно.


